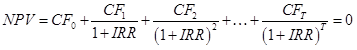湖南省第6届程序大赛第5题 内部收益率

题目E

内部收益率

 

在金融中，我们有时会用内部收益率IRR来评价项目的投资财务效益，它等于使得投资净现值NPV等于0的贴现率。换句话说，给定项目的期数T、初始现金流CF₀和项目各期的现金流CF₁, CF₂, ...，CF_T，IRR是下面方程的解：

 

                       

 

为了简单起见，本题假定：除了项目启动时有一笔投入（即初始现金流CF₀ < 0）之外，其余各期均能赚钱（即对于所有i=1,2,...,T，CF_i> 0）。根据定义，IRR可以是负数，但不能大于-1。

 

 

输入

输入文件最多包含25组测试数据，每个数据占两行，第一行包含一个正整数T（1<=T<=10），表示项目的期数。第二行包含T+1个整数：CF₀, CF₁, CF₂, ..., CF_T，其中CF₀< 0, 0 < CF_i< 10000 (i=1,2,...,T)。T=0表示输入结束，你的程序不应当处理这一行。

 

输出

对于每组数据，输出仅一行，即项目的IRR，四舍五入保留小数点后两位。如果IRR不存在，输出"No"，如果有多个不同IRR满足条件，输出"Too many"（均不含引号）

 

样例输入	样例输出
1 -1 2 2 -8 6 9 0	1.00 0.50

 第一次看到这个题目的时候被最后一句话吓到了，我不知道怎么判断是否有多个不同的IRR可以满足条件。但是当我仔细去看那一个公式，发现那是一个单调的公式，根本就不可能会存在多个不同的IRR满足条件。题目要求保留2位小数，根据题意可以知道IRR在-1到1e6之间。从头到尾的去求时间肯定不够，但是这公式是单调的，这时候我们应该想到的是2分查找。这样的话我们的时间就成了log₂1e6

 1 #include 
 2 #include 
 3 #include<string.h>
 4 #include
 5 using namespace std;
 6 int main()
 7 {
 8     int n,cf[20];
 9     while(~scanf("%d", &n),n)
10     {
11         for(int i = 0; i <= n; i++) scanf("%d", &cf[i]);
12         double l = -1.0, r = 1e6, m;
13         for(int i = 0; i < 100; i++)//这里可以使用eps精确度代替
14         {
15             m = l + (r-l)/2;
16             double f = 1.0, s = 0;
17             for(int j = 1; j <= n; j++)
18             {
19                 f /= (1+m);
20                 s += cf[j]*f;
21             }
22             if(s < -cf[0]) r = m;
23             else l = m;
24         }
25         printf("%.2lf\n", m);
26     }
27     return 0;
28 }