一、树
1、什么是数
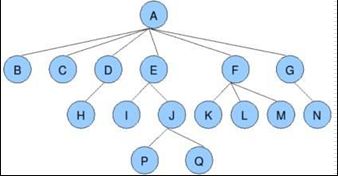
树状图是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个节点有零个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树;
树(tree)是包含n(n>0)个结点的有穷集,其中:
(1)每个元素称为结点(node);
(2)有一个特定的结点被称为根结点或树根(root)。
(3)除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)。
2、相关术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
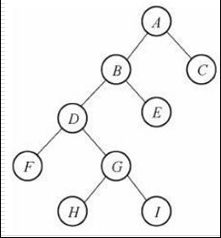
二、二叉树
1、什么是二叉树
二叉树,就是度不差过2的树(节点最多有两个叉)
- 一颗子树最少要包含一个跟节点
- 一个完成的二叉树是由多个子树构成
- 一个子树的子节点也可以表示另一个子树的根节点
三、两种特殊的二叉树
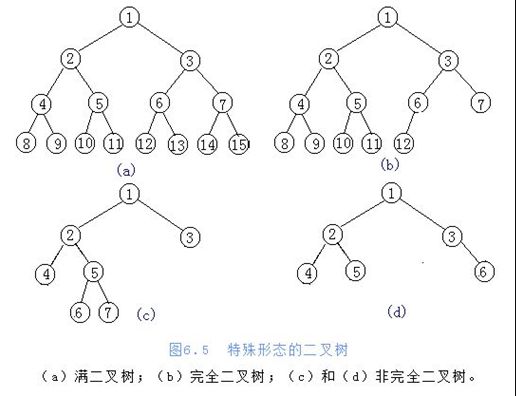
1、满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
2、完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树
四、二叉树的存储方式
1、链式存储方式
a、二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
b、节点定义
class Node():
def __init__(self,item):
self.item = item
self.left = None
self.right = Nonec、二叉树的遍历:
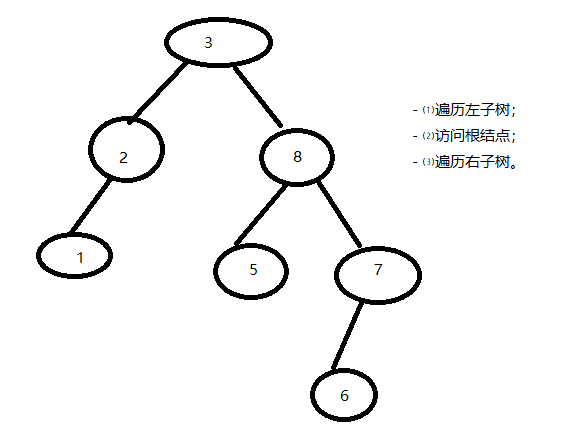
I 、先(前)序遍历:访问根结点的操作发生在遍历其左右子树之前
具体操作:若二叉树非空,则依次执行如下操作:
- ⑴ 访问根结点;
- ⑵ 遍历左子树;
- ⑶ 遍历右子树。
II、中序遍历:访问根结点的操作发生在遍历其左右子树之中(间)。
具体操作: 若二叉树非空,则依次执行如下操作:
- ⑴遍历左子树;
- ⑵访问根结点;
- ⑶遍历右子树。
III、后序遍历:访问根结点的操作发生在遍历其左右子树之后。
若二叉树非空,则依次执行如下操作:
- ⑴遍历左子树;
- ⑵遍历右子树;
- ⑶访问根结点。
IV、层次遍历
用一个队列保存被访问的当前节点的左右孩子以实现层序遍历。
二叉树的遍历代码如下
# 创建节点
class Node():
def __init__(self,item):
self.item = item
self.left = None
self.right = None
class Tree():
#构建一颗空树
def __init__(self):
self.root = None
def add(self,item):
if self.root == None:#向空树中插入第一个节点
node = Node(item)
self.root = node
return
#向非空的二叉树中插入节点
node = Node(item)
cur = self.root
queue = [cur]
while queue:
root = queue.pop(0)
if root.left != None:
queue.append(root.left)
else:
root.left = node
break
if root.right != None:
queue.append(root.right)
else:
root.right = node
break
def travel(self):
cur = self.root
queue = [cur]
if self.root == None:
print('')
return
while queue:
root = queue.pop(0)
print(root.item)
if root.left != None:
queue.append(root.left)
if root.right != None:
queue.append(root.right)
#深度遍历
def forward(self,root):
'''前序遍历(根左右)'''
if root == None:
return
print(root.item)
self.forward(root.left)
self.forward(root.right)
def middle(self,root):
'''中序遍历(左根右)'''
if root == None:
return
self.middle(root.left)
print(root.item)
self.middle(root.right)
def back(self,root):
'''后序遍历(左右根)'''
if root == None:
return
self.back(root.left)
self.back(root.right)
print(root.item)
# 创建二叉树
tree = Tree()
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
# 查看前序遍历结果
tree.forward(tree.root)# 124536
# 查看中序遍历结果
tree.middle(tree.root)#425163
# 查看后序遍历结果
tree.back(tree.root)# 4526312、排序二叉树
二叉树排序一般用中序遍历
代码实现
class SortTree():
def __init__(self):
self.root = None
def add(self,item):
node = Node(item)
cur = self.root
# 如果树没有节点
if self.root == None:
#则开始节点为 创建的节点
self.root = node
return
while True:
#插入节点的值小于根节点的值:往根节点的左侧插
if node.item < cur.item:
if cur.left == None:
cur.left = node
break
else:
cur = cur.left
else:#插入的节点的值大于跟节点:往根节点的右侧插
if cur.right == None:
cur.right = node
break
else:
cur = cur.right
def middle(self,root):
# 如果树没有节点就返回空
if root == None:
return
self.middle(root.left)
print(root.item)
self.middle(root.right)
tree = SortTree()
alist = [3,8,5,7,6,2,1]
for i in alist:
tree.add(i)
tree.middle(tree.root)
# 结果为: 1 2 3 4 5 6 7 8