贪心算法
贪心算法是动态规划算法的一种特殊情况。它并不从整体最优上进行考虑，所做的只是当前看来是最好的选择。当然，我们希望贪心算法得到的最终结果也是整体最优的。
不过，贪心算法并不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须无后效性（不可以回溯），即某个状态以前的过程不会影响以后的状态，只与当前的状态有关。
***
贪心算法的基本要素
最优子结构性质
和动态规划一样，只有具有最优子结构性质的问题才能使用贪心算法。当一个问题的最优解包含了其子问题的最优解，这个问题就具有最优子结构。
贪心选择性质
所求问题的整体最优解可以通过一系列局部最优的选择，及贪心选择来达到。
贪心算法存在的问题
- 不能保证所有求出来的解都是最佳的
- 不能用来求最大最小值问题
- 只能满足部分可行的问题
贪心算法的设计步骤
- 建立数学模型
- 将问题分解为若干个子问题
- 对每一个子问题求解，得到子问题的局部最优解
合并子问题的解，得到问题的整体最优解
***经典例题
汽车加油问题
题目：
解析：
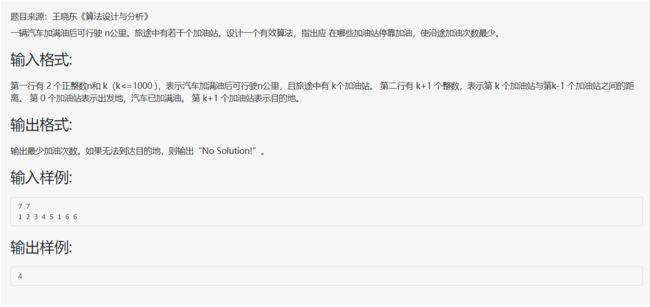
这道题的贪心策略是找到汽车加满油量时可以行驶到的最后一个加油站，在此加油站加满油之后继续前进。假如其中有两个加油站之间的距离大于汽车满油时可以行驶的路程，就输出“No Solution！”。
代码如下：
#include
using namespace std;
#define MAX 1005
int counter; // 记录最少加油次数
int distances[MAX]; // 记录加油站之间的距离
int canDrive; // 一次加油可以行驶的距离
int num; // 加油站个数
void lessCount() {
int sum = 0;
// 假如有一个路程大于汽车满油可以行驶的路程，即无解
for (int i = 0; i <= num; i++) {
if (distances[i] > canDrive) {
cout << "No Solution!" << endl;
return;
}
}
for (int i = 0; i <=num; i++) {
sum += distances[i];
if (sum > canDrive) {
// 加油次数加一
counter++;
// 加油
sum = distances[i];
}
}
cout << counter << endl;
};
int main() {
cin >> canDrive >> num;
for (int i = 0; i <= num; i++) {
cin >> distances[i];
}
lessCount();
system("pause");
return 0;
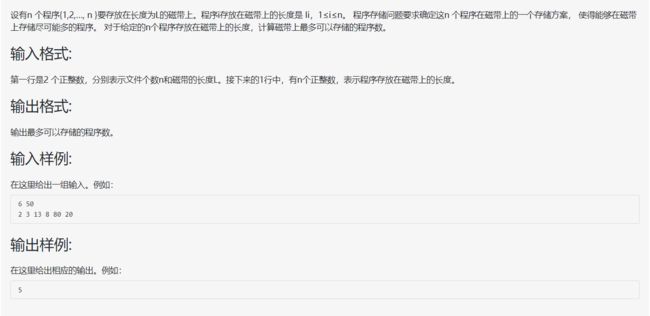
} 程序存储问题
题目：
解析：
这道题思路非常简单，就是选取最小的那几个程序放到磁盘里面，直到放不下为止。用贪心算法的思路来说，就是每个子问题都选取当前最小的程序，最终会得到整体的最优解。
由于使用sort函数，该算法的时间复杂度为O（nlogn）；由于没有开辟新空间，所以空间复杂度为O（1）。
具体代码如下：
#include
#include
using namespace std;
#define MAXLENGTH 1005
int program[MAXLENGTH];
int main() {
int num; // 文件个数
int length; // 磁带长度
int sum = 0; // 可存的程序的长度
int counter = 0; // 计数器
cin >> num >> length;
for (int i = 0; i < num; i++) {
cin >> program[i];
};
sort(program, program + num);
for (int i = 0; i < num; i++) {
sum += program[i];
if (sum <= length) {
counter++;
}
else {
break;
}
}
cout << counter << endl;
system("pause");
return 0;
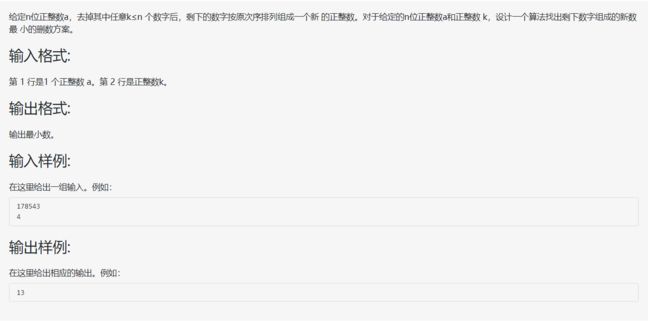
} 删数问题
题目如下：
解析：
拿到题的时候，应该第一反应是删除这行数字中最大的一个。比如样例：
- 178543中删去最大的一个，即8，剩下的数字为17543；
- 17543中删去最大的一个，即7，剩下的数字为1543；
- 1543中删去最大的一个，即5，剩下的数字为143；
····
以此类推，我们可以发现：每次删除的数，都是从第一个数字开始的升序序列的最后一个数！
这样我们的贪心策略就可以变成：每次从第一个数字开始，删去当前的升序序列的最大一个数，一直删到规定的k个数为止。这样，就可以算是由当前的最优解得到最后的最优解。
具体代码如下：
#include
#include
using namespace std;
int main() {
string s;
int num;// 删除的数字个数
cin >> s >> num;
while (num > 0) {
for (int i = 0; i < s.size(); i++) {
if (s[i] > s[i + 1]) {
s.erase(i, 1);
break;
}
}
num--;
};
//除去前导0
for (int i = 0; i < s.size(); i++) {
if (s[0] == '0') {
s.erase(0, 1);
}
}
cout << s << endl;
system("pause");
return 0;
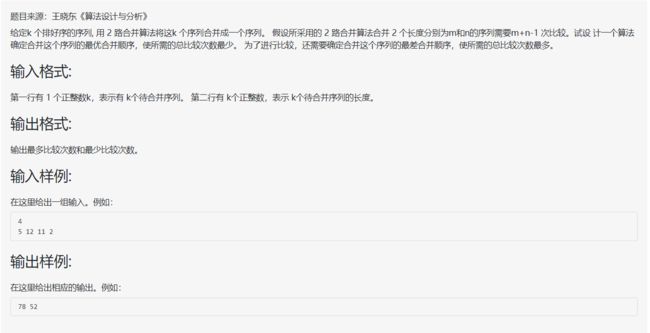
} 最优合并问题
题目如下：
解析：
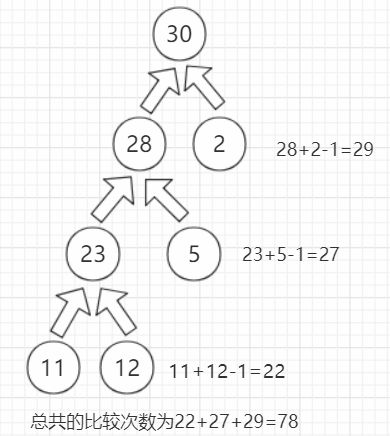
这道题的贪心策略就是每次选取最小/最大的两个数字，从而得到最小/最大的比较次数。
由题意可知，其实是一个哈夫曼树问题：
合并最小的节点，可以获得最小的合并比较次数：
合并最大的节点，可以获得最大的合并比较次数：
具体代码如下：
（实现时使用了stl的优先队列，非常方便）：
#include
#include
using namespace std;
priority_queue q1; // 从大到小的优先队列
priority_queue, greater > q2; // 从小到大的优先队列
int main() {
int num;
int arr[1005];
cin >> num;
int maxtime = 0;
int mintime = 0;
for (int i = 0; i < num; i++) {
cin >> arr[i];
q1.push(arr[i]);
q2.push(arr[i]);
}
// 求出最大的比较次数
while (true) {
if (q1.size() == 1) {
break;
}
else {
int tmp1 = q1.top();
q1.pop();
int tmp2 = q1.top();
q1.pop();
maxtime += tmp1 + tmp2 - 1;
q1.push(tmp1+tmp2);
}
}
// 求出最小的比较次数
while (true) {
if (q2.size() == 1) {
break;
}
else {
int tmp1 = q2.top();
q2.pop();
int tmp2 = q2.top();
q2.pop();
mintime += tmp1 + tmp2 - 1;
q2.push(tmp1+tmp2);
}
}
cout << maxtime << " " << mintime << endl;
system("pause");
return 0;
} 总结：
- 贪婪算法指的是在求解每一步的过程中，都选取当前的最优值
- 贪婪算法并不一定会得到最优的解，但与最优解可以十分接近
- 贪婪算法没有具体的框架
- 问题必须具有无后效性才可以使用贪婪算法得到最优解
结对编程小结
在这次结对编程中和队友依旧配合良好，在我提供了思路或者WA的时候会及时帮我纠正问题所在，以及在最后一题中提出使用优先队列的做法，使代码变得整洁，快速得出了我们所要的答案。谢谢队友再次带飞我。