来手撸一个小小小小小"3D引擎"

开始的唠叨

说是3D引擎确实有点过于博眼球了，其实就是实现了一个透视投影，当然也不是那么简单的。 此篇文章是纯粹给小白看的 高手请勿喷 。也称之为小向带你图形学入门基础 。 哇哈哈哈哈 一说到做一个3D画面的东东 一说总是到DirectX  OpenGL 这些玩意儿 我们这些菜鸟总是 想到哇擦擦 哇C++的   哇 计算机图形学好难。这玩意儿难度好大。其实就那么回事儿 ，DirectX OpenGL 只是工具 而已， 只要把原理搞懂了 你看我用low逼的GDI照样给你绘制一个3D物体 可以这样说即使不用GDI 其他任何能划线 画点的东西 ，我在安卓平台上照样给你实现这个效果。不要局限于工具 谁说做3D就只能用DirectX OpenGL了 ，谁说做3D只能用C++了  。

 

顶点数据展现

首先是3D编程中通用的数据展现 那就是顶点组成的网格数据 称之为mesh， 3个点为一组  组成的三角面片数据。三个点顺时针的方向那么 箭头方向为外表面 另一面为内表面 ，在绘制的时候 内表面不可见。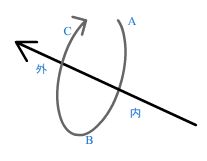

 

好那么我们也以此方式来定义数据 ，我们定义的东西是一个 中心位置在( 0,0，-130)处的立方体。我们的观察点在(0, 0, 0)处 正对着立方体观察。 由于我们想让立方体一个面的颜色相同，所以是两个为一组定义的 ，当然三角形也是以同样的 两个为一组 组成一个正方形面。由此对物体表面空间点的描述数据就做好了。
好 ，定义数据的代码：

 1         public class Marsh
 2         {
 3             public List points;
 4             public Marsh()
 5             {
 6                 points = new List();
 7 
 8                 //0
 9                 Point3dF pointA = new Point3dF(30, 30, -160);
10                 //1
11                 Point3dF pointB = new Point3dF(-30, 30, -160);
12                 //2
13                 Point3dF pointC = new Point3dF(-30, -30, -160);
14                 //3
15                 Point3dF pointD = new Point3dF(30, -30, -160);
16                 //4
17                 Point3dF pointE = new Point3dF(30, 30, -100);
18                 //5
19                 Point3dF pointF = new Point3dF(-30, 30, -100);
20                 //6
21                 Point3dF pointG = new Point3dF(-30, -30, -100);
22                 //7
23                 Point3dF pointH = new Point3dF(30, -30, -100);
24 
25                 points.Add(pointA);
26                 points.Add(pointB);
27                 points.Add(pointC);
28                 points.Add(pointD);
29 
30                 points.Add(pointE);
31                 points.Add(pointF);
32                 points.Add(pointG);
33                 points.Add(pointH);
34 
35                 
36 
37                 path1 = new List<int>() { 
38                     4, 6,7,
39                     4,5,6,
40                     5 ,2 ,6,
41                     5, 1, 2,
42                     1 ,3 ,2,
43                     1, 0 ,3,
44                     0 ,7 ,3,
45                     0 ,4, 7
46                     ,
47                     4, 1, 5,
48                     4 ,0 ,1,
49                     6, 2 ,7,
50                     2, 3, 7
51                 };
52 
53                 faceColors = new List();
54                 Random rdm = new Random();
55 
56                 for (int i = 0; i < 6; i++)
57                 {
58                     Brush b= new SolidBrush(Color.FromArgb(rdm.Next(0, 255), rdm.Next(0, 255), rdm.Next(0, 255)));
59                     //Brush b = new SolidBrush(Color.FromArgb(266 / 6 * i, 266 / 6 * i, 266 / 6 * i));
60                     faceColors.Add(b);
61                     faceColors.Add(b);
62                 }
63                 
64             }
65             public List faceColors;
66             public List<int> path1;
67 
68         }

 

关于透视投影 和顶点绘制

我数学底子差 在写这个例子之前参考了很多前辈的 图形学理论基础。最主要是透视投影 和3D旋转矩阵绕任意轴旋转 。甚至没完全搞懂 于是我就抄起代码开搞了。 不得不说这玩意儿真的很有意思。
首先是透视投影：http://blog.csdn.net/popy007/article/details/1797121
作者讲的很详细 其实我只看到一半 ，后面矩阵推导那些太难了 没有继续往下啃 。视线是一个发散的方式从一个点出去 （其实最后发现不用管什么视椎体不视椎体的）。 假设视点前面有一张半透明的纸张 视线上的点是怎么打到纸张上的？关于这个问题  你要粗暴点确实很简单 就是三角形 初中的知识。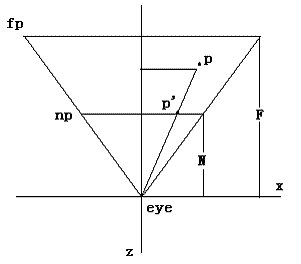

就如开始所述 视点在(0,0,0) 处看向 位于(0,0,-130) 的立方体  ，假设有一架摄像机  ，那么上图就是他的从空中看下去的俯视图。设p为(x,z)　　p'为(x' ,z') 。则x'=-N(x/z)  y'=-N(y/z)。为了方便 我们的数据定义也是跟示意图上差不多的。于是我们依葫芦画瓢 把所有的点绘制出来 包装成一个paint函数。
需要注意的是平面坐标系 跟屏幕坐标之间的转换 ，其实不难 你其他计算应用数学公式 数学函数 还是一样该咋算咋算。  完成后我们平面坐标系的0,0  对应屏幕坐标的0,0   。

看到没 x轴0左边也是负数 不用管  就只是y的符号不一样 变成-y就可以了。然后要让他显示在窗口中间  还要进行偏移 就是x加偏移， y加偏移  就这样就完成啦 。  哈哈哈哈哈。 

 1         public void paint()
 2         {
 3             Graphics gph = Graphics.FromHwnd(this.Handle);
 4             gph.Clear(Color.Lavender);
 5             //进行到屏幕坐标的映射(x y z)
 6             //p~ =(-n x/z       -n y/z      -n)
 7             PointF screenLastPoint= PointF.Empty;
 8             for (int i = 0; i < msh.path1.Count / 3; i++)
 9             {
10                 //if (i >= 4)
11                 //    return;
12                 PointF screenPointA = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3]].x / msh.points[msh.path1[i * 3]].z)) , (float)((-nearPlan) * (msh.points[msh.path1[i * 3]].y / msh.points[msh.path1[i * 3]].z))  );
13                 PointF screenPointB = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 1]].x / msh.points[msh.path1[i * 3 + 1]].z)) , (float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 1]].y / msh.points[msh.path1[i * 3 + 1]].z))  );
14                 PointF screenPointC = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 2]].x / msh.points[msh.path1[i * 3 + 2]].z))  , (float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 2]].y / msh.points[msh.path1[i * 3 + 2]].z))  );
15 
16                 screenPointA.Y = -screenPointA.Y;
17                 screenPointB.Y = -screenPointB.Y;
18                 screenPointC.Y = -screenPointC.Y;
19 
20                 screenPointA.Y=screenPointA.Y+offsety;
21                 screenPointB.Y= screenPointB.Y+offsety;
22                 screenPointC.Y = screenPointC.Y + offsety;
23 
24                 screenPointA.X = screenPointA.X + offsetx;
25                 screenPointB.X = screenPointB.X + offsetx;
26                 screenPointC.X = screenPointC.X + offsetx;
27 
28                 System.Drawing.Drawing2D.GraphicsPath ph = new System.Drawing.Drawing2D.GraphicsPath(
29                     new PointF[] { screenPointA, screenPointB, screenPointC },
30                     new byte[] { 1, 1, 1 },
31                     System.Drawing.Drawing2D.FillMode.Winding);
32 
33 
34                 //---求法向量及夹角 如果为true 则渲染面//计算当前管线三角面片的法向量 是否朝着镜头 ，最终决定是否可见
35                 if (angelCalc(msh.points[msh.path1[i * 3]], msh.points[msh.path1[i * 3+1]], msh.points[msh.path1[i * 3+2]]) == true)
36                     gph.FillPath(msh.faceColors[i], ph);
37             }
38 
39             //绘制边框
40             gph.DrawLine(Pens.Red, new PointF(offsetx - 36, offsety - 36), new PointF(offsetx + 36, offsety - 36));
41             gph.DrawLine(Pens.Red,  new PointF(offsetx + 36, offsety - 36),new PointF(offsetx + 36, offsety + 36));
42             gph.DrawLine(Pens.Red, new PointF(offsetx + 36, offsety +36), new PointF(offsetx - 36, offsety + 36));
43             gph.DrawLine(Pens.Red, new PointF(offsetx - 36, offsety + 36), new PointF(offsetx - 36, offsety - 36));
44 
45             ////绘制网格线
46             //screenLastPoint = PointF.Empty;
47             //for (int i = 0; i < msh.path1.Count / 3; i++)
48             //{
49             //    //if (i >= 4)
50             //    //    return;
51             //    PointF screenPointA = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3]].x / msh.points[msh.path1[i * 3]].z)), (float)((-nearPlan) * (msh.points[msh.path1[i * 3]].y / msh.points[msh.path1[i * 3]].z)));
52             //    PointF screenPointB = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 1]].x / msh.points[msh.path1[i * 3 + 1]].z)), (float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 1]].y / msh.points[msh.path1[i * 3 + 1]].z)));
53             //    PointF screenPointC = new PointF((float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 2]].x / msh.points[msh.path1[i * 3 + 2]].z)), (float)((-nearPlan) * (msh.points[msh.path1[i * 3 + 2]].y / msh.points[msh.path1[i * 3 + 2]].z)));
54 
55             //    screenPointA.Y = -screenPointA.Y;
56             //    screenPointB.Y = -screenPointB.Y;
57             //    screenPointC.Y = -screenPointC.Y;
58 
59             //    screenPointA.Y = screenPointA.Y + offsety;
60             //    screenPointB.Y = screenPointB.Y + offsety;
61             //    screenPointC.Y = screenPointC.Y + offsety;
62 
63             //    screenPointA.X = screenPointA.X + offsetx;
64             //    screenPointB.X = screenPointB.X + offsetx;
65             //    screenPointC.X = screenPointC.X + offsetx;
66 
67             //    gph.DrawLine(Pens.Red, screenPointA, screenPointB);
68             //    gph.DrawLine(Pens.Red, screenPointB, screenPointC);
69             //    gph.DrawLine(Pens.Red, screenPointC, screenPointA);
70 
71             //}
72 
73         }

  

绕着坐标轴进行旋转  

最开始我没有绘制面只是绘制的顶点线框而已 。然后我想做的是旋转  让他转起来，总共八个点连成线就是立方体了，哪怕是low逼的线条 只要转起来是不是就有立方体的样子了。  哇哈哈哈哈。最开始我想的很简单啊 立体的旋转也没啥不得了的啊 ，比如饶y轴旋转 我把他当成平面的不就得了么 y不变x和z变。 绕x轴旋转 同理。 我原来也写过平面的点进行旋转的计算。 为了符合图形学上的标准方式 最后我还是使用二维矩阵旋转的方式： 

 1         public void RotationTest2()
 2         {
 3 
 4             //二维空间旋转矩阵为 ： x是角度
 5             //cos(x)  -sin(x)   (1-cos(x))tx+ty*sin(x))  x
 6             //Sin(x) cos(x)     (1-cos(x))ty-tx*sin(x)) y
 7 
 8             //2pi 等于360度
 9             //绕y轴旋转
10             //double xita = ((Math.PI * 2d) / 360d) * 2d;
11             double xita = ((Math.PI * 2d) / 360d) * anglex;
12             double cosx = Math.Cos(xita);
13             double sinx = Math.Sin(xita);
14 
15             double xitay = ((Math.PI * 2d) / 360) * angley;
16             double cosy = Math.Cos(xitay);
17             double siny = Math.Sin(xitay);
18 
19             for (int i = 0; i < msh.points.Count; i++)
20             {
21                 //Point3dF tmpPoint = new Point3dF(msh.points[i].x, msh.points[i].y, msh.points[i].z);
22                 Point3dF tmpPoint = new Point3dF(mshSource.points[i].x, mshSource.points[i].y, mshSource.points[i].z);
23                 msh.points[i].x =
24                     tmpPoint.x * cosx + ((-sinx) * tmpPoint.z) +
25                 (((1d - cosx) * 0d) + ((-130d) * sinx));
26 
27                 msh.points[i].z =
28                     tmpPoint.x * sinx + (cosx * tmpPoint.z) +
29                     (((1d - cosx) * (-130d)) - ((0d) * sinx));
30 
31                 msh.points[i].y = tmpPoint.y;
32 
33                 //---------------------------------
34                 tmpPoint = new Point3dF(msh.points[i].x, msh.points[i].y, msh.points[i].z);
35 
36                 msh.points[i].y = tmpPoint.y * cosy + ((-siny) * tmpPoint.z) +
37                 (((1d - cosy) * 0d) + ((-130d) * siny));
38 
39                 msh.points[i].z = tmpPoint.y * siny + (cosy * tmpPoint.z) +
40                     (((1d - cosy) * (-130d)) - ((0d) * siny));
41             }
42 
43         }

 

 

注意了 绕着任意轴进行旋转

现在我想做的是做一个跟踪球效果 。鼠标按下拖动的时候让物体 像烤肉串样绕着一根轴旋转。 网上跟踪球都是旋转相机 我们这里直接旋转物体坐标。绕着任意轴旋转啊绕着任意轴旋转的矩阵 说实话 3D旋转矩阵这个我搞不懂 ，我看不懂推导过程 但是我会看公式 哇哈哈哈哈。
https://www.cnblogs.com/graphics/archive/2012/08/10/2627458.html
其他的博文里贴出来的旋转矩阵也是这样 直接把他的代码抄下来之  ，c++的 我抄成c#的 没啥难的 我已经超过好些c++代码了。总之我们要做的就是 得出一个二维数组作为矩阵回传 让所有坐标根据此矩阵进行运算。注意有两个基本概念：  两个点相减 a-b  得出的是 b到a 的向量 (0,0) -(1,1)  =(-1,-1)  ，然后是向量归一化： 什么叫归一化， 就是 把向量的方向不变 长度变到单位长度 ，也就是1。问向量归一化怎么搞  。好 ，比如一个二维向量，计算原理就是通过距离计算公式得出距离。这个距离与1的比值等于 现x与归一化后x的比值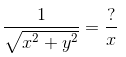：求归一化后y的值同理。当然这些都是基础的没什么特别说的。
求旋转矩阵的函数：

 1         //得到旋转矩阵
 2         double[,] RotateArbitraryLine(Point3dF v1, Point3dF v2, double theta)
 3         {
 4             
 5             double a = v1.x;
 6             double b = v1.y;
 7             double c = v1.z;
 8             Point3dF p = new Point3dF(v2.x - v1.x, v2.y - v1.y, v2.z - v1.z);
 9             //v2归一化
10             double x_p2 = p.x / Math.Sqrt(Math.Pow(p.x, 2) + Math.Pow(p.y, 2));
11             double y_p2 = p.y / Math.Sqrt(Math.Pow(p.x, 2) + Math.Pow(p.y, 2));
12 
13             if (double.IsNaN(x_p2))
14                 x_p2 = 0;
15             if (double.IsNaN(y_p2))
16                 y_p2 = 0;
17 
18             double u = x_p2;
19             double v = y_p2;
20             double w = 0d;// -130d;// 0d;
21 
22             double uu = u * u;
23             double uv = u * v;
24             double uw = u * w;
25             double vv = v * v;
26             double vw = v * w;
27             double ww = w * w;
28             double au = a * u;
29             double av = a * v;
30             double aw = a * w;
31             double bu = b * u;
32             double bv = b * v;
33             double bw = b * w;
34             double cu = c * u;
35             double cv = c * v;
36             double cw = c * w;
37 
38             double costheta = Math.Cos(theta);
39             double sintheta = Math.Sin(theta) ;
40             double[,] pOut = new double[4, 4];
41             pOut[0,0] = uu + (vv + ww) * costheta;
42             pOut[1,0] = uv * (1 - costheta) + w * sintheta;
43             pOut[2,0] = uw * (1 - costheta) - v * sintheta;
44             pOut[3,0] = 0;
45                   
46             pOut[0,1] = uv * (1 - costheta) - w * sintheta;
47             pOut[1,1] = vv + (uu + ww) * costheta;
48             pOut[2,1] = vw * (1 - costheta) + u * sintheta;
49             pOut[3,1] = 0;
50                   
51             pOut[0,2] = uw * (1 - costheta) + v * sintheta;
52             pOut[1,2] = vw * (1 - costheta) - u * sintheta;
53             pOut[2,2] = ww + (uu + vv) * costheta;
54             pOut[3,2] = 0;
55                   
56             pOut[0,3] = (a * (vv + ww) - u * (bv + cw)) * (1 - costheta) + (bw - cv) * sintheta;
57             pOut[1,3] = (b * (uu + ww) - v * (au + cw)) * (1 - costheta) + (cu - aw) * sintheta;
58             pOut[2,3] = (c * (uu + vv) - w * (au + bv)) * (1 - costheta) + (av - bu) * sintheta;
59             pOut[3,3] = 1;
60 
61             return pOut;
62         }

 

函数写好了 矩阵也能得出了，还有个问题：函数的那几个参数 ，旋转的度数也好搞 按下的时候记录一个点 拖动的时候计算跟他的距离 距离作为度数 拖动50像素 旋转50度。 旋转的那根儿轴你怎么得出来，开始点容易 立方体的中心是0 0 -130  。按下的时候记录了按下开始点 鼠标的移动就已经是一个向量了 所以我们只需要对这个向量 绕z轴进行90度旋转 ，z也设成-130 就跟中心点平齐了 就是需要的烤肉串儿的旋转轴了。 好 原理讲完了 ，代码走起：

 1         private void Form1_MouseMove(object sender, MouseEventArgs e)
 2         {
 3             //必须要得出旋转的轴才行
 4             if (pressed)
 5             {
 6 
 7                 //中心点 0,0,-130
 8                 //通过拖动远近决定旋转角度，垂直向量 得到旋转轴
 9 
10                 //得出鼠标拖动向量 
11 
12                 Point3dF dragJuli = new Point3dF((e.Location.X - startPoint.X),( e.Location.Y - startPoint.Y),-130d);
13                 //还要旋转90度才是真正的旋转轴
14                 //cos(x)  -sin(x)
15                 //Sin(x) cos(x)  
16                 double cos90=0d;
17                 double sin90=1d;
18                 var x = dragJuli.x * 0d + dragJuli.y * 1d;
19                 var y = dragJuli.x * 1d + dragJuli.y * 0d;
20 
21                 Point3dF dragJuli2 = new Point3dF(x, y, dragJuli.z);
22 
23                 //Point3dF dragJuli90=
24                 //x1 x2+y1 y2=0
25                 //double x2=(-dragJuli.y)/(dragJuli.x);
26                 //垂直的旋转轴向量
27                 //Point3dF roll = new Point3dF(x2, 1, -130);
28 
29                 //拖动距离 拖动距离等于角度
30                 angelourua= Math.Sqrt(Math.Pow((e.Location.X - startPoint.X), 2) + Math.Pow((e.Location.Y - startPoint.Y), 2));
31                 angelourua = angelourua % 360;
32                 angelourua = ((Math.PI * 2d) / 360d) * angelourua;
33 
34                 double[,] roatMatarix= RotateArbitraryLine(new Point3dF(0, 0, -130d), dragJuli2,angelourua);
35 
36                 RotationTest(roatMatarix);
37                 paint();
38 
39             }
40         }

 

好就这样 先进行3d空间的点旋转， 再进行平面坐标映射绘制 用线连起来。是不是就有点3D立体的样子了。哇哈哈哈哈

 注意了 面绘制

前面的都是有些挖的别人的，这个功能绝对是自己捣鼓出来的。开始那些不论是两两之间的线条绘制啥的都只能算是 点绘制  ，我们现在要进行面绘制。首先你要清楚的是我的顶点三角面片数据已经给出了， 3d坐标点打在半透明纸张上 的x，y 也已经得出了。 调用gdi的fillpath按ABC 的顺序连起来 就能绘制一个三角面片 是不是很简单。但是先别慌 还有两个问题需要处理，一个就是可见面判别。 就是两个三角面片 的位置 决定了 在透视投影的时候哪个在前哪个在后， 还有面相交的情况呢 ？ 是不是很复杂？其实根本不用管，即使要管 只要你使用z缓冲算法 也不是很复杂 zbuffer 。就是在求出屏幕x y过后把同xy的点z越靠近视点的放在前面 这样就达到目的了。这里我们先 不管这个zbuffer算法  下次有空闲了我们再来写。这里我们使用另外一种方式 通过判别正向面与后向面来达到目的。前面我们不是说了吗 ：


我们通过计算每个三角面片的法向量， 然后我们有一个视点到三角面片的向量 ，通过计算两向量的点积  然后通过反余弦函数就可以得出两向量的夹角 。 如果夹角大于90度代表三角面片正向面朝着视点， 如果小于90度代表正向面背对了视点， 则不对这个三角面片进行渲染。如此一来 你仔细想想 我们的立方体至始至终不会存在一个面把另一个面遮挡的情况。
好了原理讲至此 好下面 根据原理撸代码：

 1         //平面是否面向摄像机的判别
 2         public bool angelCalc( Point3dF A,Point3dF B,Point3dF C)
 3         {
 4             //https://zhidao.baidu.com/question/810216091258785532.html
 5             //AB、AC所在平面的法向量即AB×AC=(a,b,c),其中：
 6             //a=(y2-y1)(z3-z1)-(z2-z1)(y3-y1)
 7             //b=(z2-z1)(x3-x1)-(z3-z1)(x2-x1)
 8             //c=(x2-x1)(y3-y1)-(x3-x1)(y2-y1)
 9             
10             //先得出点 对应的向量
11             //Point3dF AB = new Point3dF(B.x - A.x, B.y - A.y, B.z - A.z);
12 
13             //首先求出法向量
14             double a = ((B.y - A.y)*(C.z - A.z) - (B.z - A.z)*(C.y - A.y));
15             double b = (B.z - A.z) * (C.x - A.x) - (C.z - A.z) * (B.x - A.x);
16             double c = (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
17             Point3dF bb = new Point3dF(a, b, c);
18             //套公式 第二册 下b 39  通过两向量的cos函数 继而通过反余弦得出角度
19             var angelPlan =Math.Acos(
20                 (A.x * bb.x + A.y * bb.y + A.z * bb.z) / (
21                Math.Sqrt(Math.Pow(A.x, 2) + Math.Pow(A.y, 2) + Math.Pow(A.z, 2)) *
22                Math.Sqrt(Math.Pow(bb.x, 2) + Math.Pow(bb.y, 2) + Math.Pow(bb.z, 2))
23                )
24                );
25 
26             if (angelPlan > (Math.PI / 2))//法向量与镜头的夹角大于90度 代表三角面片面向摄像机 则可见
27                 return true;
28             else//否则不可见
29                 return false;
30         }

 

关于光照

光照这玩意儿还是 用到三角面片的法向量 ，三角面片正对着光 则表面亮度最高 ，垂直则变成黑暗。参照面绘制的原理就可以搞出来 我这里就每个面各用些五颜六色的颜色算了吧 懒得整了。

其他的

还有我的摄像机镜头是固定的 ，其实还有很多工作需要做  。 希望各位大大继续完善。看下效果 是不是有模有样：上个gif图：

你可以把平面面向摄像机判别函数返回的值反向一下看看什么效果，是不是看到内壁的那一面了 是不是很神奇哇哈哈哈哈
是的你没看错就这么几百行核心部分就实现了  差不多都是数学知识 ，其他的都是添砖加瓦的事，原理都在这了。 好了 以后再看DirectX 啊OpenGL啊 图形学 变换矩阵啊那些的 别被唬住了 没那么难的。
按说的话这些知识总体来说蛮难的 但是毕竟还是学过高中的向量  两向量垂直时点积等于零 这些之类的  ， 靠着摸着石头过河 把这些半懂不懂的知识 拼凑起来 加上各种度娘 和查资料 来实现 没想到竟然成功了。 意外意外  ，当然学习是要靠自己的  你想直接度娘给你出来个你要的效果 那是不可能的。