https://www.kaggle.com/c/titanic
题目简介
Titanic的沉没是历史上最臭名远扬的沉船事故之一。Titanic在1912年4月15日的处女航中撞上了冰山沉没,造成了全2224名船员中1502名人员死亡。这场骇人听闻的悲剧震惊了国际社会,从而引起了船只安全监管的进步。
导致如此大量死亡的一个原因是船上没有足够的救生艇提供给船员和乘客。虽然在这次沉船中幸存多多少少是由于幸运,但是某些乘客看起来更容幸存下来,比如妇女,儿童,和头登仓的乘客。
在这次挑战中,我们想要你分析出哪种类的人群更容易幸存。尤其是我们希望你能应用机器学习的工具来预测在这场悲剧中哪些乘客得以幸存。
初探数据
import pandas as pd
import numpy as np
df = pd.read_csv("train.csv")
df.info()
Int64Index: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 90.5+ KB
我们从Age, Cabin Embarked等项可以看出数据存在缺失值
df.head()
男女幸存比例统计,可以看出女性幸存比例明显高于男性
df.Sex[df.Survived == 1].value_counts() / df.Sex.value_counts()
female 0.742038
male 0.188908
Name: Sex, dtype: float64
仓等幸存比例统计,可以看出1等仓幸存比列明显高于其他仓等
df.Pclass[df.Survived == 1].value_counts() / df.Pclass.value_counts()
1 0.629630
2 0.472826
3 0.242363
Name: Pclass, dtype: float64
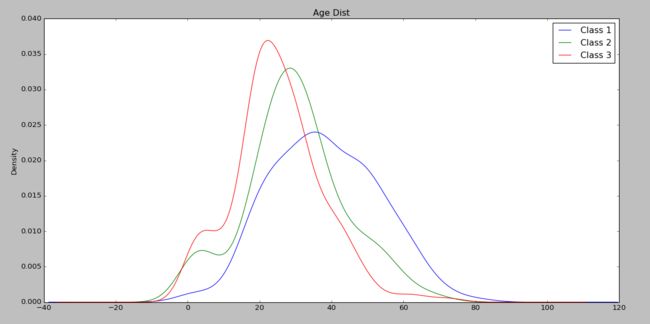
年龄分布,可以看出1等舱的乘客年龄比较大
由此我们推测,性别,仓等都是很重要的特征。
特征处理
由于我们从数据中看到年龄字段有缺失值,题目提示了年龄也是一个比较重要的特征,因此我们先训练一个模型来对年龄做填充。
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.preprocessing import PolynomialFeatures
from sklearn import metrics
def quadratic_transform(X, degree=2):
if degree == 1:
return X
quadratic_featurizer = PolynomialFeatures(degree=degree)
return quadratic_featurizer.fit_transform(X)
def extract_age_feature(df):
dummies_Sex = pd.get_dummies(df['Sex'], prefix= 'Sex')
age_df = df[['Age', 'Sex', 'Parch', 'SibSp', 'Pclass']].copy()
age_df = pd.concat([age_df, dummies_Sex], axis=1)
age_df = age_df.filter(regex='Age|Sex_.*|Parch|SibSp|Pclass')
return age_df
age_df = extract_age_feature(df)
train_data = age_df[age_df.Age.notnull()].as_matrix()
X = train_data[:, 1:]
y = train_data[:, 0]
X_quadratic = quadratic_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_quadratic, y, test_size=0.2, random_state=1)
tuned_parameters = {'n_estimators': [500, 700, 1000], 'max_depth': [None, 1, 2, 3], 'min_samples_split': [1, 2, 3]}
clf = GridSearchCV(RandomForestRegressor(), tuned_parameters, cv=5, n_jobs=-1, verbose=1)
clf.fit(X_train, y_train)
age_rfr = clf.best_estimator_.fit(X_train, y_train)
metrics.mean_absolute_error(y_test, y_pred)
填补缺失的年龄数据
predict_data = age_df[age_df.Age.isnull()].as_matrix()
X_quadratic = quadratic_transform(predict_data[:, 1:])
# 对年龄进行预测
predict_age = age_rfr.predict(X_quadratic)
df.loc[df.Age.isnull(), 'Age'] = predict_age
对原始数据进行特征工程
def feture_extract(df):
processed_df = df.copy()
# 类型特征离散化
dummies_Sex = pd.get_dummies(processed_df['Sex'], prefix= 'Sex')
dummies_Embarked = pd.get_dummies(processed_df['Embarked'], prefix= 'Embarked')
dummies_Pclass = pd.get_dummies(processed_df['Pclass'], prefix= 'Pclass')
# 构造年龄是否小于12岁的特征
age_Greater_12 = processed_df.Age.copy()
age_Greater_12[processed_df.Age >= 12] = 1
age_Greater_12[processed_df.Age < 12] = 0
# 构造是否含有兄弟姐妹的特征
has_SibSp = processed_df.SibSp.copy()
has_SibSp[processed_df.SibSp != 0] = 1
has_SibSp[processed_df.SibSp == 0] = 0
# 构造是否含有父母的特征
has_Parch = processed_df.Parch.copy()
has_Parch[processed_df.Parch != 0] = 1
has_Parch[processed_df.Parch == 0] = 0
processed_df['Age_Greater_12'] = age_Greater_12
processed_df['Has_SibSp'] = has_SibSp
processed_df['Has_Parch'] = has_Parch
processed_df = pd.concat([processed_df, dummies_Embarked, dummies_Pclass, dummies_Sex], axis=1)
scaler = preprocessing.StandardScaler()
# 对年龄进行scale
age_scale_param = scaler.fit(processed_df['Age'])
processed_df['Age_scaled'] = scaler.fit_transform(processed_df['Age'], age_scale_param)
processed_df.drop(['PassengerId', 'Sex', 'Age', 'Embarked', 'Fare','Pclass', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
return processed_df
processed_df = feture_extract(df)
模型训练
train_data = processed_df.as_matrix()
X_train, y_train = train_data[:,1:], train_data[:,0]
# 892x120
X_quadratic_train = quadratic_transform(X_train)
tuned_parameters = [
{'penalty': ['l1'], 'tol': [1e-5, 1e-6], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]},
{'penalty': ['l2'], 'tol': [1e-5, 1e-6], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]},
]
clf = GridSearchCV(LogisticRegression(), tuned_parameters, cv=5, n_jobs=-1, verbose=1)
clf.fit(X_quadratic_train, y_train)
survived_lr = clf.best_estimator_.fit(X_quadratic_train, y_train)
预测
在我们训练完模型之后,就可以使用这个模型对测试集进行预测,当然第一步要做的还是一系列相同的特征工程把原始数据变成模型可以使用的数据
test_df = pd.read_csv("test.csv")
# 抽取年龄特征
age_df = extract_age_feature(test_df[test_df.Age.isnull()])
age_predict_data = age_df.as_matrix()
X_quadratic = quadratic_transform(age_predict_data[:, 1:])
# 填充年龄有确实的数据
test_df.loc[test_df.Age.isnull(), 'Age'] = age_rfr.predict(X_quadratic)
test_processed_df = feture_extract(test_df)
X_test = test_processed_df.as_matrix()
X_quadratic_test = quadratic_transform(X_test)
使用模型进行预测,然后提交结果
y_test = survived_lr.predict(X_quadratic_test)
result = pd.DataFrame({'PassengerId':test_df['PassengerId'].as_matrix(), 'Survived':y_test.astype(np.int32)})
result.to_csv("./logistic_regression_result.csv", index=False)
模型优化
使用的模型只是我们的一个baseline,我们还需要对模型进行优化,比如我们的模型是过拟合还是欠拟合,特征是否显著等。我们先来看下系数的相关性。
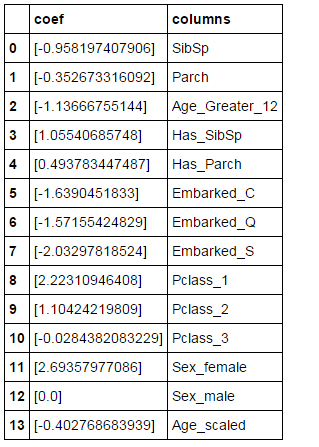
pd.DataFrame({"columns":list(processed_df.columns)[1:], "coef":list(survived_lr.coef_.T)})
由上图可以看出SibSp, Parch, Pclass_1, Pclass_2, Sex_female等特征是正相关。Age_Greater_12是一个负相关的特征,这说明小朋友的幸存率的确会高一些。Embarked的特征都是负相关而且没什么区别,看起来这个特征没有什么。
因此我们先列出一些可以优化的点:
1.将Age进行离散化。
2.去掉Emarked特征。
3.加入Cabin特征,因为救生艇的位置应该还是跟Cabin有关系的。
重新特征工程,加入是否有Cabin,对Age, SibSp, Parch离散化
def feture_extract2(df):
processed_df = df.copy()
# 类型特征离散化
dummies_Sex = pd.get_dummies(processed_df['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(processed_df['Pclass'], prefix= 'Pclass')
# 对年龄进行离散化
age_cut = pd.cut(processed_df.Age, bins=[0,12,24,36,48,60,72,84,96,102])
dummies_Age = pd.get_dummies(age_cut, prefix='Age')
# 兄弟姐妹数量离散化
sibsp_cut = pd.cut(processed_df.SibSp, bins=[0,1,2,3,4,5,6,7,8])
dummies_SibSp = pd.get_dummies(sibsp_cut, prefix='SibSp')
# 构造是否含有兄弟姐妹的特征
has_SibSp = processed_df.SibSp.copy()
has_SibSp[processed_df.SibSp != 0] = 1
has_SibSp[processed_df.SibSp == 0] = 0
# 父母数量离散化
parch_cut = pd.cut(processed_df.Parch, bins=[0,1,2,3])
dummies_Parch = pd.get_dummies(parch_cut, prefix='Parch')
# 构造是否含有父母的特征
has_Parch = processed_df.Parch.copy()
has_Parch[processed_df.Parch != 0] = 1
has_Parch[processed_df.Parch == 0] = 0
has_Cabin = processed_df.Cabin.copy()
has_Cabin[processed_df.Cabin.notnull()] = 1
has_Cabin[processed_df.Cabin.isnull()] = 0
dummies_Cabin = pd.get_dummies(has_Cabin, prefix='Cabin')
processed_df['Has_SibSp'] = has_SibSp
processed_df['Has_Parch'] = has_Parch
processed_df = pd.concat([processed_df, dummies_SibSp, dummies_Parch, dummies_Pclass, dummies_Sex, dummies_Age, dummies_Cabin], axis=1)
processed_df = processed_df.filter(regex='Survived|SibSp_.*|Parch_.*|Age_Greater_12|Has_.*|Cabin_.*|Pclass_.*|Sex_.*|Age_.*')
return processed_df
processed_df = feture_extract2(df)
重新训练模型
train_data = processed_df.as_matrix()
X_data, y_data = train_data[:,1:], train_data[:,0]
# 分割训练集和验证集
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size=0.2, random_state=1)
X_quadratic_train = quadratic_transform(X_train, 1)
X_quadratic_test = quadratic_transform(X_test, 1)
tuned_parameters = [
{'penalty': ['l1'], 'tol': [1e-5, 1e-6], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]},
{'penalty': ['l2'], 'tol': [1e-5, 1e-6], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]},
]
clf = GridSearchCV(LogisticRegression(), tuned_parameters, cv=5, n_jobs=-1, verbose=1)
clf.fit(X_quadratic_train, y_train)
survived_lr = clf.best_estimator_.fit(X_quadratic_train, y_train)
# array([ 0.75675676, 0.66666667, 0.69444444, 0.85714286, 0.82857143])
cross_validation.cross_val_score(survived_lr, X_quadratic_test, y_test, cv=5)
我们不断地做特征工程,产生的特征越来越多,用这些特征去训练模型,会对我们的训练集拟合得越来越好,同时也可能在逐步丧失泛化能力,从而在待预测的数据上,表现不佳,也就是发生过拟合问题。
学习曲线可以帮我们判定我们的模型现在所处的状态。
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, train_sizes=np.linspace(.05, 1., 20), verbose=0, plot=True):
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes, verbose=verbose)
train_scores_mean, train_scores_std = np.mean(train_scores, axis=1), np.std(train_scores, axis=1)
test_scores_mean, test_scores_std = np.mean(test_scores, axis=1), np.std(test_scores, axis=1)
if plot:
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel(u"Sample Num")
plt.ylabel(u"Score")
plt.gca().invert_yaxis()
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="b")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1, color="r")
plt.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"Train Set Score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"Test Set Score")
plt.legend(loc="best")
plt.draw()
plt.show()
plt.gca().invert_yaxis()
midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
return midpoint, diff
plot_learning_curve(survived_lr, "Learning Curve", X_data, y_data)
可以看出来,训练集和交叉验证集上的得分曲线走势还是符合预期的。目前的曲线看来,我们的模型并不处于过拟合的状态(过拟合的表现是训练集上得分高,而交叉验证集上要低很多)。因此我们可以再做些特征工程,添加一些新产出的特征或者组合特征到模型中。
模型融合
模型融合大概就是当我们手头上很多在同一份数据集上训练得到的分类器时,我们让他们都分别去做判定,然后对结果做投票统计,取票数最多的结果为最后结果。
from sklearn.ensemble import BaggingRegressor
train_data = processed_df.as_matrix()
X_data, y_data = train_data[:,1:], train_data[:,0]
X_quadratic_train = quadratic_transform(X_data)
survived_bagging_lr = BaggingRegressor(survived_lr, n_estimators=20,
max_samples=0.8, max_features=1.0, bootstrap=True, bootstrap_features=True, n_jobs=-1)
survived_bagging_lr.fit(X_quadratic_train, y_data)