二叉堆、优先队列与Top-N问题

前言

今日份的内容很简单，看官可以放心食用。

二叉堆

这一部分完全是大学数据结构课程的复习。

性质

顾名思义，二叉堆（binary heap）就是以二叉树形式存在的堆数据结构，也是最简单的堆。它是由J. Williams在1964年与堆排序算法一同提出的。二叉堆具有以下两个基本性质：

• 是一棵完全二叉树；
• 每个节点存储的值要么都小于等于它们的子节点的值，要么都大于等于它们的子节点的值。这两种分别称为最小堆（min-heap）和最大堆（max-heap）。

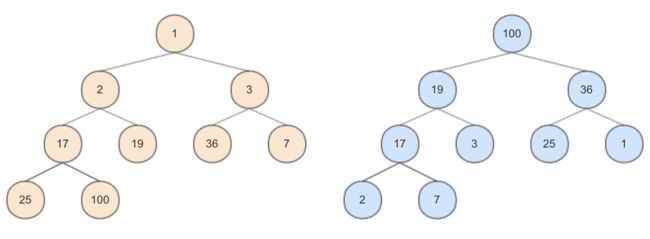
下面的图分别示出由同一个整数序列构造出的最小堆和最大堆。

基本操作

二叉堆有两种基本操作：插入（insert/sift-up）和弹出堆顶元素（extract/sift-down），在操作的过程中，需要时刻对堆进行调整，以使它总满足堆的性质。

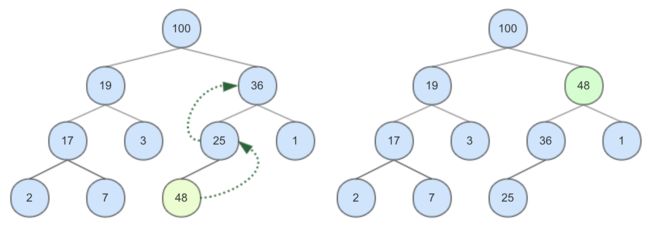
先来看插入操作，假设我们要在上图所示的最大堆中插入元素48：

将48插入堆下层最左侧的空闲位置，由于48比父节点25大，不满足堆性质，故要将48和25的位置交换。交换后，48仍然比父节点36大，需要再次交换。两次交换之后，结果满足堆性质，插入结束。可见，新节点在插入过程中是逐渐上浮的，所以也被称作sift-up。

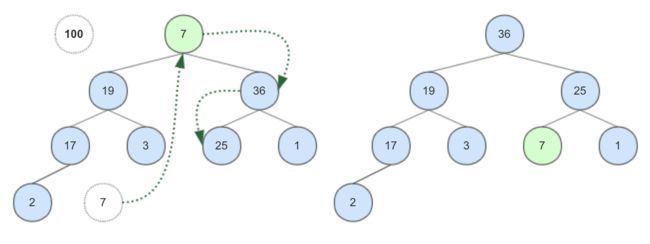
然后来看弹出堆顶元素操作。取出堆顶元素（即堆内的最大值或最小值）后，要将堆下层最右侧的元素补到堆顶。

如图所示，7在堆顶不满足最大堆的性质，它的子节点中36较大，故要将7和36的位置交换。交换后，子节点25仍然比7大，需要再次交换，此时结果又满足了堆性质。可见，弹出堆顶元素后对堆的调整操作实际上是节点逐渐下降的过程，所以也被称作sift-down。

显然，在极端情况下，一个节点会被sift-up到树的最高层，或者被sift-down到树的最底层，故插入和弹出操作的最坏时间复杂度都是O(logN)。

存储

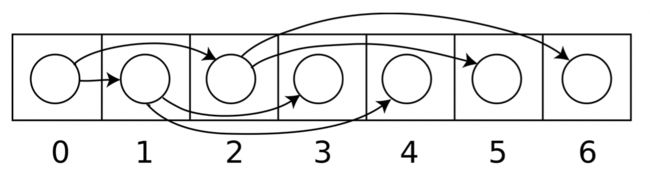
我们已经知道，完全二叉树可以很方便地用数组存储，所以二叉堆也一样。下图示出一棵有7个节点的完全（满）二叉树的数组存储。

也就是说，如果下标从0开始的话，那么对于二叉堆内下标为i的任意节点，有：

• 它的子节点下标分别为(2i + 1)和(2i + 2)；
• 它的父节点下标为floor[(i - 1) / 2]。

由于数组占用的是连续的物理内存，当堆的大小非常大并且系统启用虚拟内存时，就会被分散到许多内存页上存储，效率降低。B堆（B-heap）可以解决这个问题，详情参考这里。

二叉堆的最主要应用就是实现优先队列，下面来看。

优先队列

顾名思义，优先队列（priority queue）也是一种队列，一端进一端出。与普通队列的先进先出（FIFO）不同的是，优先队列中的每个元素都有一个与之相关的优先级，当执行出队操作时，弹出的是优先级最高的那个元素。一般来讲，优先级就是元素结构中的某个键值，如果键值小的元素优先级高，那么该队列就是升序优先队列；如果键值大的元素优先级高，那么该队列就是降序优先队列。从这个性质可以看出，二叉堆特别用来适合实现优先队列：升序对应最小堆，降序对应最大堆。

多种编程语言都内置了优先队列的实现，Java集合框架中的实现就是java.util.PriorityQueue，它另外还有一个适应并发环境的线程安全的实现：java.util.concurrent.PriorityBlockingQueue。类图如下所示。

下面来简要分析一下PriorityQueue类的源码。

成员变量

private static final int DEFAULT_INITIAL_CAPACITY = 11;
private transient Object[] queue;
private int size = 0;
private final Comparator comparator;
private transient int modCount = 0;

• DEFAULT_INITIAL_CAPACITY：队列的默认初始容量11；
• queue：存储队列（堆）元素的数组；
• size：队列的大小；
• comparator：队列元素键值的比较器。默认的二叉堆是最小堆；
• modCount：队列发生结构化修改的次数。关于它的用途，见一周前写的这篇文章。

构造方法

PriorityQueue有多种构造方法，如下图所示（其中的int为初始容量）。

所有从集合产生优先队列的构造方法最终都会调用以下的方法。

  private void initElementsFromCollection(Collection c) {
    Object[] a = c.toArray();
    // If c.toArray incorrectly doesn't return Object[], copy it.
    if (a.getClass() != Object[].class)
      a = Arrays.copyOf(a, a.length, Object[].class);
    int len = a.length;
    if (len == 1 || this.comparator != null)
      for (int i = 0; i < len; i++)
        if (a[i] == null)
          throw new NullPointerException();
    this.queue = a;
    this.size = a.length;
  }

  private void initFromCollection(Collection c) {
    initElementsFromCollection(c);
    heapify();
  }

  private void heapify() {
    for (int i = (size >>> 1) - 1; i >= 0; i--)
      siftDown(i, (E) queue[i]);
  }

heapify()方法的含义就是“堆化”，亦即将传入的集合整理成堆。siftDown()方法的源码在后面有。

入队操作

入队操作有add()和offer()两个方法实现，前者只是简单地代理了后者。

  public boolean add(E e) {
    return offer(e);
  }

  public boolean offer(E e) {
    if (e == null)
      throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
      grow(i + 1);
    size = i + 1;
    if (i == 0)
      queue[0] = e;
    else
      siftUp(i, e);
    return true;
  }

offer()方法首先对入队元素判空并增加modCount。然后，如果队列大小已经到了queue数组的长度，调用grow()方法对数组扩容。最后调用siftUp()方法插入元素到堆中，并维护堆性质。根据有无传入比较器，siftUp()方法有两种实现，下面来看默认比较逻辑下的实现方法。

  private void siftUp(int k, E x) {
    if (comparator != null)
      siftUpUsingComparator(k, x);
    else
      siftUpComparable(k, x);
  }

  private void siftUpComparable(int k, E x) {
    Comparable key = (Comparable) x;
    while (k > 0) {
      int parent = (k - 1) >>> 1;
      Object e = queue[parent];
      if (key.compareTo((E) e) >= 0)
        break;
      queue[k] = e;
      k = parent;
    }
    queue[k] = key;
  }

siftUpComparable()方法会找到父节点的下标，并调用compareTo()方法比较节点值的自然大小。由于默认是最小堆，当要插入的节点值比父节点小时，就迭代地交换它们的值，直到上浮到合适的位置。

出队操作

出队操作由poll()方法来实现。

  public E poll() {
    if (size == 0)
      return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
      siftDown(0, x);
    return result;
  }

可见确实是将队列中的最后一个元素（即二叉堆中最右下角的元素）放到最前，并调用siftDown()方法进行下沉。与siftUp()方法相似地，它也有两种逻辑，仍然来看默认的比较逻辑。

  private void siftDown(int k, E x) {
    if (comparator != null)
      siftDownUsingComparator(k, x);
    else
      siftDownComparable(k, x);
  }

  @SuppressWarnings("unchecked")
  private void siftDownComparable(int k, E x) {
    Comparable key = (Comparable) x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
      int child = (k << 1) + 1; // assume left child is least
      Object c = queue[child];
      int right = child + 1;
      if (right < size &&
        ((Comparable) c).compareTo((E) queue[right]) > 0)
        c = queue[child = right];
      if (key.compareTo((E) c) <= 0)
        break;
      queue[k] = c;
      k = child;
    }
    queue[k] = key;
  }

完全二叉树还有一个性质：如果树一共有N个节点，那么叶子节点正好有floor[N / 2]个。siftDown()方法就用这个性质来保证在当前节点不是叶子节点的情况下来循环处理。由于要保持最小堆，每次循环都会取得左、右子节点中较小的那个值，如果子节点的值小于父节点的，则交换它们。

删除操作

注意，这里的删除指的是根据下标删除优先队列中的任意一个节点。

  public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == -1)
      return false;
    else {
      removeAt(i);
      return true;
    }
  }

  private E removeAt(int i) {
    // assert i >= 0 && i < size;
    modCount++;
    int s = --size;
    if (s == i) // removed last element
      queue[i] = null;
    else {
      E moved = (E) queue[s];
      queue[s] = null;
      siftDown(i, moved);
      if (queue[i] == moved) {
        siftUp(i, moved);
        if (queue[i] != moved)
          return moved;
      }
    }
    return null;
  }

由于是从中间删除的，所以在常规的sift-down操作之后，如果发现补位元素的下标并未发生变化，说明（在默认情况下）它的左右子节点都比它大，所以还需要新一轮的sift-up操作。时间已经很晚了，所以这里就不画图了，看官稍微想一想就能理解。

查看队头元素操作

简单粗暴。

  public E peek() {
    return (size == 0) ? null : (E) queue[0];
  }

扩容操作

最后来看看前面提到过的grow()方法，不复杂。

  private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    // Double size if small; else grow by 50%
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
      (oldCapacity + 2) :
      (oldCapacity >> 1));
    // overflow-conscious code
    if (newCapacity - MAX_ARRAY_SIZE > 0)
      newCapacity = hugeCapacity(minCapacity);
    queue = Arrays.copyOf(queue, newCapacity);
  }

可见，如果当前队列长度小于64，则扩容一倍，反之则扩容一半。接下来调用hugeCapacity()方法做溢出检查，并用Arrays.copyOf()方法复制数组内容，这与ArrayList的扩容是相同的了。

用优先队列解决Top-N问题

优先队列是一种强有力的辅助工具，它可以单独用，也可以配合哈夫曼生成树、Prim算法、Dijkstra算法等以提高效率，看官如果打过算法类竞赛的话应该深有体会。而在互联网世界中，升序优先队列（最小堆）经常用来解决Top-N问题，即“取得所有帖子中阅读量排名前N的帖子”、“取得所有商品中销量排名前N的商品”等。

举个栗子，假设与商品销量相关的POJO如下：

@Getter
@Setter
public class MerchandiseSales {
  private long id;
  private long quantity;
  private long price;
  // ...
}

那么我们就可以通过如下的方法很容易地得出销量Top-N排行榜。

int topN = /*...*/;
PriorityQueue minHeap = new PriorityQueue(
  topN + 1,
  Comparator.comparingLong(MerchandiseSales::getQuantity)
);

List sales = /*...*/;
for (MerchandiseSales m : sales) {
  if (minHeap.size() < topN) {
    minHeap.offer(m);
  } else if (minHeap.peek().getQuantity() >= m.getQuantity()) {
    minHeap.poll();
    minHeap.offer(m);
  }
}

List ranking = new ArrayList<>();
for (int k = 0; k < topN && !minHeap.isEmpty(); k++) {
  ranking.add(minHeap.poll().getId());
}

需要注意的是，ranking列表中保存的商品仍然是按销量升序排列的，也就是说在实际展示排行榜时，应该从尾到头取出结果。

The End

甚累，希望12点半能睡吧。

晚安~