数据结构和算法基础
什么是数据结构和算法:兵法,计算的方法。
算法是独立存在的一种解决问题的方法和思想。
算法的特征:
- 输入:算法具有0个或多个输入
- 输出:算法至少有1个或多个输出
- 有穷性:算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成
- 确定性:算法中的每一步都有确定的含义,不会出现二义性
- 可行性:算法的每一步都是可行的,也就是说每一步都能执行有限的次数完成
时间复杂度和大O表示法
算法的优劣: 实现算法程序的执行时间可以反应出算法的效率
时间复杂度:步骤的执行速度(基本执行数量总和) + 程序运行环境(包括硬件和操作系统)
假设存在函数g,使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n)),则称O(g(n))为算法A的渐近时间复杂度,简称时间复杂度,记为T(n)T: time
三个1000次for循环: T = 1000 * 1000 * 1000 * 2 -> T(n) = n ^ 3 * 2 -> g(n) = n ^ 3, T(n) = k * g(n) -> T(n) = O(g(n))
“大O记法”:对于单调的整数函数f,如果存在一个整数函数g和实常数c>0,使得对于充分大的n总有f(n) <= c*g(n),就说函数g是f的一个渐近函数(忽略常数),记为f(n)=O(g(n))。
也就是说,在趋向无穷的极限意义下,函数f的增长速度受到函数g的约束,亦即函数f与函数g的特征相似。
最坏时间复杂度
- 算法完成工作最少需要多少基本操作,即最优时间复杂度
- 算法完成工作最多需要多少基本操作,即最坏时间复杂度
- 算法完成工作平均需要多少基本操作,即平均时间复杂度
最优时间复杂度,其价值不大。
最坏时间复杂度,提供了一种保证,(只要关注,最坏时间复杂度)
平均时间复杂度,是对算法的一个全面评价。
时间复杂度的几条基本计算规则
- 基本步骤,即只有常数项,认为其时间复杂度为O(1)
- 顺序结构,时间复杂度按加法进行计算
- 循环结构,时间复杂度按乘法进行计算
- 分支结构,时间复杂度取最大值(
if或者else哪个步数最多) - 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
- 在没有特殊说明时,所分析的算法的时间复杂度都是指最坏时间复杂度
计算方式:
# for a in range(0, n):
# for b in range(0, n):
# c = 1000 - a - b
# if a ** 2 + b ** 2 == c **2:
# print('a, b, c为:%d'%(a, b, c))
# T(1000) = 1000 * 1000 * (1 + 1)
# T(n) = n * n * (1 + max(1, 0))
# = n ^ 2 * 2
# = O(n ^ 2)常见时间复杂度与大小关系
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n^2+2n+1 | O(n^2) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
Note: 经常将log2n(以2为底的对数)简写成logn
所消耗的时间从小到大:O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(n^n)
Note:函数是步骤和执行结构的综合
Python内置类型性能
timeit模块作用:测试一小段Python代码代码的执行速度
class timeit.Timer(stmt='pass', setup='pass', timer=Timer是测量小段代码执行速度的类。stmt参数是要测试的代码语句(statment);setup参数是运行代码时需要的设置;timer参数是一个定时器函数,与平台有关。
#coding=utf-8
from timeit import Timer
def test1():
li = []
for i in range(10000):
li.append(i)
def test2():
li = []
for i in range(10000):
li += [i]
def test3():
li = [i for i in range(10000)]
def test4():
li = list(range(10000))
timer1 = Timer('test1()', 'from __main__ import test1')
print('append: ',timer1.timeit(1000)) # 测算次数, 返回值测算时间
timer2 = Timer('test2()', 'from __main__ import test2')
print('+: ',timer1.timeit(1000))
timer3 = Timer('test3()', 'from __main__ import test3')
print('[]: ',timer1.timeit(1000))
timer4 = Timer('test4()', 'from __main__ import test4')
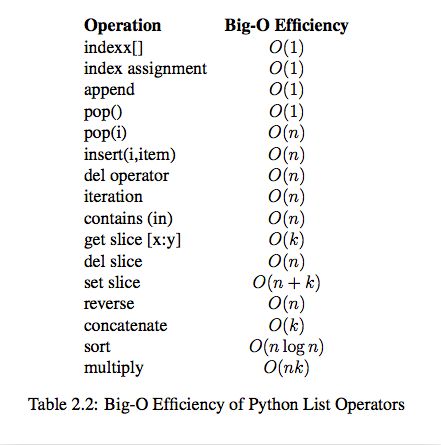
print('list: ',timer1.timeit(1000))list内置操作的时间复杂度:
n: 列表长度k: 范围
主要:
index[] -> O(1)
append -> O(1)
pop(i) -> O(n)
insert(i, item) -> O(n)
contains(in) -> O(n)dict内置操作的时间复杂度:
数据结构引入
算法关注在解决问题的步骤和思想上面。
什么是数据结构:数据的组织结构方式,(一组数据如何存储),基本数据类型(int, float,char)的封装
算法与数据结构的区别:
数据结构只是静态的描述了数据元素之间的关系。
高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法
总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
最常用的数据运算有五种:
- 插入
- 删除
- 修改
- 查找
- 排序
顺序表
内存
32位机器:一个int, 占四个字节。
变量表示起始地址位置
内存的基本信息:
- 单位:字节,
1byte == 8bit - 连续的存储空间
- 一个字节表示一个地址单元
类型本质
任何变量,函数原则上都是一块块大小各异的内存,而类型则是和系统对这块内存含义的约定(固定内存块大小的别名)
决定在内存中占多少个单元
基本顺序表与元素外围顺序表
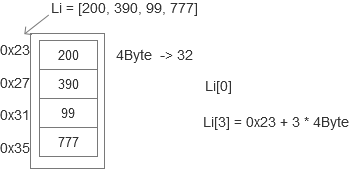
顺序表的基本布局:
数据元素本身连续存储,每个元素所占的存储单元大小固定相同,元素的下标是其逻辑地址,而元素存储的物理地址(实际内存地址)可以通过存储区的起始地址Loc (e0)加上逻辑地址(第i个元素)与存储单元大小(c)的乘积计算而得
所以,访问指定元素时无需从头遍历,通过计算便可获得对应地址,其时间复杂度为O(1)
下标:地址单元的偏移量,才会规定为从0开始。
顺序表的元素外置基本布局:
元素外置在内存中存储地址,地址字节是相同的(可以使用顺序表),而非变化的字节。
顺序表的一体式结构与分离式结构
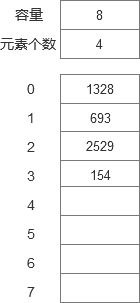
顺序表 = 数据区(元素集合) + 表头信息(容量 + 元素个数)
容量: 在最初始的时候,就要预估当前规模,一次性向操作系统申请内存地址 (最大存储多少)
元素个数:当前存储多少
顺序表的基本实现方式(表头和数据区如何组合在一起):
- 一体式结构:
优点: 一次性申请, 整体性强,易于管理。
缺点:元素存储区就固定。当数据存储不下的时候,需要整体替换重新向操作系统申请 - 分离式结构:
优点:元素存储区不固定。
缺点:分二次申请,不易管理
最大区别:分离式其实位置(表头)的地址不变,而一体式,需要整体替换(表头和数据区)都需要重新申请。
顺序表数据区替换与扩充
重新扩充的两种策略:
- 每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。
特点:节省空间,但是扩充操作频繁,操作次数多。 - 每次扩充容量加倍,如每次扩充增加一倍存储空间。
特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式。
顺序表的操作
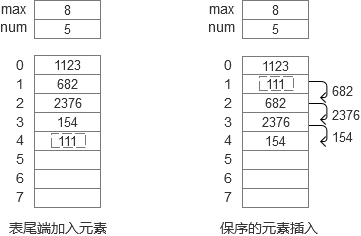
添加元素:
尾端加入元素,时间复杂度为O(1)
保序的元素加入,时间复杂度为O(n)
删除元素:
删除表尾元素,时间复杂度为O(1)
保序的元素删除,时间复杂度为O(n)
Python中的list和tuple两种类型采用了顺序表的实现技术.list就是一种采用分离式技术实现的动态顺序表
list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。
单链表
为什么需要链表
顺序表缺点:
- 需要预先知道数据大小来申请存储空间
- 进行扩充时需要进行数据的搬迁
- 灵活性低
手拉手的方式(线串)去存储,而非通过元素外置的方式去存储,元素外置需要预先知道数据大小。
线性表:
一维空间的一条线去组织数据,呈线性状态。
- 顺序表:将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示。
- 链表:将元素存放在通过链接构造起来的一系列存储块中。
原本的数据区,不单单仅仅存储数据,而会增加一个下一个的单元地址
单链表的ADT模型
头节点:开始存储的变量
尾节点:往后就是空指针
变量p指向链表的头节点(首节点)的位置,从p出发能找到表中的任意节点。
单链表的操作:
is_empty() 链表是否为空
length() 链表长度
travel() 遍历整个链表
add(item) 链表头部添加元素
append(item) 链表尾部添加元素
insert(pos, item) 指定位置添加元素
remove(item) 删除节点
search(item) 查找节点是否存在Python中变量标识的本质: 存储地址,引用指向到一个实际数据
单链表的实现
# coding=utf-8
# single_link_list
class Node(object):
'''节点'''
def __init__(self, elem):
self.elem = elem
self.next = None
# node = Node(100) # 保存 elem, next
class SingleLinkList(object):
'''单链表'''
def __init__(self, node=None):
self.__head = node # 头节点
def is_empty(self):
'''链表是否为空'''
return self.__head == None
def length(self):
'''链表长度'''
# 游标, 指针
# cur游标,用来移动遍历节点
cur = self.__head
# count记录数量
count = 0
while cur != None: # cur.next == None
count += 1
cur = cur.next
return count
def travel(self):
'''遍历整个链表'''
cur = self.__head
while cur != None:
print(cur.elem, end=' ')
cur = cur.next
def add(self, item):
'''链表头部添加元素,头插法'''
node = Node(item)
node.next = self.__head # 保证链表中的所有关系不打断
self.__head = node
def append(self, item):
'''链表尾部添加元素,尾插法'''
# item 数据元素
node = Node(item)
if self.is_empty():
self.__head = node
else:
cur = self.__head
while cur.next != None: # 从头往后走,然后最后挂载一个新的游标
cur = cur.next
cur.next = node
def insert(self, pos, item):
'''指定位置添加元素
:param pos 从0开始
'''
if pos < 0:
self.add(item)
elif pos > self.length() - 1:
self.append(item)
else:
# pre用来指向指定位置pos的前一个位置pos-1,初始从头节点开始移动到指定位置
pre = self.__head # pre, prior
count = 0
while count < pos - 1:
count += 1
pre = pre.next
# 当循环退出后,pre指向pos-1的位置
node = Node(item)
# 先将新节点node的next指向插入位置的节点
node.next = pre.next
# 将插入位置的前一个节点的next指向新节点
pre.next = node
def remove(self, item):
'''删除节点'''
# pre 与 cur 二个游标,需要隔开移动
cur = self.__head
pre = None
while cur != None:
if cur.elem == item:
# 如果第一个就是删除的节点
if cur == self.__head:
# 判断子节点是否是头节点
self.__head = cur.next # 将头指针指向头节点的后一个节点
else:
# 将删除位置前一个节点的next指向删除位置的后一个节点
pre.next = cur.next
break
else:
# 继续按链表后移节点
pre = cur
cur = cur.next
def search(self, item):
'''查找节点是否存在'''
cur = self.__head
while cur != None:
if cur.elem == item:
return True
else:
cur = cur.next
return False
if __name__ == '__main__':
sll = SingleLinkList()
print('is_empty', sll.is_empty())
print('length', sll.length())
sll.append(100)
print('is_empty', sll.is_empty())
print('length', sll.length())
sll.append(22)
sll.add(7)
sll.append(20)
sll.insert(2, 777)
sll.travel()
sll.remove(7)
sll.travel()
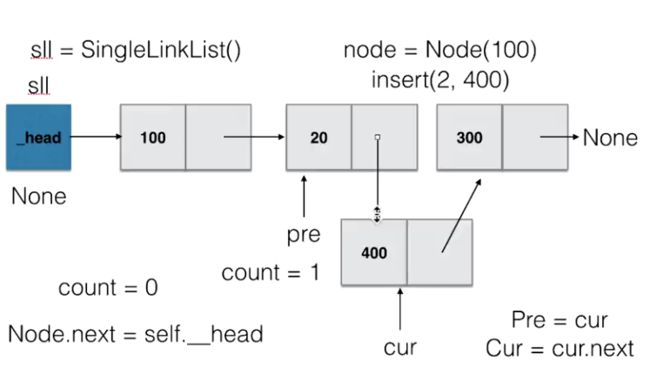
insert示意图:
remove示意图:
后继结点:当前节点的下一个节点
单链表与顺序表的对比
链表失去了顺序表随机读取的优点,同时链表由于增加了节点的指针域,空间开销比较大,但对存储空间的使用要相对灵活。
链表与顺序表的各种操作复杂度:
| 操作 | 链表 | 顺序表 |
|---|---|---|
| 访问元素 | O(n) | O(1) |
| 在头部插入/删除 | O(1) | O(n) |
| 在尾部插入/删除 | O(n) | O(1) |
| 在中间插入/删除 | O(n) | O(n) |
链表不能一次性找到位置,都需要通过循环来找到该位置;而顺序表则直接找到位置。
双链表
数据包含:数据区 + 前驱结点 + 后继结点
# coding=utf-8
# double_link_list
class Node(object):
'''节点'''
def __init__(self, elem):
self.elem = elem
self.next = None
self.prev = None
class DoubleLinkList(object):
"""双链表"""
def __init__(self, node=None):
self.__head = node
def is_empty(self):
return self.__head is None
def length(self):
count = 0
cur = self.__head
while cur != None:
count += 1
cur = cur.next
return count
def travel(self):
cur = self.__head
while cur != None:
print(cur.elem, end=' ')
cur = cur.next
print('')
def add(self, item):
node = Node(item)
node.next = self.__head
self.__head = node
node.next.prev = node
def append(self, item):
node = Node(item)
cur = self.__head
if self.is_empty():
self.__head = node
else:
while cur.next != None:
cur = cur.next
cur.next = node
node.prev = cur
def insert(self, pos, item):
if pos <= 0:
self.add(item)
elif pos > (self.length() - 1):
self.append(item)
else:
cur = self.__head
count = 0
while count < pos:
count += 1
cur = cur.next
# 当循环退出的时候,cur指针指向的就是pos的位置
node = Node(item)
# 将node的prev指向cur
node.next = cur
# 将node的next指向cur的下一个节点
node.prev = cur.prev # 当前节点的上一个,指向到插入节点的前指针
# 将cur的下一个节点的prev指向node
cur.prev.next = node
# 将cur的next指向node
cur.prev = node
def remove(self, item):
cur = self.__head
while cur != None:
if cur.elem == item:
if cur == self.__head:
self.__head = cur.next
if cur.next: # 判断双链表是否之后一个节点
cur.next.prve = None
else:
# 将cur的前一个节点的next指向cur的后一个节点
cur.prev.next = cur.next
if cur.next:
# 将cur的后一个节点的prev指向cur的前一个节点
cur.next.prev = cur.prev
break
else:
cur = cur.next
def search(self, item):
cur = self.__head
while cur != None:
if cur.elem == item:
return True
else:
cur = cur.next
return False
if __name__ == '__main__':
dll = DoubleLinkList()
print('is_empty', dll.is_empty())
print('length', dll.length())
dll.append(100)
print('is_empty', dll.is_empty())
print('length', dll.length())
dll.append(22)
dll.add(7)
dll.append(20)
dll.insert(2, 777)
dll.travel()
dll.remove(7)
dll.travel()单项循环链表
# coding=utf-8
# single_cycle_link_list
class Node(object):
'''节点'''
def __init__(self, node):
self.elem = node
self.next = None
class SingleCycleLinkList(object):
'''单链表'''
def __init__(self, node=None):
self.__head = node # 头节点
if node:
node.next = node
def is_empty(self):
'''链表是否为空'''
return self.__head == None
def length(self):
'''链表长度'''
if self.is_empty():
return 0
cur = self.__head
# count记录数量
count = 1 # count从1开始
while cur.next != self.__head: # cur.next == None
count += 1
cur = cur.next
return count
def travel(self):
'''遍历整个链表'''
if self.is_empty():
return
cur = self.__head
while cur.next != self.__head:
cur = cur.next
print(cur.elem, end=' ')
# print(cur.elem, '-------')
# print('')
def add(self, item):
'''链表头部添加元素,头插法'''
node = Node(item)
if self.is_empty():
# 如果为空,指向节点,然后节点的指针指向自己
self.__head = node
node.next = node
else:
cur = self.__head
# 指针先移动到尾端
while cur.next != self.__head:
cur = cur.next
# 退出循环,cur指向尾节点
# 改变指针指向
node.next = self.__head
self.__head = node
# cur.next = node
cur.next = node
def append(self, item):
'''链表尾部添加元素,尾插法'''
node = Node(item)
if self.is_empty():
self.__head = node
node.next = node
else:
cur = self.__head
while cur.next != self.__head:
cur = cur.next
node.next = self.__head
cur.next = node
def insert(self, pos, item):
'''指定位置添加元素
:param pos 从0开始
'''
if pos < 0:
self.add(item)
elif pos > (self.length() - 1):
self.append(item)
else:
pre = self.__head
count = 0
while count < (pos - 1):
count += 1
pre = pre.next
node = Node(item)
node.next = pre.next
pre.next = node
def remove(self, item):
'''删除节点'''
'''
1. 头节点
2. 尾节点
3. 中间节点
4. 只存在一个节点
5. 空链表
6. 首节点就是删除的节点
'''
if self.is_empty():
return
cur = self.__head
pre = None
while cur.next != self.__head:
if cur.elem == item:
if cur == self.__head:
# 头节点的情况
# 找到尾节点
rear = self.__head
# 为了顺利把尾节点的指针指向到头节点,先把指针便利到尾部
while rear.next != self.__head:
rear = rear.next
self.__head = cur.next
rear.next = self.__head
else:
# 中间节点
pre.next = cur.next
return
else:
# 两个游标顺次往链表后边移动
pre = cur
cur = cur.next
# 尾部情况
# 退出循环,cur指向尾节点
if cur.elem == item:
if self.__head == cur:
# 只有一个节点
self.__head = None
else:
pre.next = cur.next
def search(self, item):
'''查找节点是否存在'''
if self.is_empty():
return False
cur = self.__head
while cur.next != self.__head:
if cur.elem == item:
return True
else:
cur = cur.next
# 退出循环,cur指向尾节点
if cur.elem == item:
return True
return False
if __name__ == '__main__':
scll = SingleCycleLinkList()
print('is_empty', scll.is_empty())
print('length', scll.length())
scll.append(100)
print('is_empty', scll.is_empty())
print('length', scll.length())
scll.append(22)
scll.add(7)
scll.append(20)
scll.insert(2, 777)
scll.travel()
scll.remove(7)
scll.travel()
栈
线性表:顺序表(连续存放),链表(离散存放)。存储线性的数据。 --> 解决数据怎么存放的问题
栈与队列基础
栈:容器,可以利用线性表的特性,来实现数据的操作。
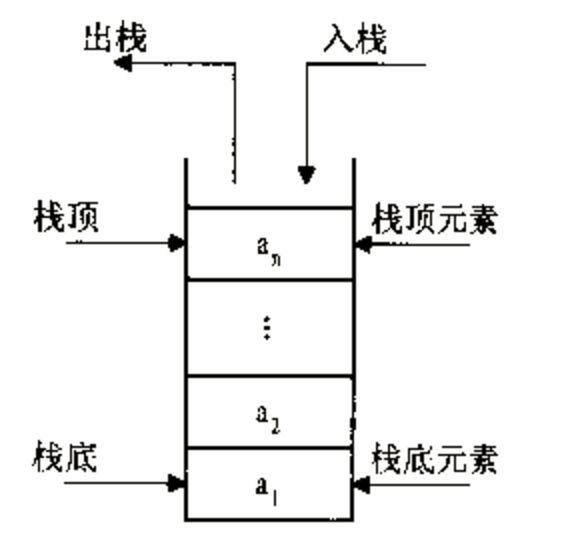
由于栈数据结构只允许在一端进行操作,因而按照后进先出(LIFO, Last In First Out)的原理运作。
栈的实现
在python的list是顺序表,借助list来实现栈.
栈顶:栈的头部
栈低:栈的底部
#coding=utf-8
class Stack(object):
'''栈'''
def __init__(self):
self.__list = []
def push(self, item):
'''添加一个新的元素item到栈顶'''
self.__list.append(item)
# 确定是尾部还是头部插入数据
# 选择在尾部添加,而非头部插入,顺序表对于尾部操作的时间复杂度是O(1)
# self.__list.insert(0, item)
def pop(self):
'''弹出栈顶元素'''
return self.__list.pop()
# self.__list.pop(0)
def size(self):
'''返回栈的元素个数'''
return len(self.__list)
def is_empty(self):
'''判断栈是否为空'''
# '', 0, {}, [], ()
return self.__list == []
def peek(self):
'''返回栈顶元素'''
if self.__list:
return self.__list[-1]
else:
return None
if __name__ == '__main__':
stack = Stack()
stack.push(11)
stack.push(1000)
print(stack.size(), 'stack.size()')
print(stack.pop(), 'stack.pop()')
队列
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列不允许在中间部位进行操作。
可以在tree中使用.
队列
队列头:取的那一端,叫做队头
队列尾:添加队一端,叫做队尾
队列
#coding=utf-8
class Queue(object):
def __init__(self):
self.__list = []
def enqueue(self, item):
'''往队列中添加一个item元素'''
self.__list.append(item) # 尾部插入
# self.__list.insert(0, item) # 头部插入
def dequeue(self):
'''从队列头部删除一个元素'''
return self.__list.pop(0) # 尾部删除
# return self.__list.pop() # 头部删除
def is_empty(self):
'''判断一个队列是否为空'''
return not self.__list
def size(self):
'''返回队列的大小'''
return len(self.__list)
if __name__ == '__main__':
queue = Queue()
queue.enqueue(10)
queue.enqueue(13)
print(queue.size())
print(queue.dequeue())
双端队列
两端都可以出队列,也都可以入队列。
#coding=utf-8
class Dqueue(object):
'''双端队列'''
def __init__(self):
self.__list = []
def add_front(self, item):
'''添加一个新的元素item到栈顶'''
self.__list.insert(0, item) # 头部添加
def add_rear(self, item):
self.__list.append(item) # 尾部添加
def pop_fornt(self):
return self.__list.pop(0)
def pop_rear(self):
return self.__list.pop()
def size(self):
'''返回栈的元素个数'''
return len(self.__list)
def is_empty(self):
'''判断栈是否为空'''
# '', 0, {}, [], ()
return self.__list == []
if __name__ == '__main__':
dq = Dqueue()
dq.add_front(11)
dq.add_front(100)
dq.add_rear(1000)
print(dq.size(), 'dq.size()')
print(dq.pop_fornt(), 'dq.pop_fornt()')
排序
排序算法:是一种能将一串数据依照特定顺序进行排列的一种算法。
排序算法的稳定性
稳定排序算法会让原本有相等键值的记录维持相对次序。也就是如果一个排序算法是稳定的,当有两个相等键值的纪录R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。(特指排序条件相等的两个元素,排序后的顺序是否和排序前一致。有时候需要按照多个条件排序)
如果排序算法是稳定的,可以先按照第一个条件排序后再按照其它条件排序,则结果就是想要的。若果是不稳定的排序,需要额外的步骤保证结果的正确性。
冒泡排序
- 比较相邻的元素。如果第一个比第二个大(升序),就交换它们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#condig-utf8
def bubble_sort(alist):
'''冒泡排序'''
n = len(alist)
# 走多少次
# 从头走到尾
for j in range(n - 1):# 走多少次
count = 0
for i in range(0, n - 1 - j): # 从头走到尾
if alist[i] > alist[i+1]:
# 位置调换
alist[i], alist[i+1] = alist[i+1], alist[i]
count += 1
if 0 == count: # 常量 ,变量
return
# i 0 ~ n-2 range(0, n-1) j=0
# i 1 ~ n-3 range(0, n-1-1) j=1
# i 2 ~ n-4 range(0, n-1-1-1) j=2
# j=n i range(0, n-1-j)
if __name__ == '__main__':
li = [54, 26, 93, 17, 77, 34]
bubble_sort(li)
print(li)
时间复杂度:
- 最优时间复杂度:
O(n)(表示遍历一次发现没有任何可以交换的元素,排序结束。) - 最坏时间复杂度:
O(n^2) - 稳定性:稳定
选择排序
从未排序的列表中选择一个最小的排到前面去
# alist = [12, 34, 3453, 456, 4, 45, 2, 5, 100]
# 0 1 2 3 4 5 6 7 8
# min = 0
# min = 6
# alist[0], alist[6] = alist[6], alist[0]
# alist = [2, 34, 3453, 456, 4, 45, 12, 5, 100]
# 0 1 2 3 4 5 6 7 8
# min = 1
# min = 4
# alist[1], alist[4] = alist[4], alist[1]
# 从未排序的列表中选择一个最小的排到前面去
# 选择排序,看未排序的后边部分
# 插入排序,把未排序的序列放在,已经排序的序列那一个位置中。
# 比较的位置
# j = 0
# min = 0 + 1
# j = 1
# min = 1 + 1
alist = [12, 34, 3453, 456, 4, 45, 2, 5, 100]
def select_sort(alist):
'''选择排序'''
n = len(alist)
for j in range(0, n-1): # 产生n-2, 这边需要写n-1, 及 (0 ~ n-2)
min_index = j
for i in range(j+1, n): # 需要到 (n-1) 的位置 时间复杂度:1-n, 2-n, 3-n
# 分为左右两边,完成的序列 和 未完成的序列
if alist[min_index] > alist[i]:
min_index = i
alist[j], alist[min_index] = alist[min_index], alist[j]
print(alist)
select_sort(alist)
print(alist)
时间复杂度:
- 最优时间复杂度:
O(n^2) - 最坏时间复杂度:
O(n^2) - 稳定性:不稳定(考虑升序每次选择最大的情况)
相同数据中,排列之后的位置一样,具有稳定性。
插入排序
#coding=utf-8
li = [54, 26, 93, 17, 77, 34]
# 后续的无需序列,与前面的有序序列中的最后一个元素比较
def insert_sort(alist):
n = len(alist)
# 从右边的无序序列中取出多少个元素执行这个的过程
for j in range(0, n):
i = j
# 执行从右边的无序序列中取出第一个元素,即i位置的元素,然后将其插入到前面正确的位置中
while i > 0:
if alist[i] < alist[i-1]:
alist[i], alist[i-1] = alist[i-1], alist[i]
i -= 1
else:
break
print(li)
insert_sort(li)
print(li)
时间复杂度:
- 最优时间复杂度:
O(n)(升序排列,序列已经处于升序状态) - 最坏时间复杂度:
O(n^2) - 稳定性:稳定
希尔排序
插入排序的改进版本
#coding=utf-8
alist = [12, 34, 3453, 456, 4, 45, 2, 5, 100]
def shell_sort(alist):
'''希尔排序'''
n = len(alist) # n = 9
gap = n // 2 # n = 4
# i = 1
# i = gap
# gap变化到0之前,插入算法执行到次数
while gap > 0: # 可以等于0
# 希尔算法 与普通的 插入算法的区别就是 gap 步长
for j in range(gap, n): # 一次性循环全部处理完成
# 控制子序列中的所有元素
# j = [gap, gap+1, gap+2, gap+3, ... , n-1]
i = j
while i > 0: # 控制子序列中的比较和交换的算法
if alist[i] < alist[i-gap]:
alist[i], alist[i-gap] = alist[i-gap], alist[i]
i -= gap
else:
break
gap //= 2 # 缩短gap步长
print(alist)
shell_sort(alist)
print(alist)时间复杂度:
- 最优时间复杂度:根据步长序列的不同而不同
- 最坏时间复杂度:O(n^2)
- 稳定性:不稳定
快速排序
一个数字,在序列的那个位置。按照当前的数字,每次分开两部分。
步骤:
- 从数列中挑出一个元素,称为"基准"(
pivot), - 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(
partition)操作。 - 递归地(
recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
核心代码:
取第一个位置保存中间值(middle_value), 第一个位置是空位置,就该high的位置来判断了,当合适就换位置,并且移动对方的指针(low),当不合适移动当前指针(high)。
middle_value = 10
low = 0
high = len(list)
if alist[high] < middle_value:
alist[low] = alist[high]
low += 1
elif alist[high] > middle_value:
high -= 1
if alist[low] < middle_value:
alist[high] = alist[low]
hight -= 1
elif alist[low] > middle_value:
low += 1
if low == high:
alist[low] = middle_value #conding=utf-8
def quick_sort(alist, first, last):
'''快速排序'''
if first >= last:
return
# mid_value = alist[0] # 中间值
mid_value = alist[first] # 中间值
# n = len(alist)
# 左右游标
# low = 0
low = first
# high = n-1
high = last
while low < high:
# high 游标 左移动
while low < high and alist[high] >= mid_value:
high -= 1
alist[low] = alist[high]
# low += 1
# low 游标 右移动
while low < high and alist[low] < mid_value:
low += 1
alist[high] = alist[low]
# high -= 1
# 等于的情况放到其中一边去处理
# 为了保证二个指针不错过,注释 【low += 1】和 【high -= 1】
# 退出循环的时候,low == high
alist[low] = mid_value # 中间值赋值到该位置
# 递归
# 对low左边的列表执行快速排序
quick_sort(alist, first, low-1)
# 对low右边的列表执行快速排序
quick_sort(alist, low+1, last)
if __name__ == '__main__':
li = [54, 26, 93, 17, 77, 34]
print(li)
quick_sort(li, 0, len(li)-1)
print(li)
时间复杂度:
- 最优时间复杂度:
O(nlogn):2*2*2... = n, n个元素对2取对数。log2(n)以2为底的对数 - 最坏时间复杂度:
O(n^2) - 稳定性:不稳定
时间复杂度不好从代码中分析,通过画图中理解每次循环中操作。横向和纵向来区分判断。
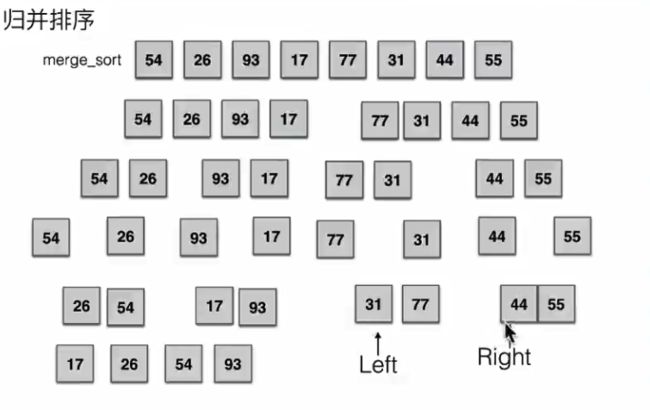
归并排序
先把序列从头开始往下拆,直到只有一个元素。紧接着开始,二个部分合并到一起,然后再次合并,直到完成序列合并。
需要使用到递归。
#coding=utf-8
def merge_sort(alist):
'''归并排序'''
'''
分裂
'''
n = len(alist)
if n <= 1:
return alist
mid = n // 2
# left, right 采用归并排序后形成的有序的新的列表
left_li = merge_sort(alist[:mid]) # 传新的列表
right_li = merge_sort(alist[mid:])
'''
合并
'''
# 将两个有序的子序列合并为一个新的整体
# merge(left, right)
left_pointer, right_pointer = 0, 0
result = []
while left_pointer < len(left_li) and right_pointer < len(right_li):
if left_li[left_pointer] < right_li[right_pointer]: # 左边
result.append(left_li[left_pointer])
left_pointer += 1
else: # 右边
result.append(right_li[right_pointer])
right_pointer += 1
result += left_li[left_pointer:] # 加上剩下数据
result += right_li[right_pointer:]
return result
alist = [1, 23, 34, 6,2, 12, 12, 1, 2]
print(alist)
new_alist = merge_sort(alist) # 返回新的列表
print(new_alist)时间复杂度:
- 最优时间复杂度:
O(nlogn),2*2*2... = n, n个元素对2取对数。log2(n)以2为底的对数 - 最坏时间复杂度:
O(nlogn) - 稳定性:稳定
搜索
搜索:在一个项目集合中找到特定项目的算法过程。
搜索结果:通常的答案是真或假,因为该项目是否存在。
常见搜索方法:顺序查找,二分法查找,二叉树查找,哈希查找
二分查找
二分查找,需要定位到索引,也就是说,只能作用到顺序表上,而且是排序过后的,有序顺序表中。
非递归实现
需要关注:头和尾的下标,来计算二分位置的下标。(原因在原有的列表上去找)
指明查找的范围,需要二个指针来控制前后移动
def binary_search_2(alist, item):
'''二分查找'''
n = len(alist)
first = 0
last = n - 1
while first <= last: # 中间最小之后一个值,需要包含等于
mid = (first + last) // 2
if alist[mid] == item:
return True
elif item < alist[mid]:
last = mid - 1
else:
first = mid + 1
return False递归实现
def binary_search(alist, item):
'''二分查找'''
n = len(alist)
if n > 0:
mid = n//2 # 新的列表
if alist[mid] == item:
return True
elif item < alist[mid]:
return binary_search(alist[:mid], item)
else:
return binary_search(alist[mid+1:], item)
return False时间复杂度:
- 最优时间复杂度:
O(1) - 最坏时间复杂度:
O(logn)
二叉树
用来模拟具有树状结构性质的数据集合,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
二叉树是二维空间上的表现,图是三维空间上的表现。
特点:
- 每个节点有零个或多个子节点(每个节点都会有数据区和链接区)
- 没有父节点的节点称为根节点
- 每一个非根节点有且只有一个父节点
- 除了根节点外,每个子节点可以分为多个不相交的子树(每个节点只有一个父级)
树的术语
- 节点的度:一个节点含有的子树的个数称为该节点的度(有几个下级,几个下级子节点)
- 树的度:一棵树中,最大的节点的度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
-
有序树:树中任意节点的子节点之间有顺序关系(树的节点直接有某种特殊的意义在),这种树称为有序树;
-
二叉树:每个节点最多含有两个子树的树称为二叉树(节点的度最高到2)
- 完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树,其中满二叉树的定义是所有叶节点都在最底层的完全二叉树
- 平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树
- 排序二叉树(二叉查找树(英语:
Binary Search Tree),也称二叉搜索树、有序二叉树)
- 霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树
- B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树
-
树的存储与表示
虽然树是二维的,但是可以用一维的顺序表存储起来。
- 顺序存储:将数据结构存储在固定的数组中,然在遍历速度上有一定的优势,但因所占空间比较大,是非主流二叉树。二叉树通常以链式存储。(把连续的空间和树上的节点做对应关系。按照节点的层次来存储数据)
- 链式存储:缺陷,指针域指针个数不定
由于对节点的个数无法掌握,常见树的存储表示都转换成二叉树进行处理,子节点个数最多为2
最常用的树的存储,是链式存储,多存储后记链接区。
常见应用场景
-
xml,html等,那么编写这些东西的解析器的时候,不可避免用到树 - 路由协议就是使用了树的算法
-
mysql数据库索引 - 文件系统的目录结构
- 所以很多经典的AI算法其实都是树搜索,此外机器学习中的
decision tree也是树结构
二叉树介绍
每个节点最多有两个子树的树结构。(最大的度只能是2)
通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)
二叉树的数学上的一些性质(特性)
- 在二叉树的第
i层上至多有2^(i-1)个结点(i>0) - 深度为
k的二叉树至多有2^k - 1个结点(k>0) - 对于任意一棵二叉树,如果其叶结点数为
N0(度数为0),而度数为2的结点总数为N2,则N0=N2+1; - 具有
n个结点的完全二叉树的深度必为log2(n+1)(和特性2在数学上是相反的) - 对完全二叉树,若从上至下、从左至右编号,则编号为
i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1时为根,除外)
二叉树的实现
添加的方式:二叉树的广度优先遍历(广度层次遍历),通过队列,取出头的元素,判断是否有左子节点与右子节点,如果都有往队列中添加,如果没有,挂载到节点上。
深度遍历:
- 先序遍历(从最小的三个节点二叉树的先根节点遍历,左子节点,右子节点的遍历)-> 根,左,右
- 中序遍历(把根放到中间,就是左子节点,根,右子节点的顺序遍历)-> 左,根,右
- 后序遍历(把根放到最后一个上面,左子节点,右子节点的顺序遍历)-> 左,右,根
无论把根放到那个位置上,子节点都是先左边后右边
#coding=utf-8
class Node(object):
'''节点类'''
def __init__(self, item):
self.elem = item
self.lchild = None
self.rchild = None
class Tree(object):
'''二叉树'''
def __init__(self):
self.root = None
# 插入 (广度优先遍历)
def add (self, item):
node = Node(item)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue: # 不为空列表
cur_node = queue.pop(0)
if cur_node.lchild is None:
cur_node.lchild = node
return
else:
queue.append(cur_node.lchild)
if cur_node.rchild is None:
cur_node.rchild = node
return
else:
queue.append(cur_node.rchild)
def breadth_travel(self):
'''广度遍历'''
'''层次遍历'''
if self.root is None:
return
queue = [self.root]
while queue:
cur_node = queue.pop(0)
print(cur_node.elem, end=' ')
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
def preorder(self, node): # 中序,先序,后序,根节点都在变化,为了调用自身,而且是调用不同的子树,所以根节点作为参数传入
'''先序遍历'''
if node is None:
return
print(node.elem, end=' ') # 根
self.preorder(node.lchild) # 左边
self.preorder(node.rchild) # 右边
def inorder(self, node):
'''中序遍历'''
if node is None:
return
self.inorder(node.lchild)
print(node.elem, end=' ')
self.inorder(node.rchild)
def postorder(self, node):
'''后序遍历'''
if node is None:
return
self.postorder(node.lchild)
self.postorder(node.rchild)
print(node.elem, end=' ')
if __name__ == '__main__':
tree = Tree()
tree.add(0)
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
tree.breadth_travel()
print(' ')
tree.preorder(tree.root)
print(' ')
tree.inorder(tree.root)
print(' ')
tree.postorder(tree.root)
print(' ')
层次遍历: 0 1 2 3 4 5 6 7 8 9
先序遍历: 0 1 3 7 8 4 9 2 5 6
中序遍历: 7 3 8 1 9 4 0 5 2 6
后序遍历: 7 8 3 9 4 1 5 6 2 0给出遍历结果,然后确定一颗二叉树。给其中二个种遍历结果,就可以写出二叉树(先序和中序,或者,中序和后序),一定需要一个中序,不然,左右子树无法分开。