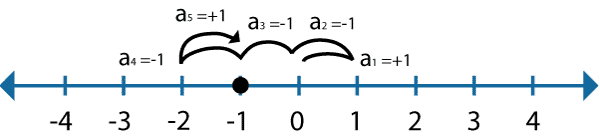- 使用 FinalShell 进行远程连接(ssh 远程连接 Linux 服务器)
编程经验分享
开发工具服务器sshlinux
目录前言基本使用教程新建远程连接连接主机自定义命令路由追踪前言后端开发,必然需要和服务器打交道,部署应用,排查问题,查看运行日志等等。一般服务器都是集中部署在机房中,也有一些直接是云服务器,总而言之,程序员不可能直接和服务器直接操作,一般都是通过ssh连接来登录服务器。刚接触远程连接时,使用的是XSHELL来远程连接服务器,连接上就能够操作远程服务器了,但是仅用XSHELL并没有上传下载文件的功能
- Some jenkins settings
SnC_
Jenkins连接到特定gitlabproject的特定branch我采用的方法是在pipeline的script中使用git命令来指定branch。如下:stage('Clonerepository'){steps{gitbranch:'develop',credentialsId:'gitlab-credential-id',url:'http://gitlab.com/repo.git'}}
- CentOS7 安装MySQL5.7.44
不要Null了
javacentosmysql
1.下载mysql安装包,我放在百度网盘里(下方链接)链接:https://pan.baidu.com/s/1_Mn1XW_1mWdTV4mhnLG66A提取码:s31n2.首先看看以前是否安装过mysqlrpm-qa|grep-imysql如果已经安装过mysql会提示卸载mysqlrpm-emysql-…3.使用FinallShell或者Xftp进行上传放到/usr/local/mysql,没
- CMU 15-445/645 Lab2-B+Tree Index
yyy_3y
CMU-15/445b树数据结构CMU15-445数据库
0.写在前面GitHub同步更新https://github.com/kaniel-outis/CMU15-445Lab2的地址:https://15445.courses.cs.cmu.edu/fall2020/project2/本文主要总结一下在写Lab2需要的基础知识以及Task的解决思路(不公开代码,如果有问题可以留言)。Lab2的主要内容是B+tree的定义和Insert、Delete操
- HALTT4LLM:大型语言模型的幻觉检测指标
谢忻含Norma
HALTT4LLM:大型语言模型的幻觉检测指标haltt4llmThisprojectisanattempttocreateacommonmetrictotestLLM'sforprogressineliminatinghallucinationswhichisthemostseriouscurrentprobleminwidespreadadoptionofLLM'sformanyrealpur
- GEO数据的下载和处理|GEO数据转换为Gene symbol|GEO注释文件提取symbol|查看样本标签|查看GEO数据疾病或正常|生物信息基础
Red Red
生信小技巧学习笔记生物信息r语言GEO数据库数据库
GEO数据的下载和处理|GEO数据转换为Genesymbol|GEO注释文件提取symbol|查看样本标签|查看GEO数据疾病或正常|生物信息基础数据的下载和处理首先在GEO数据库中通过GSEID找到相关数据,然后下载txt文件。数据读取与处理。#设置工作路径,也就是你的分析数据存放以及要保存到地方setwd(dir="C:\\Users\\LiaoMinzhen\\PycharmProjects
- 史上最全的maven的pom.xml文件详解
Meta999
Maven
注:详解文件中,用红色进行标注的是平常项目中常用的配置节点。要详细学习!转载的,太经典了、、、、欢迎收藏xxxxxxxxxxxx4.0.0xxxxxxjar1.0-SNAPSHOTxxx-mavenhttp://maven.apache.orgAmavenprojecttostudymaven.jirahttp://jira.baidu.com/
[email protected]
- 【网络安全 | 代码审计】JFinal之DenyAccessJsp绕过
秋说
网络安全web安全java代码审计漏洞挖掘
未经许可,不得转载。文章目录前言代码审计推理绕过Tomcat解析JSP总结概念验证阐发前言JFinal是一个基于Java的轻量级MVC框架,用于快速构建Web应用程序。它的设计理念是追求极简、灵活、高效,旨在提高开发效率,减少冗余代码的编写,适合中小型项目以及对性能有较高要求的项目。在较新的JFinal版本中,默认情况下无法直接通过浏览器地址栏输入.jsp文件名来访问对应的JSP文件。也就是说,主
- 【Unity基础】如何选择脚本编译方式Mono和IL2CPP?
tealcwu
Unity基础unity游戏引擎
Edit->ProjectSettings->Player在Unity中,ScriptingBackend决定了项目的脚本编译方式,即如何将C#代码转换为可执行代码。Unity提供了两种主要的ScriptingBackend选项:Mono和IL2CPP。它们之间的区别影响了项目的性能、平台支持、编译时间和调试体验。以下是两者的详细对比:1.Mono简介:Mono是Unity最早使用的脚本后端,基于
- python工程打包成whl文件
机灵巢穴_WitNest
pythonpython开发语言
资料:PackagingPythonProjects—PythonPackagingUserGuide6.Modules—Python3.11.4documentation步骤1.安装打包工具python3-mpipinstallsetuptoolswheeltwine2.更新pip工具python3-mpipinstall--upgradepip3.创建工程结构python_test_packa
- 2020-11-12 写单片机内存的脚本 nc openocd 事务自动测试
linuxScripter
这是写单片机内存的脚本:z@z-ThinkPad-T400:~/zworkT400/EDA_heiche/zREPOgit/simple-gcc-stm32-project$catz.wholeRun.oneCase.cmdcattmp6.toWrite|awk'{system("echomwb"$1""$2"|nclocalhost4444");}'catUSER/DEBUG/debug.h|g
- 压测服务器并使用 Grafana 进行可视化
豆瑞瑞
grafana
简介仓库代码GitCode-全球开发者的开源社区,开源代码托管平台参考Welcome!-TheApacheHTTPServerProjectGrafana|查询、可视化、警报观测平台https://prometheus.io/docs/introduction/overview/
- idea右侧工具栏找不到maven窗口
足球数据分析
intellij-idea
idea没有识别到是maven项目处理方案:右键pom.xml文件,点击"addasmavenproject"
- UnrealEngine学习(03):虚幻引擎术语
依晴无旧
UnrealEngine学习虚幻游戏引擎
1.项目虚幻引擎5项目(UnrealEngine5Project)中包含游戏的所有内容。项目中包含的大量文件夹都在磁盘上,例如Blueprints和Materials。你可以按照自己的意愿命名文件夹并将其整理到项目中。虚幻编辑器(UnrealEditor)中的内容浏览器(ContentBrowser)面板显示与磁盘上的Project文件夹相同的目录结构。每个项目都有与其关联的.uproject文件
- 文件大小自动转换工具类
小卡车555
java
根据传入的文件大小,自动转换为B、KB、MB、GB、TBimportjava.text.DecimalFormat;publicclassFileSizeUtil{/***文件单位*/privatestaticfinalString[]units=newString[]{"B","KB","MB","GB","TB"};/***文件大小自动转换*@paramsize*@return*/public
- 枚举,注解
柴...
韩顺平学习java开发语言
自定义类实现枚举1.不需要提供setXxx方法,因为枚举对象值通常为只读2.对枚举对象/属性使用final+static共同修饰,实现底层优化3.枚举对象名通常使用全部大写,常量的命名规范(XXX_XXX)4.枚举对象根据需要,也可以有多个属性packagechapter;publicclassEnum{publicstaticvoidmain(String[]args){System.out.p
- C#LINQ常用扩展语句
月落.
C#c#linqsolr
在C#中,LINQ提供了许多扩展方法,这些方法定义在System.Linq命名空间中。以下是一些常用的LINQ扩展方法:Where-过滤数据集合,返回满足条件的元素。varfilteredItems=collection.Where(item=>item.SomeProperty>10);Select-从数据集合中选择数据或创建新的投影。varprojectedItems=collection.S
- Java之String、StringBuffer、StringBuilder
zoux
(1)String:String类是final修饰的,是不可变的。我们看到的例如:Stringa="hello";a=a+"1";实际上是先生成了一个对象然后得到结果"hello1",最后在赋值给对象a;String类型的任何改动都是先生成一个其他对象再重新赋值。所以String类适合那种常量或者基本没变化的字符串。(2)StringBuilderStringbuffer是可改变的,用append
- Python中的“Try...Except...Finally”:掌握异常处理的艺术
小鹿( ﹡ˆoˆ﹡ )
Pythonpython开发语言Python
在编程的世界里,错误与异常就像是旅途中的迷雾,虽然不可避免,但通过正确的导航工具,我们可以安全地穿越。Python作为一种广泛使用的编程语言,提供了丰富的工具来帮助我们处理这些异常情况,其中之一便是“Try…Except…Finally”结构。本文将带你深入了解这一机制的核心概念、实际应用以及如何利用它来提升代码的健壮性和可维护性,无论你是刚入门的新手还是经验丰富的开发人员,都能从中受益匪浅。引言
- Celery 立即执行任务 延迟执行任务
i0208
Celerypython
包架构封装project├──celery_task#celery包│├──__init__.py#包文件│├──celery.py#celery连接和配置相关文件,且名字必须交celery.py│└──tasks.py#任务体函数文件├──add_task.py#执行任务脚本文件(这个文件可以在任意位置)└──get_result.py#获取结果注意:任务体代码文件要与celery.py文件在
- Hadoop windows intelij 跑 MR WordCount
piziyang12138
一、软件环境我使用的软件版本如下:IntellijIdea2017.1Maven3.3.9Hadoop分布式环境二、创建maven工程打开Idea,file->new->Project,左侧面板选择maven工程。(如果只跑MapReduce创建java工程即可,不用勾选Creatfromarchetype,如果想创建web工程或者使用骨架可以勾选)image.png设置GroupId和Artif
- Java面试必问之Hashmap底层实现原理(JDK1.7)
当我遇上你csy
Java基础javahashmap面试源码
1.前言Hashmap可以说是Java面试必问的,一般的面试题会问:Hashmap有哪些特性?Hashmap底层实现原理(get\put\resize)Hashmap怎么解决hash冲突?Hashmap是线程安全的吗?…今天就从源码角度一探究竟。笔者的源码是OpenJDK1.72.构造方法首先看构造方法的源码//默认初始容量staticfinalintDEFAULT_INITIAL_CAPACIT
- idea 启动tomcat 工程_使用IDEA创建JavaWeb项目 部署本地tomcat并运行
心在天上脚在地上
idea启动tomcat工程
一、下载商业版IDEA二、新建JavaWeb项目1、在菜单栏找到File>>New>>Project2、在弹出的窗口中找到JavaEnterPrise>>WebApplication,点击Next3、填写项目名称,选择项目位置,然后Finish4、在左侧窗口可以看到IDEA创建JavaWeb工程的目录结构,在src中写java代码,在web目录下放jsp页面。三、下载tomacat下载完成后,解压
- 自动生成不重复的订单id
负熵流
开发语言java
@ApiModel(value="订单")@Entity@EntityListeners(AuditingEntityListener.class)publicclassOrderimplementsSerializable{privatestaticfinallongserialVersionUID=-44480262996409913L;@Id@Column(name="id",nullabl
- 探索.NET Core的宝库:开源项目的无限可能
胡易黎Nicole
探索.NETCore的宝库:开源项目的无限可能awesome-dotnet-core-applicationsAnawesomecollectionof.NETCorerealtime,sample,architecturereferenceapplicationprojects项目地址:https://gitcode.com/gh_mirrors/aw/awesome-dotnet-core-a
- First page
Simon_Liu
Now,finallystarted.NotsurehowlongIcankeepthisup,hopefullylongenough.
- 搭建第一个SpringDataJPA工程
码来码去(未来可期)
JavaWebjava
第一步:创建maven工程,导入maven坐标使用SpringDataJPA,需要整合Spring与SpringDataJPA,并且需要提供JPA的服务提供者hibernate,所以需要导入spring相关坐标,hibernate坐标,数据库驱动坐标等4.2.4.RELEASE5.0.7.Final1.6.61.2.120.9.1.25.1.6junitjunit4.9testorg.aspect
- 请假代码java web_学生请假管理系统
喵灵魂
请假代码javaweb
文件名大小更新时间学生请假管理系统02019-05-31学生请假管理系统\Leave_System02019-05-31学生请假管理系统\Leave_System\.classpath9092019-05-01学生请假管理系统\Leave_System\.project9122019-04-29学生请假管理系统\Leave_System\.settings02019-05-31学生请假管理系统\L
- Tomato and egg noodles
EHHHA
First,washandcutupthetomato.Next,pourtheeggintothebowlThen,potthenoodlesintothepot.Next,putthenoodlesandeggsintothepot.waitfiveminutes.Finaly,putthenoodlesinit.Don'tforgetaddsomesalt.andwecaneatit.图片发
- Axure RP 9 超级教程:自适应视图(Adaptive View Set)
凡间萌宠
本文适用于(非)汉化版AxureRP9自适应视图入门操作废话不表,直接如题。以下为详细步骤:1.新建页面,名称自定,如“自适应”。新建页面2.选择Project下的AdaptiveViewSets...项。选择AdaptiveViewSets3.弹出自适应设置框,点击“+Add”自适应设置框4.弹出新增自适应页面:新增自适应页面5.点击Presets(预制),弹出不同平台以及不同型号大小的显示规格
- Java实现的基于模板的网页结构化信息精准抽取组件:HtmlExtractor
yangshangchuan
信息抽取HtmlExtractor精准抽取信息采集
HtmlExtractor是一个Java实现的基于模板的网页结构化信息精准抽取组件,本身并不包含爬虫功能,但可被爬虫或其他程序调用以便更精准地对网页结构化信息进行抽取。
HtmlExtractor是为大规模分布式环境设计的,采用主从架构,主节点负责维护抽取规则,从节点向主节点请求抽取规则,当抽取规则发生变化,主节点主动通知从节点,从而能实现抽取规则变化之后的实时动态生效。
如
- java编程思想 -- 多态
百合不是茶
java多态详解
一: 向上转型和向下转型
面向对象中的转型只会发生在有继承关系的子类和父类中(接口的实现也包括在这里)。父类:人 子类:男人向上转型: Person p = new Man() ; //向上转型不需要强制类型转化向下转型: Man man =
- [自动数据处理]稳扎稳打,逐步形成自有ADP系统体系
comsci
dp
对于国内的IT行业来讲,虽然我们已经有了"两弹一星",在局部领域形成了自己独有的技术特征,并初步摆脱了国外的控制...但是前面的路还很长....
首先是我们的自动数据处理系统还无法处理很多高级工程...中等规模的拓扑分析系统也没有完成,更加复杂的
- storm 自定义 日志文件
商人shang
stormclusterlogback
Storm中的日志级级别默认为INFO,并且,日志文件是根据worker号来进行区分的,这样,同一个log文件中的信息不一定是一个业务的,这样就会有以下两个需求出现:
1. 想要进行一些调试信息的输出
2. 调试信息或者业务日志信息想要输出到一些固定的文件中
不要怕,不要烦恼,其实Storm已经提供了这样的支持,可以通过自定义logback 下的 cluster.xml 来输
- Extjs3 SpringMVC使用 @RequestBody 标签问题记录
21jhf
springMVC使用 @RequestBody(required = false) UserVO userInfo
传递json对象数据,往往会出现http 415,400,500等错误,总结一下需要使用ajax提交json数据才行,ajax提交使用proxy,参数为jsonData,不能为params;另外,需要设置Content-type属性为json,代码如下:
(由于使用了父类aaa
- 一些排错方法
文强chu
方法
1、java.lang.IllegalStateException: Class invariant violation
at org.apache.log4j.LogManager.getLoggerRepository(LogManager.java:199)at org.apache.log4j.LogManager.getLogger(LogManager.java:228)
at o
- Swing中文件恢复我觉得很难
小桔子
swing
我那个草了!老大怎么回事,怎么做项目评估的?只会说相信你可以做的,试一下,有的是时间!
用java开发一个图文处理工具,类似word,任意位置插入、拖动、删除图片以及文本等。文本框、流程图等,数据保存数据库,其余可保存pdf格式。ok,姐姐千辛万苦,
- php 文件操作
aichenglong
PHP读取文件写入文件
1 写入文件
@$fp=fopen("$DOCUMENT_ROOT/order.txt", "ab");
if(!$fp){
echo "open file error" ;
exit;
}
$outputstring="date:"." \t tire:".$tire."
- MySQL的btree索引和hash索引的区别
AILIKES
数据结构mysql算法
Hash 索引结构的特殊性,其 检索效率非常高,索引的检索可以一次定位,不像B-Tree 索引需要从根节点到枝节点,最后才能访问到页节点这样多次的IO访问,所以 Hash 索引的查询效率要远高于 B-Tree 索引。
可能很多人又有疑问了,既然 Hash 索引的效率要比 B-Tree 高很多,为什么大家不都用 Hash 索引而还要使用 B-Tree 索引呢
- JAVA的抽象--- 接口 --实现
百合不是茶
抽象 接口 实现接口
//抽象 类 ,方法
//定义一个公共抽象的类 ,并在类中定义一个抽象的方法体
抽象的定义使用abstract
abstract class A 定义一个抽象类 例如:
//定义一个基类
public abstract class A{
//抽象类不能用来实例化,只能用来继承
//
- JS变量作用域实例
bijian1013
作用域
<script>
var scope='hello';
function a(){
console.log(scope); //undefined
var scope='world';
console.log(scope); //world
console.log(b);
- TDD实践(二)
bijian1013
javaTDD
实践题目:分解质因数
Step1:
单元测试:
package com.bijian.study.factor.test;
import java.util.Arrays;
import junit.framework.Assert;
import org.junit.Before;
import org.junit.Test;
import com.bijian.
- [MongoDB学习笔记一]MongoDB主从复制
bit1129
mongodb
MongoDB称为分布式数据库,主要原因是1.基于副本集的数据备份, 2.基于切片的数据扩容。副本集解决数据的读写性能问题,切片解决了MongoDB的数据扩容问题。
事实上,MongoDB提供了主从复制和副本复制两种备份方式,在MongoDB的主从复制和副本复制集群环境中,只有一台作为主服务器,另外一台或者多台服务器作为从服务器。 本文介绍MongoDB的主从复制模式,需要指明
- 【HBase五】Java API操作HBase
bit1129
hbase
import java.io.IOException;
import org.apache.hadoop.conf.Configuration;
import org.apache.hadoop.hbase.HBaseConfiguration;
import org.apache.hadoop.hbase.HColumnDescriptor;
import org.apache.ha
- python调用zabbix api接口实时展示数据
ronin47
zabbix api接口来进行展示。经过思考之后,计划获取如下内容: 1、 获得认证密钥 2、 获取zabbix所有的主机组 3、 获取单个组下的所有主机 4、 获取某个主机下的所有监控项
- jsp取得绝对路径
byalias
绝对路径
在JavaWeb开发中,常使用绝对路径的方式来引入JavaScript和CSS文件,这样可以避免因为目录变动导致引入文件找不到的情况,常用的做法如下:
一、使用${pageContext.request.contextPath}
代码” ${pageContext.request.contextPath}”的作用是取出部署的应用程序名,这样不管如何部署,所用路径都是正确的。
- Java定时任务调度:用ExecutorService取代Timer
bylijinnan
java
《Java并发编程实战》一书提到的用ExecutorService取代Java Timer有几个理由,我认为其中最重要的理由是:
如果TimerTask抛出未检查的异常,Timer将会产生无法预料的行为。Timer线程并不捕获异常,所以 TimerTask抛出的未检查的异常会终止timer线程。这种情况下,Timer也不会再重新恢复线程的执行了;它错误的认为整个Timer都被取消了。此时,已经被
- SQL 优化原则
chicony
sql
一、问题的提出
在应用系统开发初期,由于开发数据库数据比较少,对于查询SQL语句,复杂视图的的编写等体会不出SQL语句各种写法的性能优劣,但是如果将应用系统提交实际应用后,随着数据库中数据的增加,系统的响应速度就成为目前系统需要解决的最主要的问题之一。系统优化中一个很重要的方面就是SQL语句的优化。对于海量数据,劣质SQL语句和优质SQL语句之间的速度差别可以达到上百倍,可见对于一个系统
- java 线程弹球小游戏
CrazyMizzz
java游戏
最近java学到线程,于是做了一个线程弹球的小游戏,不过还没完善
这里是提纲
1.线程弹球游戏实现
1.实现界面需要使用哪些API类
JFrame
JPanel
JButton
FlowLayout
Graphics2D
Thread
Color
ActionListener
ActionEvent
MouseListener
Mouse
- hadoop jps出现process information unavailable提示解决办法
daizj
hadoopjps
hadoop jps出现process information unavailable提示解决办法
jps时出现如下信息:
3019 -- process information unavailable3053 -- process information unavailable2985 -- process information unavailable2917 --
- PHP图片水印缩放类实现
dcj3sjt126com
PHP
<?php
class Image{
private $path;
function __construct($path='./'){
$this->path=rtrim($path,'/').'/';
}
//水印函数,参数:背景图,水印图,位置,前缀,TMD透明度
public function water($b,$l,$pos
- IOS控件学习:UILabel常用属性与用法
dcj3sjt126com
iosUILabel
参考网站:
http://shijue.me/show_text/521c396a8ddf876566000007
http://www.tuicool.com/articles/zquENb
http://blog.csdn.net/a451493485/article/details/9454695
http://wiki.eoe.cn/page/iOS_pptl_artile_281
- 完全手动建立maven骨架
eksliang
javaeclipseWeb
建一个 JAVA 项目 :
mvn archetype:create
-DgroupId=com.demo
-DartifactId=App
[-Dversion=0.0.1-SNAPSHOT]
[-Dpackaging=jar]
建一个 web 项目 :
mvn archetype:create
-DgroupId=com.demo
-DartifactId=web-a
- 配置清单
gengzg
配置
1、修改grub启动的内核版本
vi /boot/grub/grub.conf
将default 0改为1
拷贝mt7601Usta.ko到/lib文件夹
拷贝RT2870STA.dat到 /etc/Wireless/RT2870STA/文件夹
拷贝wifiscan到bin文件夹,chmod 775 /bin/wifiscan
拷贝wifiget.sh到bin文件夹,chm
- Windows端口被占用处理方法
huqiji
windows
以下文章主要以80端口号为例,如果想知道其他的端口号也可以使用该方法..........................1、在windows下如何查看80端口占用情况?是被哪个进程占用?如何终止等. 这里主要是用到windows下的DOS工具,点击"开始"--"运行",输入&
- 开源ckplayer 网页播放器, 跨平台(html5, mobile),flv, f4v, mp4, rtmp协议. webm, ogg, m3u8 !
天梯梦
mobile
CKplayer,其全称为超酷flv播放器,它是一款用于网页上播放视频的软件,支持的格式有:http协议上的flv,f4v,mp4格式,同时支持rtmp视频流格 式播放,此播放器的特点在于用户可以自己定义播放器的风格,诸如播放/暂停按钮,静音按钮,全屏按钮都是以外部图片接口形式调用,用户根据自己的需要制作 出播放器风格所需要使用的各个按钮图片然后替换掉原始风格里相应的图片就可以制作出自己的风格了,
- 简单工厂设计模式
hm4123660
java工厂设计模式简单工厂模式
简单工厂模式(Simple Factory Pattern)属于类的创新型模式,又叫静态工厂方法模式。是通过专门定义一个类来负责创建其他类的实例,被创建的实例通常都具有共同的父类。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工厂模式是工厂模式家族中最简单实用的模式,可以理解为是不同工厂模式的一个特殊实现。
- maven笔记
zhb8015
maven
跳过测试阶段:
mvn package -DskipTests
临时性跳过测试代码的编译:
mvn package -Dmaven.test.skip=true
maven.test.skip同时控制maven-compiler-plugin和maven-surefire-plugin两个插件的行为,即跳过编译,又跳过测试。
指定测试类
mvn test
- 非mapreduce生成Hfile,然后导入hbase当中
Stark_Summer
maphbasereduceHfilepath实例
最近一个群友的boss让研究hbase,让hbase的入库速度达到5w+/s,这可愁死了,4台个人电脑组成的集群,多线程入库调了好久,速度也才1w左右,都没有达到理想的那种速度,然后就想到了这种方式,但是网上多是用mapreduce来实现入库,而现在的需求是实时入库,不生成文件了,所以就只能自己用代码实现了,但是网上查了很多资料都没有查到,最后在一个网友的指引下,看了源码,最后找到了生成Hfile
- jsp web tomcat 编码问题
王新春
tomcatjsppageEncode
今天配置jsp项目在tomcat上,windows上正常,而linux上显示乱码,最后定位原因为tomcat 的server.xml 文件的配置,添加 URIEncoding 属性:
<Connector port="8080" protocol="HTTP/1.1"
connectionTi