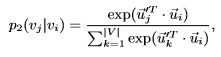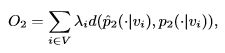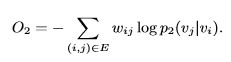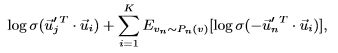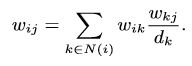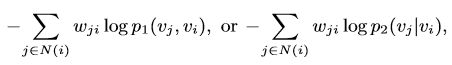LINE:Large-scale Information Network Embedding

论文信息

发表:
2015年的WWW会议上
作者：
  Jian Tang ,Microsoft Research Asia, Beijing, China
  Meng Qu ,Peking University, Beijing, China
  Mingzhe Wang ,Peking University, Beijing, China
  Ming Zhang ,Peking University, Beijing, China
  Jun Yan ,Microsoft Research Asia, Beijing, China
  Qiaozhu Mei ,University of Michigan, Ann Arbor, MI, USA
摘要：
  本文研究了将大规模信息网络embedding到低维向量空间中的问题，这对于可视化，节点分类和链接预测等许多任务是非常有用的。大多数现有的graph embedding方法不能用于通常包含数百万个节点的真实世界信息网络。在本文中，我们提出了一种新的network embedding方法，称为“LINE”，适用于任意类型的信息网络：无向、有向和有权、无权。该方法优化了精心设计的目标函数，能够保留局部和全局网络结构。提出了边缘采样算法，解决了经典随机梯度下降的局限性，提高了算法的有效性和效率。经验实验证明了LINE在各种现实世界信息网络（包括语言网络，社交网络和引用网络）上的有效性。该算法非常高效，能够在典型的单机上在几个小时内学习数百万个顶点和数十亿条边的网络。
代码：
https://github.com/tangjianpku/LINE

背景

1. 信息网络在现实世界中无处不在，例如航空公司网络，出版网络，社交和通信网络以及万维网。这些信息网络的规模从几百个节点到数十亿个节点。分析大型信息网络已经引起学术界和工业界越来越多的关注。
2. 为了分析信息网络，可以通过graph embedding的方法。Graph embedding在可视化、节点分类、链接预测等任务中很有用。但是现有的graph embedding算法，有些在规模较小的网络上表现很好，在现实网络（大规模网络）中的表现差强人意；有些不是针对网络设计的，或没有明确的目标函数。
   graph embedding（node embedding）:将图中的每个节点都表示成一个向量，节点的向量表示形式中要包含图的结构信息，如在网络中相似的点在向量表示中的距离比较近。

算法目标：能够对大规模信息网络进行graph embedding，保证有效性和高效性。

相关工作

• graph factorization
• Deepwalk

后面的实验中，将和这两个算法进行比较。

相关定义

Information Network（信息网络）：一个信息网络被定义为G =（V，E），其中V是顶点集合，每个代表一个数据对象，E是顶点之间的边集，代表两个数据对象之间的关系。 每个边e∈E是一个有序对e =（u，v），并且与权重w_uv> 0相关联，表示关系的强度。 如果G是无向的，则有（u，v）≡（v，u）和w_uv≡w_vu; 如果G是定向的，我们有（u，v）！≡（v，u）和w_uv！≡w_vu。
负权重是有可能的，本实验中不考虑

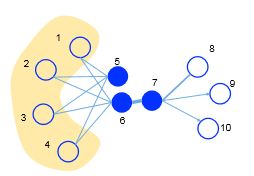
First-order Proximity（一阶相似度）：网络中的一阶相似度是两个顶点之间的自身相似（不考虑其他顶点）。 对于由边（u，v）连接的每一对顶点，边上的权重w_uv表示u和v之间的相似度，如果在u和v之间没有观察到边，则它们的一阶相似度为0。
一阶邻近通常意味着现实世界网络中两个节点的相似性。例如，在社交网络中相互交友的人往往有着相似的兴趣;在万维网上相互链接的页面倾向于谈论类似的话题。

Second-order Proximity（二阶相似度）：网络中一对顶点（u，v）之间的二阶相似度是它们邻近网络结构之间的相似性。 在数学上，设p_u=（w_u，1，...，w_{u，| V |}）表示u与所有其他顶点的一阶相似度，则u和v之间的二阶相似度 由 p_u和p_u决定。 如果没有顶点与u和v都连接，则u和v之间的二阶相似度为0。
因为有些边观察不到等原因，一阶相似度不足以保存网络结构。因此提出共享相似邻居的顶点倾向于彼此相似，即二阶相似度。 例如，在社交网络中，分享相似朋友的人倾向于有相似的兴趣，从而成为朋友; 在词语共现网络中，总是与同一组词语共同出现的词往往具有相似的含义。

图1

因为6和7之间有边，所以6和7一阶相似。因为5和6之间虽然没有边，但是有4个相同的邻居节点，所以5和6二阶相似。

Large-scale Information Network Embedding（大规模网络信息嵌入）：给定一个大的网络G =（V，E），大规模信息网络嵌入问题的目的是将每个顶点v∈V表示成一个低维空间R^d中的向量，即学习一个函数 f_G：V→R^d，其中d<<| V |。 在R^d空间中，顶点之间的一阶相似度和二阶相似度都被保留下来。

算法

输入输出：

  LINE是实现graph embedding的算法，即输入是网络图，输出是网络图中节点的向量表示。

适用范围：

  大规模（百万的顶点和数十亿的边）的任意类型的网络：有向或无向、有权或无权
文章中只提到可以扩展到规模很大的网络，小规模网络应该也可以

只保留一阶相似度的LINE模型

1. 为了模拟一阶相似度，对于每个无向边（i，j），我们定义顶点v_i和v_j之间的联合概率如下：（sigmoid function，向量越接近，点积越大，联合概率越大）
   
   

   (1)
   
   其中，u_i表示节点v_i对应的向量。这样就定义了一个V*V的分布p（·，·）
2. 经验概率可以定义为：（两点之间边的权值越大，经验概率越大）
   
   

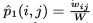   image.png
   
   其中，W=Σw_i。得到了另一个分布。
3. 为了保持一阶相似性，一个简单的办法是最小化下面的目标函数：
   
   

   (2)
   
   其中d（·，·）是两个分布之间的距离。
   我们选择最小化两个概率分布的KL散度，用KL散度代替d（·，·）并省略一些常数，得到：
   
   

   (3)

  可以看出，只考虑一阶相似度的情况下，改变同一条边的方向对于最终结果没有什么影响。因此一阶相似度只能用于无向图，不能用于有向图。

只保留二阶相似度的LINE模型

  二阶相似度可以用于有向图和无向图。下面是针对有向图的算法（在无向图中，可以将每条边看成是两条方向相反且有相同权重的有向边）。
  二阶相似度假设共享邻居的顶点彼此相似。每个顶点扮演两个角色：顶点本身和其他顶点的邻居。因此，为每个节点引入两个向量表示u_i和u_i`：u<sub>i</sub>是v<sub>i</sub>被视为顶点时的表示，u<sub>i</sub>`是当v_i被视为特定邻居时的表示。

1. 定义v_j是v_i的邻居的概率为（v_j和v_i越相似，对应向量点积越大，v_j是v_i的邻居的概率越大，）：
   
   

   (4)
   
   其中，|V|是网络中顶点的数目。方程 （4）定义了一个条件分布p2（·| vi），表明了低维向量空间中，各个点是顶点v_i的邻居的概率。
2. 经验概率（网络中，各个点是v_i的邻居的概率）定义为：
   
   

   image.png
   
   其中w_ij是边（i，j）的权重，d_i是顶点i的出度，d_i=Σ_k∈N(i) w_ik。
3. 二阶相似度假设共享邻居的顶点彼此相似，为了保持二阶相似度，同一个顶点在向量空间中的的条件分布要接近在网络中的条件分布。
   因为网络中顶点的重要性不同，引入λ_i表示网络中顶点的重要程度，可以通过PageRank等算法来度量或估计。
   因此，我们最小化以下目标函数：
   
   

   (5)
   
   为简单起见，将λ_i设置为顶点i的度数，即λi= di。这里也采用KL散度作为距离函数， 用KL散度代替d（·，·）。再省略一些常数，得到：
   
   

   6

结合一阶相似度和二阶相似度

  采用分别训练一阶相似度模型和二阶相似度模型，然后将学习的两个向量表示连接成一个更长的向量。更适合的方法是共同训练一阶相似度和二阶相似度的目标函数，比较复杂，文章中没有实现。

模型优化

1. 负采样
     优化目标（6）计算量太大，在计算条件概率p2（·| vi）时需要对整个顶点集进行求和。 为了解决这个问题，采用负采样方法，根据每个边（i，j）的噪声分布对多个负边进行采样。 更具体地说，它为每个边（i，j）指定了以下目标函数：
   
   

   （7）
   
   其中σ(x) = 1/(1 + exp(−x))是sigmoid函数。 第一项建模观察到的边；第二项建模从噪声分布中得出的负边缘，K是负边缘的数量，设定P_n（v）∝d_v^{3 / 4}，d_v是顶点v的出度。
     对于目标函数（3），存在一个平凡解：u_ik =∞，对于i = 1，...，| V | 和k = 1，...，d。 为了避免平凡解，我们仍然可以利用负采样方法，通过将上式（7）中的u_j`改为u_j。
2. 边采样
     采用异步随机梯度下降算法（ASGD）来进行优化 。如果边（i，j）被采样，则对应的梯度将被计算为：
   
   

   8
   
   因为梯度计算过程中，要乘以边的权重，所以当权重的变化范围很大时，就会导致梯度变化大，很难找到合适的学习率。
     为了解决这一问题，可以将有权边缘展开为多个无权边，例如，具有权重w的边展开为w个无权边。但是展开后，会显著增加内存需求。解决方案为：现在网络中，对边进行采样，采样的概率与边的权重成正比；再将采样后的边展开成无权边。
     这样就可以找到合适的学习率，并且不休要修改目标函数。那么，如何根据权重在网络中对边进行采样呢？LINE采用了别名抽样法。
3. 时间复杂度
     通过别名抽样法采样一个边需要的时间为O(1)；负采样的优化需要O(d(K + 1))时间，其中K是负样本的数量。因此，总体上每个步骤需要O(dK)时间。在实践中，发现用于优化的步数通常与边O(| E |)成正比。因此，LINE的整体时间复杂度为O(dK | E |)，它与边数| E |成线性关系，并且不依赖于顶点数| V |。

FAQ

1. 度数很低的顶点如何处理？
     这样的节点的邻居数量非常少，所以很难精确地推断它的表示，特别是基于二阶相似度的方法。
     解决方案是通过添加更高阶的邻居扩展这些顶点的邻居，例如将节点邻居的邻居作为节点的邻居。LINE中只考虑向每个顶点添加二阶邻居，即邻居的邻居。顶点i与其二阶邻居j之间的权重被测量为：
   
   

   （9）
   
   在实验中，只将集合{j}中w_j最大的一些节点添加到节点i的邻居中。
2. 新加入的顶点如何处理？
     新加入节点i与已有节点的连接已知的情况：可以得到经验分布p₁（·，v_i）和p₂（·| v_i）,然后可以通过最小化下面的任一目标函数得到新节点的向量表示（已有节点的向量表示保持不变）
   
   

   10
   
     新加入节点i与已有节点的连接未知的情况：需要根据新节点的其他信息，如新节点的文本信息，LINE中没有实现。

实验

数据集

1. 语言网络：在词类比任务中从整套英文维基百科页面构建一个词语共现网络。每5个字滑动窗口内的字被认为是共现的，出现频率小于5的词被滤除。在文档分类任务中，使用维基百科界面的摘要，及其对应的类别。
2. 社交网络：使用两个社交网络：Flickr和Youtube。 其中，Flickr网络比Youtube网络（DeepWalk中使用的网络）更密集。
3. 引用网络：使用DBLP数据集来构建作者和文章两个引用网络。作者引用网络中边的权值表示一位作者引用另一位作者的论文数量。

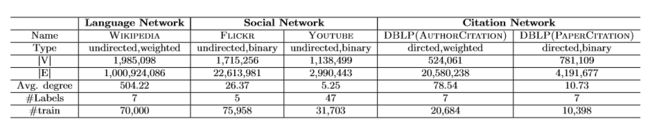
表1是这些网络的详细统计信息：

表1 真实世界信息网络统计信息

比较算法

  只选择了能够扩展到非常大的网络的算法，一些经典算法如MDS，IsoMap和Laplacian eigenmap只能用于小规模网络，因此没有加入比较。

1. Graph factorization (GF)：只适用于无向网络。
2. DeepWalk：只适用于无权边，仅利用二阶相似度。
3. LINE-SGD：没有经过模型优化的LINE算法，包括只考虑一阶相似度（LINE-SGD(1st)）和只考虑二阶相似度（LINE-SGD(2nd)）的两个变体。其中，LINE-SGD(1st)只适用于无向图，LINE-SGD(2nd)适用于各种图。
4. LINE：经过模型优化后的LINE算法，同样包括LINE(1st)和LINE(2nd)两个变体。其中，LINE(1st)只适用于无向图，LINE(2nd)适用于各种图。
5. LINE (1st+2nd)：同时考虑一阶相似度和二阶相似度。将由LINE（1st）和LINE（2nd）学习得到的两个向量表示，连接成一个更长的向量。在连接之后，对维度重新加权以平衡两个表示。因为在无监督的任务中，设定权重很困难，所以只应用于监督学习的场景。
6. Skip-Gram：只能用于语言网络，因此只在对语言网络进行实验时参与对比。

参数设置

1. 将所有算法随机梯度下降的mini-batch size设置为1。
   mini-batch size：每次训练的样本数
2. 学习率的初始值为ρ₀ = 0.025；ρ_t = ρ₀ (1−t/T)，T是mini-batches或边样本的总数。
3. 向量空间的维度在语言网络中设置为200，其他网络 默认情况下设置为128。
4. LINE和LINE-SGD中，负样本数K=5。
   对于LINE(1st) and LINE(2nd)，样本总数T = 100亿；对于GF，样本总数T = 200亿。
   在DeepWalk算法中， 窗口大小win = 10，游走长度t = 40，每个顶点得到γ= 40个游走序列。
5. 所有的算法最后通过设置||w||₂ = 1实现归一化。

定量结果

1. 语言网络

  用算法得到节点的向量表示来对节点进行词类比和文档分类，以此来进行算法评估。

词类比：
  词类比：给定一个单词对（a，b）和一个单词c，任务的目的是发现一个单词d，使得c和d之间的关系类似于a和b之间的关系。例woman-man = queen-king，即woman-man+king=queen。
  在实验中，是通过对a,b,c的向量表示形式进行运算b-a+c得到d的向量表示的。实验中用到了两类词类比：语义和句法，例：woman-man = queen-king是语义上类比，is good=are bed是句法上类比。

实验结果：

表2 维基百科上的词类比结果

实验结果分析：

1. LINE（2nd）优于所有其他方法，这表明，与一阶相似度相比，二阶相似度更好地捕获单词语义。因为二阶相似意味着两个词可以在相同的语境中被替换，对于语义相似来说，这是比一阶相似度更有用的信息。
2. LINE（2nd）优于在维基百科语料库上训练的Skip-Gram算法。原因可能是，语言网络比原始单词序列更好地捕捉单词共现的全局结构。
3. 尽管DeepWalk使用二阶相似度，GF和LINE（1st）都显着优于DeepWalk。这是因为DeepWalk只能用于无权图，只能忽略边的权重，这在语言网络中非常重要。
4. 用SGD直接优化的LINE模型的性能要差得多。因为语言网络中边的权值范围大，从单个数字到数以万计，使得学习过程受到影响。
5. LINE（1st）和LINE（2nd）的运行效率很高，LINE-SGD稍慢。在内存为1T，有40个2.0GHZ的CPU内核，使用16个线程的单个机器运行平台上，两者比图分解至少快10％，比DeepWalk（5倍慢）效率高得多。LINE-SGD稍慢的原因是必须采用阈值切割技术来防止梯度发生爆炸。

文档分类
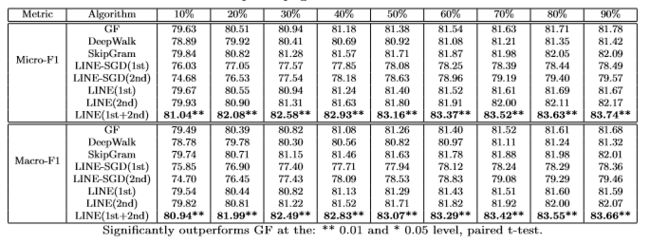
  使用LibLinear软件包，所有的文档向量都被用来训练一个vs-rest逻辑回归分类器。我们的目标是用不同的方法来比较单词embedding，因此取文档中的单词向量表示的平均值作为文档向量。在实验中，随机抽取不同百分比的有标签的文件进行训练，其余的则用于评估， 结果在10次不同的运行中取平均值。。分类指标使用了Micro-F1和Macro-F1。

实验结果：

表3 维基百科界面分类结果

实验结果分析：

1. LINE-SGD表现最差。因为语言网络中边的权值范围大，从单个数字到数以万计，使得学习过程受到影响。
2. DeepWalk表现也比较.因为没有考虑边的权重。
3. LINE(2nd)优于LINE(1st)，略好于图分解。
4. LINE(1st + 2nd)方法最好。这表明一阶和二阶近似是互补的。因为是监督任务，所以将LINE（1st）和LINE（2nd）学习的嵌入连接起来是可行的。

  为了更直观的理解一阶相似和二阶相似，表4比较了使用一阶和二阶相似得到的给定词的最相似的词。

表4 使用一阶相似度和二阶相似度得到的相似词的对比

可以看出，因为使用上下文相似性，由二阶相似度返回的最相似的单词都是语义相关的单词；’由一级相似度返回的最相似的单词是语法和语义相关的单词的混合体。

2. 社交网络

  与语言网络相比，社交网络更加稀疏，特别是Youtube网络。 因此，将每个节点分配到一个或多个社区，通过多标签分类任务来评估算法。 实验中，随机抽样不同比例的顶点进行训练，其余部分用于评估，结果在10次不同的运行中取平均值。

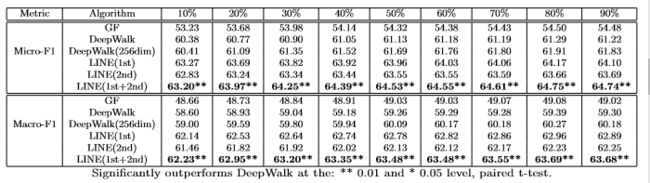
Flicker网络：

实验结果：

表5 Flicker网络多标签分类实验结果

实验结果分析：

1. LINE（1st + 2nd）再次胜过所有其他方法。通过连接LINE(1st)和LINE(2nd)的表示，性能进一步提高，证实两个相似是互补的
2. LINE(1st)略好于LINE(2nd)，这与语​​言网络上的结果相反。原因有两点：(1)社交网络中的一阶相似性比二阶相似性更重要; (2)当网络太稀疏,节点的平均邻居数量太小时，二阶邻近可能变得不准确。
3. LINE(1st)胜过图分解。这表明更好的模拟一阶相似性。
4. LINE(2nd)胜过DeepWalk。这表明更好的建模二阶相似。

YouTube网络：
因为YouTube网络非常稀疏，节点的平均度数低至5。-除了在原图上进行实验外，还重构了新的网络进行实验。在重构图中，为了丰富节点的邻居，使用广度优先搜索策略扩展每个顶点的邻域，即递归地添加邻居的邻居，直到扩展邻域的大小达到1000个节点。

实验结果：

表6 在Youtube网络上进行多标签分类的结果，括号中的是重构网络上的结果

实验结果分析：

1. 原图中，LINE(1st)大多数情况下优于LINE(2nd)。原因与Flicker网络中一样。
2. 原图中，LINE(2nd)的性能逊色于DeepWalk.这是因为网络太稀疏。
3. 原图中，LINE(1st+2nd)的性能优于DeepWalk。表明两个近似是相互补充的，能够解决网络问题稀疏。
4. 重构网络中，GF，LINE(1st)和LINE(2nd)的表现都有所提高，特别是LINE(2nd)，LINE（1st + 2nd）的性能并没有太大的提高。这意味着原始网络上一阶和二阶相似的组合已经获得了大部分信息，LINE(1st + 2nd)方法对于网络嵌入是一个非常有效和高效的方法，适用于密集和稀疏网络。
5. 重构网络中，LINE（2nd）在大多数情况下胜过DeepWalk。

3. 引用网络

  GF和LINE方法只适用于无向图，实验中的引用网络都是有向图，因此不参与比较。实验中，只比较DeepWalk和LINE(2nd)。
  实验中也通过多标签分类任务来评估顶点嵌入。发布在会议上发表的会议或论文中的作者被认为属于与会议相对应的类别。

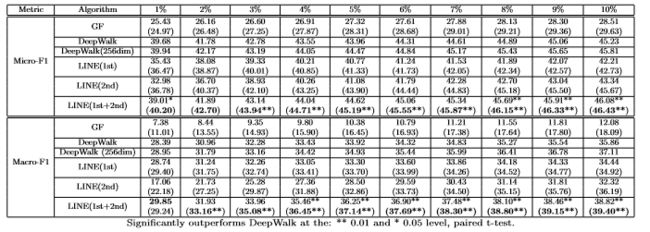
DBLP(Author Citation)网络

实验结果：

表7 对DBLP（AuthorCitation）网络进行多标签分类的结果

实验结果分析：

1. 原网络中DeepWalk胜过LINE(2nd)；网络通过增加度数比较小（小于500）的顶点的邻居来重建网络后，LINE(2nd)的性能显着增加，并且胜过DeepWalk。因为原网络比较稀疏。
2. 使用随机梯度下降LINE(2nd)性能不如预期。

DBLP(PaperCitation)网络

实验结果：

表8 对DBLP（PaperCitation）网络进行多标签分类的结果

实验结果分析：

1. LINE(2nd)明显优于DeepWalk。这是因为引文网络上的随机游走只能沿着引用路径到达之前的论文，并且不能到达其他参考文献；相反，使用LINE(2nd)得到的向量表示中，含有其引用的每个论文参考资料，显然更合理。
2. 当网络通过增加度数比较小（小于200）的顶点的邻居来重建网络时，LINE(2nd)的性能得到进一步改善。

网络布局

  Network Embedding的一个重要应用是在二维空间上实现有意义的可视化。实验中对从DBLP数据中提取的作者共现网络（共同完成过论文的作者之间有边）进行可视化。

网络构建：
  从三个不同的研究领域中选择一些会议：“数据挖掘”中的WWW、KDD，“机器学习”中的NIPS、ICML，以及“计算机视觉”中的CVPR、ICCV。作者来源于这些会议，去掉度数小于3的作者，最终得到18,561位作者和207,074条边缘。
首先使用不同的嵌入方法将合作网络映射到一个低维空间，然后用t-SNE包进一步将顶点的低维向量映射到二维空间。

实验方案：
  首先使用不同的embedding算法将共现网络embedding到一个低维空间，然后用t-SNE包进一步将顶点的低维向量映射到二维空间。

实验结果：

图2 共现的可视化。使用t-SNE包，用embedding作为输入，将作者映射到二维空间。节点的颜色表示作者的社区，红色：“数据挖掘”，蓝色：“机器学习”，绿色：“计算机视觉”。

结果分析：

1. 使用图分解的可视化并不十分有意义，属于同一社区的作者并不聚集在一起。
2. DeepWalk的效果要好得多，但是许多属于不同社区的作者紧紧聚集在中心区域，其中大部分是度数比较高的顶点。这是因为DeepWalk使用随机游走的方法来扩展顶点的邻居，由于随机性，会对度数比较高的顶点带来很多噪音。
3. LINE（2nd）执行得相当好，并生成有意义的网络布局（相同颜色的节点分布得更近）。

在稀疏网络上的表现

1. 从Flickr网络中随机选择不同的百分比的连接，来构建具有不同稀疏程度的网络，来观察网络的稀疏性如何影响LINE(1st)和LINE(2nd)。图3（a）展现了实验结果。

2. 将原始和重建的Youtube网络中的节点根据度数大小分为不同的组，包括(0,1]，[2,3]，[4,6]，[7,12]，[13,30]，[31,+∞)，然后进行评估。图3(b)显示了实验结果。
   

   图3 在稀疏网络中的表现

  通过图(a)可以看出一开始网络非常稀疏时，LINE（1st）优于LINE（2nd）。随着逐渐增加连接的百分比，LINE(2nd)开始超过LINE(1st)。这表明，二阶相似度不适用于网络非常稀疏的情况；当节点有足够的邻居时，它比一阶相似度更好。

  通过图(b)可以看出：(1).在原始网络中，除第一组外，LINE(2nd)优于LINE(1st)。这证明二阶相似度对度数低的节点不起作用。(2).在重构密集网络中，LINE(1st)和LINE(2nd)的性能都得到改善，特别是保持二阶相似度的LINE(2nd)。(3).重构网络上的LINE(2nd)模型在所有组中均优于DeepWalk。

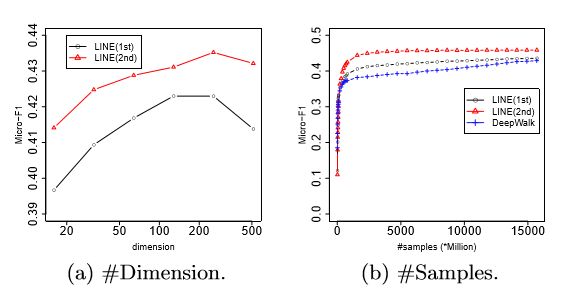
参数灵敏度

  研究算法在不同维度d下的表现，图4(a)展现了实验结果；以及重建的Youtube网络上，不同样本数量对算法的收敛性的影响,图4(b)展现了实验结果。

图4 对维度和样本数目的敏感度

  通过图4(a)可以看出，当维度过大时，LINE(1st)或LINE(2nd)的性能下降。通过图4(b)可以看出,LINE(2nd)始终优于LINE(1st)和DeepWalk，LINE(1st)和LINE(2nd)的收敛速度比DeepWalk快得多。

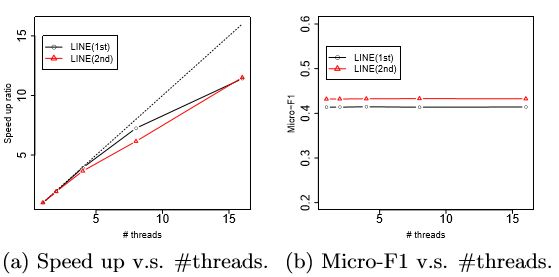
可扩展性

  最后，论文中研究了通过边采样处理和异步随机梯度下降进行优化的LINE模型的可扩展性，LINE中部署多个线程用于优化。

图5 多线程下的表现

  图5(a)显示了在Youtube数据集上进行运算时，线程数对速度的影响，可以看出加速非常接近线性。通过图5(b)可以看出，使用多个线程进行更新时，分类性能保持稳定。这两个图形一起表明，LINE模型的相关算法是可扩展的。

总结

  本文提出了一种称为“LINE”的新型node embedding模型，它可以很容易地扩展到具有数百万个顶点和数十亿边缘的网络。它精心设计的目标函数保留了一阶和二阶的相似性，这些相似性是互补的。针对模型提出了一种有效的边抽样方法，解决了加权边缘随机梯度下降的局限性，同时又不影响效率。各种实际网络的实验结果证明了LINE的高效性和有效性。