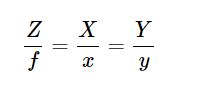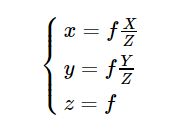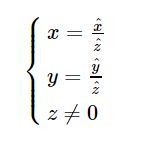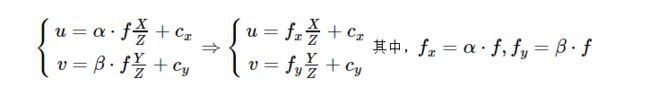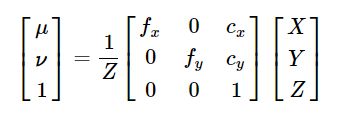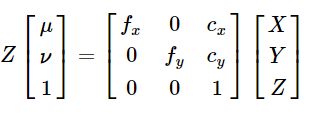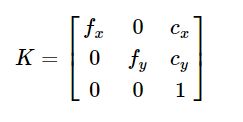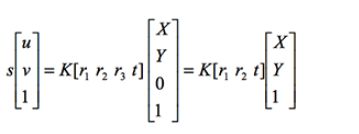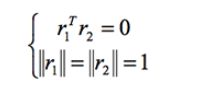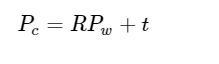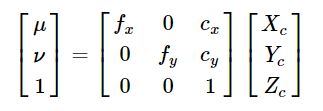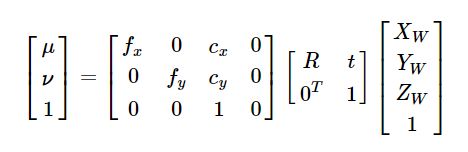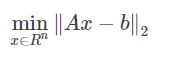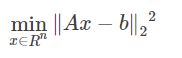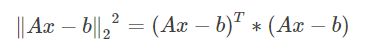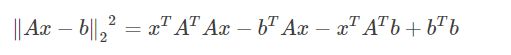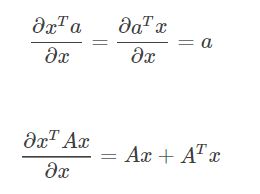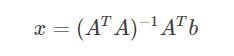（1-1）相机成像模型

 

https://www.cnblogs.com/wangguchangqing/p/8126333.html

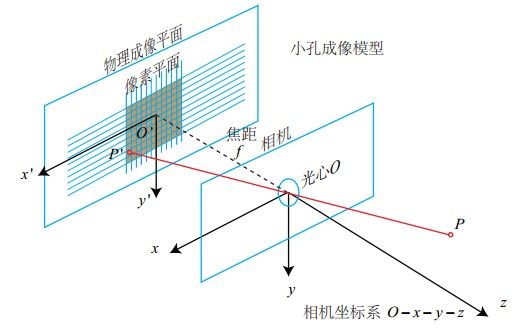
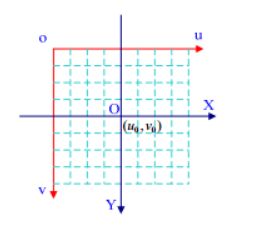
小孔成像模型

 

 

 

 

 

 

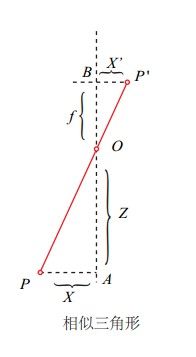
 由上图根据三角形的相似关系，可以得到如下公式：

 

 

 

 将上面公式整理后可以得到：

 

 

 

上面的公式就描述了三位空间到二维平面的映射，但是该映射对于坐标Z来说却是非线性（作为分母），通过上面的公式方便的统一处理X,Y,ZX,Y,Z这三个坐标轴的数据。就需要引入新的坐标（扩展坐标的维度）将其线性化，如下：

 

 

 

  ------- 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 将上面的公式写为齐次坐标的形式：

 

 

 

 通过上面的的推导，就得到了相机的内参数矩阵（Camera Intrinsics）K，

 

 

 

 

 

 

 

 

 

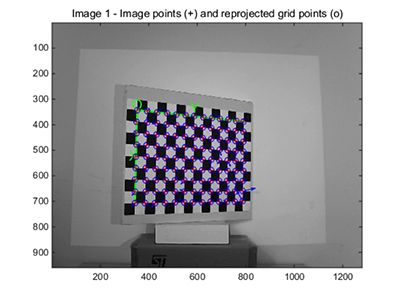
由于棋盘格上所有的角点都位于同一平面上，角点的世界坐标系的Z轴全部取0，即假定模板平面位于世界坐标系Z=0的平面上，因此，旋转矩阵减少一维，得到如下变换：

 

 

 

首先角点在图像上的u v有确定值   在真实世界定义了左上角 00 每个格子的大小是25mm，所以每个点的（X Y Z(未知)）有很多对

 

 

 

 

 

世界坐标旋转R  T

 

 

 令 H=[h1 h2 h3]=K[r1 r2 t]，H即为单应性矩阵，由旋转矩阵R正交性质，有：

 

 

 

 变换一下，可得约束方程：

 

 

 

 

外参数

其中，pp是图像中像点的像素坐标，K是相机的内参数矩阵，P是相机坐标系下的三维点坐标。

 

相机坐标系其会随着相机的移动而改变坐标的原点和各个坐标轴的方向

需要引进一个稳定不变坐标系：世界坐标系，该坐标系是绝对不变

 

其齐次坐标的形式

 将旋转矩阵R和平移向量t带入

 上面就推导得到相机的外参数（Camera Extrinsics）T

 

其中，RR是旋转矩阵，tt是平移向量.

内外参数组合到一起

 

 

 

 

 为了能够和外参数联合，需要将上式齐次化

 

 

 可以将内外参数组合到一起称为相机矩阵，其作用是将真实场景中的三维点投影到二维的成像平面。

 

最小二乘法解的矩阵形式：

 

 

 使得距离最小的向量x与使得距离平方最小的向量x是相同的

=

 

 

 

 

 求最极值问题直接对应的就是导数为零

求导得到：

先验公式

 

 

 

 得到

 

 

 

 

 

 A必须

条件

 

 

 给一个标定板