写在前面:
对Metal技术感兴趣的同学,可以关注我的专题:Metal专辑
也可以关注我个人的账号:张芳涛
所有的代码存储的Github地址是:Metal
正文
Raymarching是一种用于实时图形场景中的快速渲染方法。 通常情况下,几何物体不会传递给渲染器,而是使用Signed Distance Fields (SDF)函数在着色器中创建,这些函数描述点与场景中任何对象的表面之间的最短距离。 如果该点位于对象内,则SDF函数返回负数。 此外,SDF还有其他比较实用的用途:它们允许我们减少Ray Tracing使用的样本数量。 与Ray Tracing类似,使用Raymarching,我们还为视图平面上的每个像素做光线的投影,这些光线可以用于确定是否和物体对象相交。
这两种技术的不同之处在于:通过Ray Tracing方式焦点是经过一些严格的方程组运算得出来的,然而通过Raymarching则不会这么严格,它取的是近似值。使用SDFs函数我们可以沿着光线的方向指导我们追踪到这个物体,最终去确定交点。和通过精确地运算相比,这样的好处是极大地减少了运算量。尤其是当一个场景中物体比较多并且场景比较复杂的时候,那些复杂的运算就显得不太现实。Raymarching另外一个重要的用处是做体积渲染(雾,水,云)。这种场景用Ray Tracing就特别困难实现了,因为所谓的物体相交运算根本无从下手。
我们从第11部分的基础之上来实现今天要实现的效果:渲染光线和物体。我们需要两个结构体来分别描述光线和物体:
struct Ray {
float3 origin;
float3 direction;
Ray(float3 o, float3 d) {
origin = o;
direction = d;
}
};
struct Sphere {
float3 center;
float radius;
Sphere(float3 c, float r) {
center = c;
radius = r;
}
};
和第11部分一样,我们需要一个SDF函数用于计算一个点和物体之间的距离。不过和之前的那个函数不同的是,我们这次的视觉点是沿着光线前行的,所以我们需要使用光线的位置:
float distToSphere(Ray ray, Sphere s) {
return length(ray.origin - s.center) - s.radius;
}
当初的目的是绘制平面图形,计算任一点到圆圈之间的距离(不是球体)
float dist(float2 point, float2 center, float radius) {
return length(point - center) - radius;
}
...
float distToCircle = dist(uv, float2(0.), 0.5);
bool inside = distToCircle < 0.;
output.write(inside ? float4(1.) : float4(0.), gid);
...
接下来,我们需要光线并且沿着光线的方向前进来穿过这个场景,所以,我们需要把最后面的三行代码替换掉。
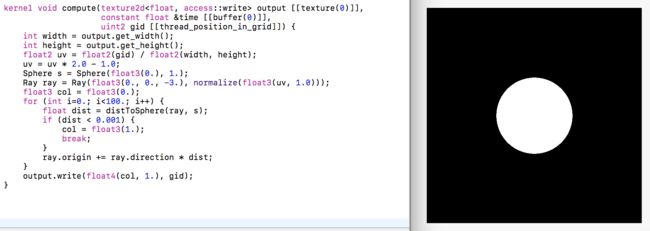
Sphere s = Sphere(float3(0.), 1.);
Ray ray = Ray(float3(0., 0., -3.), normalize(float3(uv, 1.0)));
float3 col = float3(0.);
for (int i=0.; i<100.; i++) {
float dist = distToSphere(ray, s);
if (dist < 0.001) {
col = float3(1.);
break;
}
ray.origin += ray.direction * dist;
}
output.write(float4(col, 1.), gid);
让我们逐行解析一下这些代码:第一步,我们创建了一个球体对象和一条光线对象。这里面需要注意的是,当光线的z坐标接近于0的时候,球体会看起来更大,因为这个时候射线更接近于当前的这个场景。离得越远呢?越小。我们使用我们的射线作为camera(确定视角方向)。第二步,我们将颜色定义为最开始的纯黑色。现在更能从根本上呈现光线传输本质的raymarching出现了。我们需要设定一个for循环的次数(步数)来确保我们可以保证精确度。这次我们先设定100,不过你也可以设成更大的数,其实,精确度越大,性能损耗就越大。在for循环体内部,我们进行从当前位置沿着光线方向到场景之间距离的计算,与此同时,我们还需要检查光线是否和场景之间已经相交,如果已经到达屏幕场景,我们将其设为纯白色并且退出当前循环,否则就把光线往屏幕场景方向靠近,并且更新位置。
需要注意的是:我们将光线方向标准化以覆盖边缘情况,例如矢量的长度(1, 1, 1)(屏幕的一角)的值sqrt(1 * 1 + 1 * 1 + 1 * 1)将近似于1.73。这意味着我们需要将光线的位置向前移动1.73 * dist:这几乎是我们向前移动所需距离的两倍。这样就会导致光线和物体之间无法相交。出于这个原因,我们需要将方向标准化保证其长度一直是1。最后,我们把颜色写入输出纹理。
效果图:
接下来,我们需要创建一个名为distToScene的函数,该函数只是把光线作为一个参数。我们的目的是计算出包含多个对象的复杂场景的最短距离。接下来,在这个新函数中把和球体相关的代码移过来,现在我们只是返回到球体之间的距离。接下来,我们把球体位置的半径改为(1, 1, 1)。0.5意味着这个球体现在在0.5 ... 1.5范围内。这里有一个比较巧妙的技巧来进行实例化:如果我们把空间重复设为0.0 ... 2.0,球体就会安全地进入空间内部。接下来,我们制作射线和模型系数的本地副本。然后,我们使用具有distToSphere()功能的函数来复制光线:
float distToScene(Ray r) {
Sphere s = Sphere(float3(1.), 0.5);
Ray repeatRay = r;
repeatRay.origin = fmod(r.origin, 2.0);
return distToSphere(repeatRay, s);
}
通过使用fmod功能,我们现在可以再整个屏幕填满了空间,而且创建了无数个球体,每一个球体都有自己的射线。当然,我们现在只可以看到屏幕中的x和y范围之内的物体,不过z坐标可以让我看到球体是如何无限深入,我们继续优化代码,把光线移动到一个很远的位置,修改dist距离,再设置一些漂亮的颜色:
Ray ray = Ray(float3(1000.), normalize(float3(uv, 1.0)));
...
float dist = distToScene(ray);
...
output.write(float4(col * abs((ray.origin - 1000.) / 10.0), 1.), gid);
我们用颜色乘以光线的位置。因为场景太大并且在绝大多数地方,光线的位置比1.0要大,这样会导致真个界面白白的,所以我们再除以10。因为屏幕的左侧x小于0会呈现黑色,所以我们需要用到abs()函数。这样我们基本上就可以映射出上下左右边上的颜色。最后,为了匹配我们之前设置的光线原点,我们将光线的位置做一个1000的偏移。
效果图:
接下来,我们需要制作动画效果,在第13部分已经学习到如何发送可用的像time这样的uniforms到GPU。
float3 camPos = float3(1000. + sin(time) + 1., 1000. + cos(time) + 1., time);
Ray ray = Ray(camPos, normalize(float3(uv, 1.)));
...
float3 posRelativeToCamera = ray.origin - camPos;
output.write(float4(col * abs((posRelativeToCamera) / 10.0), 1.), gid);
我们队所有物体的三个坐标都添加了time,但是我们只是让x和y坐标产生波动,让z坐标保持一条直线1.只是防止相机撞到最近的球体而已。
效果图:
代码位置