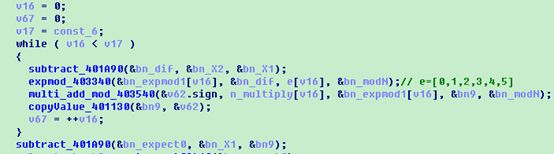
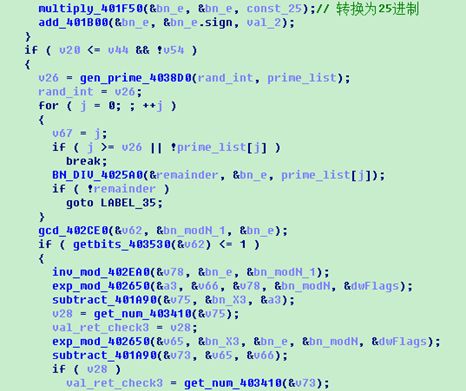
第10题没有反调试,也没有壳,只有复杂的算法,用到了离散对数,素数,模幂等运算,看得头都大了。题目中用到了很多大整数,逆向的基础之一在于怎样确定每个函数的功能?献出我的一个笨方法,弄清楚函数的输入输出参数后,将大数换成数值小的,直接观察它们之间的关系,从而猜出它们间的关系。
譬如:分析sub_402650时,初始运行时第3、4个参数数值过大,不利于分析函数的功能。
00404889 |. E8 C2DDFFFF call 00402650
0014E99C 0018F0B4 //存放结果
0014E9A0 0014EB60 //64
0014E9A4 0014EBDC //8个dword数
0014E9A8 0018F0A8 //7fff…ffed,8个dword
0014E9AC 0014EB0C
我们可以将第3个参数数值改为2,第4个参数数值改为0x111111,发现18F0B4处的结果为0x2710=64^2 mod 0x111111。从而确定sub_402650为幂指取模的运算。
此方法可以广泛应用到该程序的逆向过程中。
此外,为了快速发现数值间的关系,有必要表明大数的结构,在F5出伪代码时,将对应的数据类型改过来。
00000000 BN struc ; (sizeof=0xC, mappedto_35) 00000000 ; XREF: add_401B00/r 00000000 ; sub_401B60/r ...
00000000 sign dd ? ; XREF: add_401B00+3E/w 00000000 ; sub_401B60+3E/w ...
00000004 size_in_dword dd ? ; XREF: add_401B00+31/w 00000004 ; sub_401B60+31/w ...
00000008 pdata dd ? ; XREF: add_401B00+29/w 00000008 ; sub_401B60+29/w ...
0000000C BN ends
sn前半部分、sn后半部分、name这3个关键数据被存储在一个结构中,最后传入到了校验函数final_check_404270中。
00000000 NNN struc ; (sizeof=0x14, mappedto_34) 00000000 ; XREF: sub_403DB0/r
00000000 pdata dd ?
00000004 data_len dd ? ; XREF: sub_403DB0+1FD/o
00000008 str_or_numbase dd ? 0000000C add_num dd ?
00000010 maxcount dd ? 00000014 NNN ends
独立完成这道题时,在分析到0040468F call sub_403410时,卡壳了,往后拉还有那么多黑压压的代码行就胆怯。后来看了大佬们的wp,才明白了该题的思路,总结一下,做个笔记。
sn以XXXX分隔,前半部分即为a,后半部分记为b。
00403B8A call sub_404FB0
后半部分必须为数字,且第一个数字不能为0
00403C5B call _isdigit
.text:00403C3B cmp byte ptr [eax], 30h
.text:00403C3E jz loc_403D76
验证sn,返回结果必须为0
00404004 call final_check_404270
final_check_404270为核心函数,里面有3个判断条件:
第1个条件:
4b
素数N=2^255-19=7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFED
第2个条件:模方程
这里我们令a’=sn前半部分,最后一个字符+0xA,r=b-a’,循环6次的过程如下
sum0 = r^0/N 3*1+0 =3
sum1 = r^1*0/N +sum0/N = 3
sum2 = r^2*1/N +sum1/N =(r^2+3)/N
sum3 = r^3*0/N +sum2/N =(r^2+3)/N
sum4 = r^4*0x40/N +sum3/N = 0X40r^4/N + (r^2+3)/N
sum5 = r^5*0/N +sum4
最后得到的方程
(64r^4/N + (r^2 +3)/N)/n = a
0040468F call get_num_403410
这里我们令x=r^2,这里往回逆的时候要逆两次。化简后可得一个二次模方程。
64x^2 + x +3-a = 0(mod N)
从方程可知,求出a即可反推x,r最后求得b。那么我们继续分析,看如何求a值。
第3个条件:离散对数
1、将sn前半部分最后一位+0x0A,内容转换为0x19进制数,记作E;
2、米勒罗宾素性测试,确保E为素数;
3、 E与(N-1)最大公约数为1
4、检测计算
D = E^-1 mod (N-1)
X = A^D mod N
A = X^E mode N
N=0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFED
这里我们已知A和X的四组数据
'100',0Ah
9230197858975018299629857977411527954550899478307510809210520967346958600039
'101',0Ah
50414221767352083765613498524674590844333823720255656432490557866777248860034
.102',0Ah
38377684164112914669201831650756813551072223314592288217929947158283532270268
'103',0Ah
13436195533519778671648120865743178010431697022400670384909515001970400645091
求D,求离散对数。利用作者dlp工具可以跑出D。
利用作者给出的:基于miracl运算库的 Pollard's kangaroos 方法求离散对数源代码以及编译好可运行的demo
LIMIT64= 95367431640625 , LEAPS= 9765626
solvediscrete logarithm problem - using Pollard's kangaroos
findd in: y = g^d mod n, given(y, g , n),if: d < 64 bits
y=100
g=9230197858975018299629857977411527954550899478307510809210520967346958600039
n=57896044618658097711785492504343953926634992332820282019728792003956564819949
settingtrap ....
trapset! jumps = 9765626
Timecost 18 seconds 362ms
speed531 K/s
Gotcha!Time cost 39 seconds 266 ms
jumps= 21326452, speed = 543 K/s
Discretelog: d =79821823136933
d= 79821823136933=0x4898F769D4A5,将其转换为25进制,最后一个字符-0xA,得出
sn前半部分a为:KCTFREADYK
wolframalpha解方程:
r^2 + 64r^4 + 3 =355419490699766887897429(mod 2**255-19)
解得:
r =1548396171915056368526513804948765619094392315806578106376668805448390390825
故第二部分为:
a’=sn前半部分,最后一个字符+0xA,r=b-a’
a’= 355419490699766887897429
b=1548396171915056368526513804948765619094392315806578106376668805448390390825
+355419490699766887897429
=1548396171915056368526513804948765619094392315806578461796159505215278288254
完整的key:
KCTFREADYKXXXX1548396171915056368526513804948765619094392315806578461796159505215278288254