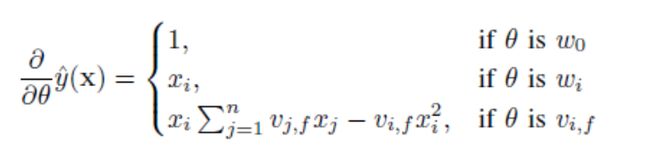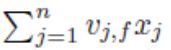理论
FM(Factorization Machine)是由Steffen Rendle在2010年提出,解决了稀疏数据场景下的特征组合问题,在广告,推荐领域被广泛使用.
动机
在高度稀疏的数据场景下如推荐系统,计算广告,传统的线性模型LR,不能很好的学习对应的权重.传统的线性模型,每个特征都是独立的,如果需要考虑特征与特征之间的交互作用,可能需要人工对特征进行交叉组合;非线性SVM可以使用核函数对特征进行映射,但是高维稀疏数据的情况下,不能很好地学习.
高维稀疏数据通常的处理方法是对类别特征进行onehot处理.高维稀疏数据表示一个样本中,非零数很少,绝大部分都是0.如果使用传统的线性模型,特征交互的权重之间是相互独立的,如果说对应的特征交互没有出现相应的样本,就会导致对应权重为0,由于样本的稀疏性,导致了交叉权重有绝大部分均为0.
为什么
那么,FM是如何解决这个问题的?
FM算法模型
模型函数
特征交叉,这里考虑2阶交叉(2-way).对应模型函数为:
其中,w0是全局偏置(如lr模型中b),w是输入特征的参数,
这个函数的前两项就是传统的线性模型,后面一个是交叉特征,这是FM区别于线性模型的地方.
为什么特征交叉对应参数不是直接学习wij,而是通过
因为在稀疏条件下,这样的表示方法打破了特征的独立性,能够更好地挖掘特征之间的相关性.由于数据的稀疏性,如果直接学习xi,xj的交叉特征对应的wij,可能由于xi,xj均为0,导致wij不能被学习.各个wij可以形成一个权重矩阵W,从矩阵分解角度来看,任意正定矩阵W可以分解为VVT.我们通过对V的学习,来近似估计W.同时由于打破了特征独立性,wij表示为
模型计算复杂度
计算复杂度.通过数据变换,可以将复杂度由O(KNN)变为O(K*N).利用2xy = (x+y)2-x2-y^2.
[图片上传失败...(image-369aaa-1573461596043)]
学习方法
对于大多数的损失函数而言,FM里的参数W和V可以通过随机梯度下降SGD来学习,比如logit loss,hinge loss,square loss,模型参数的梯度计算如下:
这部分和样本i是独立的,可以预先计算好.
FM优缺点
优点:
- 在高度稀疏的条件下能够更好地估计交叉特征权重,尤其是对于样本中没有出现的交叉特征;
- FM的参数学习以及样本估计的时间是线性的.使用SGD优化更可行.
- FM是一个通用的模型可以处理任何实值问题.
不足:
- 交叉特征权重计算时,一个xi对应一个vi,表达力不足;同一个特征和其他不同特征交叉时,对应的隐向量表示应该有所区别;
- 模型比较简单,linear regression + 2-way interaction;实际问题中,可能需要更高阶的交叉特征,此时FM学习,表现较差;
代码实现
repo地址: ClickMe