k-NN 算法可以说是最简单的机器学习算法。构建模型只需要保存训练数据集即可。想要对新数据点做出预测,算法会在训练数据集中找到最近的数据点,也就是它的“最近邻”。
1、k近邻分类
k近邻算法最简单的方式就是只有一个最近邻,也就是距离预测数据点最近的训练数据点。如果选择任意的k个近邻时,就会使用“投票法”来指定分类标签。简单点理解,就是在测试数据点周围找寻k个最近邻,然后在这k个最近邻中将出现最多次数分类的类别指向给测试数据。
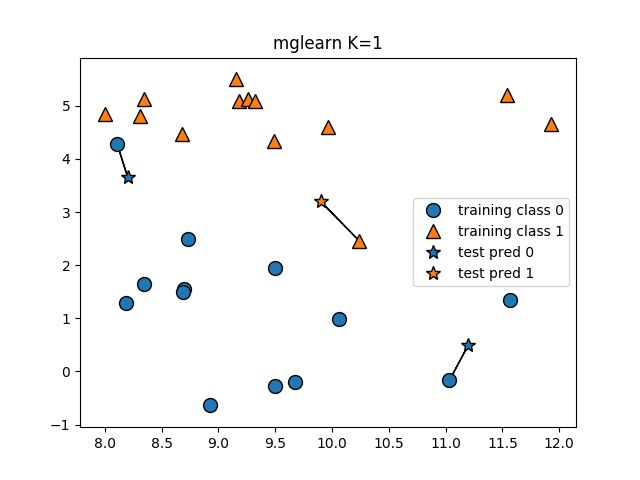
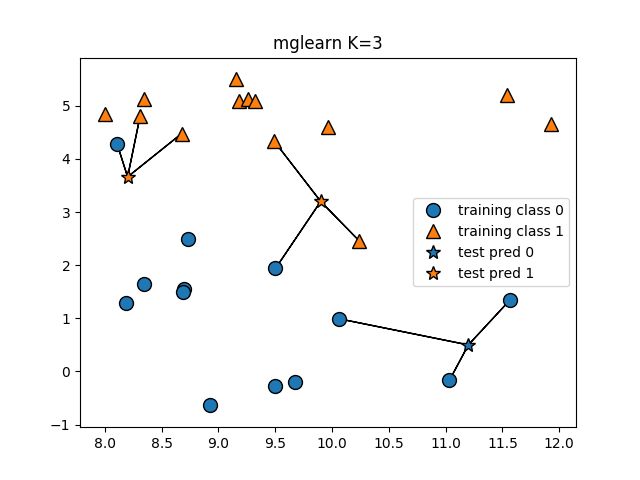
下面展示当k=1的时候,测试点是如何分类的。
import mglearn
import matplotlib.pyplot as plt
# mglearn 的K近邻算法分类
# mglearn.plots.plot_knn_classification
def mglearn_plot_knn_classification(neighbors=1):
mglearn.plots.plot_knn_classification(n_neighbors=neighbors)
plt.title("mglearn K={0}".format(neighbors))
plt.show()
上面的代码,采用的是mglearn包中的KNN算法,接下来换一个,用scikit-learn 来实现
在scikit-learn中,使用的KNeighborsClassifier来实现。上面已经简单说明的kNN算法的思想,接下来我们将数据集中,将测试数据所有可能的预测结果的边界,也就是绘制出0和1两种分类的决策边界。
import mglearn
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
def KNeighborsClassifier_decision_boundary():
X, y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
# fit方法返回对象本身,所以我们可以将实例化和拟合放在一行代码中
clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
# 根据clf绘制决策边界线
mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{} neighbor(s)".format(n_neighbors))
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
axes[0].legend(loc=3)
plt.show()
最后绘制的结果如图:
根据上图,我们发现,当使用的k越小的时候,决策边界越跟着训练数据,也就是完全将测试数据考虑进来,此时的决策边界曲线越复杂,也就是模型越复杂,而k越大的时候,曲线越平滑,模型也就越简单。
而我们使用机器学习,考虑的一个重点就是泛化能力,那么模型越复杂好,还是越简单好呢?而此时的泛化能力对应的又是什么样的呢?
# 模型复杂度和泛化能力的关系
def KNeighborsClassifier_complexity_generalization():
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target,
random_state=66)
training_accuracy = [] # 存放不同neighbors个数对应的训练精度
test_accuracy = [] # 存放不同neighbors个数对应的测试泛化精度
# n_neighbors取值从1到10
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# 构建模型
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
# 记录训练集精度
training_accuracy.append(clf.score(X_train, y_train))
# 记录泛化精度
test_accuracy.append(clf.score(X_test, y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()
plt.show()
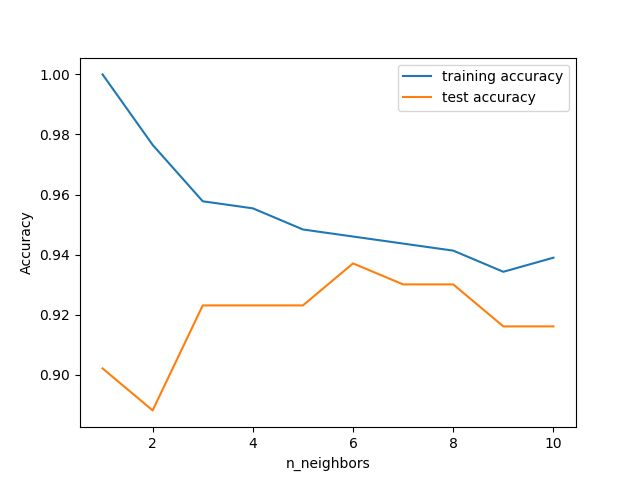
图像的 x 轴是 n_neighbors,y 轴是训练集精度和测试集精度。
通过上图,我们可以得到结论:
考虑单一近邻时,训练集上的预测结果十分完美。
但随着邻居个数的增多,模型变得更简单,训练集精度也随之下降。单 一邻居时的测试集精度比使用更多邻居时要低,这表示单一近邻的模型过于复杂。与之相 反,当考虑10个邻居时,模型又过于简单,性能甚至变得更差。最佳性能在中间的某处,邻居个数大约为 6。
2、K近邻回归
我们也参照上面的例子,先来展示1个和3个近邻时的效果。
# mglearn 的K近邻算法回归
# mglearn.plots.plot_knn_regression
def mglearn_plot_knn_regression(neighbors=1):
mglearn.plots.plot_knn_regression(n_neighbors=neighbors)
plt.show()
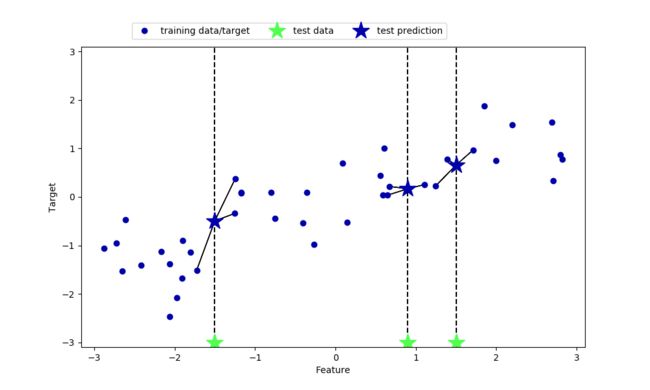
在这里需要说明,与k近邻分类不同的是,测试点的预测结果会根据k的不同,来取最近的K个近邻的平均值作为测试点的预测值,所以这个结果是离散的,并不是已经确定的列表里选择。
在scikit-learn中,使用的KNeighborsRegressor来实现。
# KNeighborsRegressor的分析
def KNeighborsRegressor_analysis():
X, y = mglearn.datasets.make_wave(n_samples=40)
# 将wave数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建1000个数据点,在-3和3之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
# 利用1个、3个或9个邻居分别进行预测
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
ax.set_title(
"{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(n_neighbors, reg.score(X_train, y_train),
reg.score(X_test, y_test)))
ax.set_xlabel("Feature")
ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best")
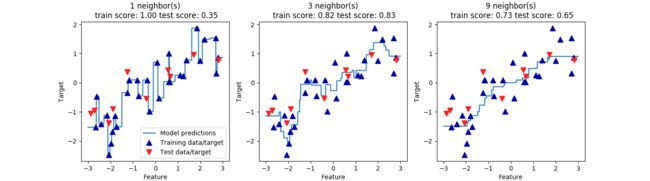
plt.show()
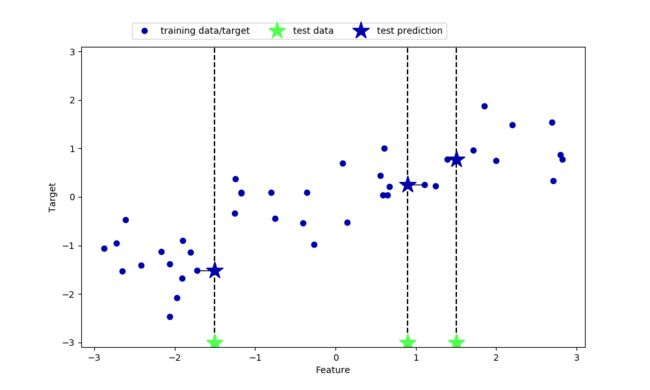
上面的图中,展示的是1,3,9三种k值的情况下,对预测结果的影响。我们看到,当k=1的时候,所有的测试点都对预测结果有影响,即所有预测结果的图像都经过测试点。这样导致预测结果很不稳定。更多的邻居数量后,预测结果的曲线变得更加平滑,但是对数据的拟合就不太好。
3、总结
k-NN模型很容易被理解,而且也不需要过多的调节,仅有的两个重要参数就是k(邻居数量)和距离度量方法(常用的是欧式距离)。
如果训练集很大(特征数很多或者样本数很大),预测速度可能会比较慢。 所以需要对数据进行预处理。同时,对于特征数量很多,或者大多是特征为0的数据集,它的效果也特别不好。