Proof By Simplification
在前面定义数据类型以及函数的时候有使用过Example语句来说明和证明数据的属性。
所使用的证明方法都是一样的:使用关键字simpl来化简等式两边的表达式,然后再使用reflexivity来验证等式两边是否相等。
此外,还可以使用proof by simplification类型的证明方法来证明一些别的属性,证明对所有自然数n,n+0=n:
Theorem plus_O_n : forall n : nat, 0 + n = n. Proof. intros n. simpl. reflexivity. Qed.
需要注意的是,在上面的例子中,关键字simpl并不是必要的,因为reflexivity能够自动完成化简工作,所以上面的证明语句还可以写成:
Theorem plus_O_n' : forall n : nat, 0 + n = n. Proof. intros n. reflexivity. Qed.
此外,reflexivity在简化表达式方面比simpl更加强大,reflexivity会“尝试”展开表达式中的已经定义好了的语句。而simpl和reflexivity之间的差异是:如果reflexivity成功了,那么整个证明目标就完成了,就不需要再看自反性是如何通过简化和展开来扩展表达式的;相比之下,simpl用于可能必须阅读和理解它创建的新目标的情况,因此不希望盲目的展开定义好了的语句而使证明过程变得更加复杂。
关键字Theorem和Example十分相似,但是还是有一些不同之处。
在Theorem中已经添加了量词∀n: nat,因此定理讨论所有自然数n。非正式地,证明定理的形式,形式上通常说“假设n是一些自然数……”,这是由关键字intros n实现的,它将n从目标中的量词移动到当前假设的上下文中。
关键字[intros]、[simpl]以及[reflexivity]就是“策略”的例子,所谓策略就是在Proof...Qed.之间的用于实现证明目标的命令,可以引导程序来检查在前面所作出的假设。
还有一点需要注意的是,[intros]关键字引入变量的顺序和推论中中变量的顺序是保持一致的。
Proof By Rewrite
除了前面所说的建立在对所有的自然数 n, m,上的推论,还有一种建立在满足某个条件的自然数上的推论:
Theorem plus_id_example : forall n m:nat, n = m -> n + n = m + m. Proof. (* move both quantifiers into the context: *) intros n m. (* move the hypothesis into the context: *) intros H. (* rewrite the goal using the hypothesis: *) rewrite -> H. reflexivity. Qed.
上面代码中的第一行关键字[intros],用于普遍量化的变量n,m移入证明的上下文中,这和前面Proof By Simpication中的[intros]关键字的作用一样。
第二行中的[intros H]用于将推论中的假设[n = m]并为其命名为H。
第三行中的关键字[rewrite]用于告诉Coq重写当前目标([n + n = m + m])。将目标中出现的与 H 左边相匹配的字符替换为 H 右边的字符(这与命令中 -> 符号有关,默认是向右的;如果使用 <- 的话,则这条命令会将目标中出现的与H右边匹配的字符替换成H左边的等式)。
关键字[rewrite]不仅可以用于重写假设的内容,还可以重写之前已经证明过了的定理:
Theorem mult_0_plus : forall n m : nat, (0 + n) * m = n * m. Proof. intros n m. rewrite -> plus_O_n. reflexivity. Qed.
在使用[rewrite]时可以指定参数,也就是说指定当前上下文中的变量作为作用在引理上,进而进行重写,如下:
Theorem plus_comm_4 : forall n m p q:nat, n + m + p + q = n + p + m + q. Proof. intros. rewrite <- (plus_assoc (n+m) p q). rewrite <- (plus_assoc n m (p+q)). rewrite (plus_assoc m p q). rewrite (plus_comm m p). rewrite plus_assoc. rewrite plus_assoc. reflexivity. Qed.
需要注意的是,[rewrite]指定重写的变量需要在同一个运算结合等级上,换句话说就是在同一个“括号”内。
Proof By Case Analysis
显而易见,并不是所有的推论都可以通过化简或者重写进行证明。
所以可以使用关键字[destruct]来分情况讨论:
Theorem plus_1_neq_0 : forall n : nat, (n + 1) =? 0 = false. Proof. intros n. destruct n as [| n'] eqn:E. - reflexivity. - reflexivity. Qed.
关键字[destruct]将需要证明的目标分成两个子目标,必须分开证明这两个子目标才能使Coq接受这个推论。
需要注意的是destruct命令中的as [| n'],其中的[| n']的含义是将n分类两种情况进行讨论,而[ ]内用 | 符号分割着两种情况下的自然数构造器的参数:第一种情况没有参数,对应着自然数 O (自然数0);第二种情况的参数为n',因为自然数的构造函数为 S ,所以其对用的自然数为S n'。
上面的分类情况与定义基于自然数类型的递归函数一样。
如果推论中的需要对两个参数进行分情况讨论,也可以采用如下的结构:
Theorem andb_commutative : forall b c, andb b c = andb c b. Proof. intros b c. destruct b eqn:Eb. - destruct c eqn:Ec. + reflexivity. + reflexivity. - destruct c eqn:Ec. + reflexivity. + reflexivity. Qed.
如果需要进行分类讨论的参数的个数有更多个,则需要使用{ }指明分类讨论的范围:
Theorem andb3_exchange : forall b c d, andb (andb b c) d = andb (andb b d) c. Proof. intros b c d. destruct b eqn:Eb. - destruct c eqn:Ec. { destruct d eqn:Ed. - reflexivity. - reflexivity. } { destruct d eqn:Ed. - reflexivity. - reflexivity. } - destruct c eqn:Ec. { destruct d eqn:Ed. - reflexivity. - reflexivity. } { destruct d eqn:Ed. - reflexivity. - reflexivity. } Qed.
但这并不意味着只有当需要分情况讨论的参数大于或等于3个的时候才能使用{ }来指明讨论范围。
如果不想为参数命名,也可以用下面的结构来进行分情况讨论:
Theorem andb_commutative'' : forall b c, andb b c = andb c b. Proof. intros [] []. - reflexivity. - reflexivity. - reflexivity. - reflexivity. Qed.
Proof By Induction
前面所讲的proof by case analysis证明推论的方法实际上就是常见的枚举法,那么相应的,在Coq中也有递归证明的方法,使用关键字[induction]即可实现递归证明:
Theorem mult_1_r : forall n : nat, n * 1 = n. Proof. intros n. induction n as [| n' IHn']. - (* n = 0 *) reflexivity. - (* n = S n' *) simpl. rewrite IHn'. reflexivity. Qed.
通过注释的内容可以理解到,[induction]和[destruct]是的过程是比较相似的:将需要证明的推论分成若干个小的推论,然后分别证明这几个子推论从而使Coq接受这个推论。
在上面的例子中,第一个子推论将[n]替换成[0],没有引入新的变量所以induction中的第一个参数是空的。
在第二个推论中,[n]被替换成[S n'],而有第一个推论得到的子推论n' * 1 = n'被命名为IHn‘并重写进上下文中,然后使用reflexivity进行验证,从而证明了整个推论。
正如前面所讲的那样,[induction]和[destruct]十分相似。所以[induction]也有像[destruct]那样的对多个参数进行递归证明的结构:
Theorem plus_comm_4: forall n m p q : nat, n+m+p+q = n+p+m+q. Proof. intros n m p q. induction n as [| n' IHn']. -induction q as [| q' IHq']. +simpl. rewrite <- plus_n_O. rewrite plus_comm. rewrite <- plus_n_O. reflexivity. +rewrite <- plus_n_Sm. rewrite <- plus_n_Sm. rewrite IHq'. reflexivity. -simpl. rewrite IHn'. reflexivity. Qed.
Proof By Assert
在使用关键字[destruct]的时候,coq会根据分析对象的变量类型的构造器进行分情况讨论,也就是说coq会将原来的证明目标划分成不同情况下的证明目标,产生多个需要证明的子推论,如果这些子推论都能够被证明,那么原来的推论也得到了证明。
但除了通过关键字[destruct]进行分情况讨论将一个推论划分成多个子推论,还可以通过关键字[assert]来构造一个子推论,得到证明后的子推论又和关键字[induction]一样可以在后面的证明直接引用重写:
Theorem plus_swap : forall n m p : nat,
n + (m + p) = m + (n + p).
Proof.
intros n m p.
rewrite plus_assoc.
rewrite plus_assoc.
assert (H:n+m=m+n).
{rewrite plus_comm. reflexivity.
} rewrite H.
reflexivity.
Qed.
也可以在关键字[assert]假设基于新的变量上的推论:
Theorem evenb_S : forall n : nat, evenb (S n) = negb (evenb n). Proof. intros n. induction n as [| n IHn']. -reflexivity. -rewrite IHn'. simpl. assert (H:forall s:bool, negb (negb s)=s). {intros s. destruct s. +reflexivity. +reflexivity. } rewrite H. reflexivity. Qed.
Proof By Replace
关键字[replace]和关键字[assert]其实是差不多的,[replace]用于将当前推论中的某个子表达式替换成另一个表达式,并且将这两个子表达式相等作为一个新的子推论。
即replace (t) with (u),将推论中所有的 t 替换成 u,然后生成一个t = u 的子推论。
Theorem plus_swap' : forall n m p : nat, n + (m + p) = m + (n + p). Proof. intros n m p. rewrite plus_assoc. rewrite plus_assoc. replace (m+n) with (n+m). -reflexivity. -rewrite plus_comm. reflexivity. Qed.
综合实例
有时候需要证明的推论并不能单单用一种证明方法就能证明出来,所以需要将多个证明方法结合使用来进行证明。
而具体应该在什么地方使用何种证明方法,则应该视具体的证明流程而定:
例如,证明下面的推论:
Theorem andb_true_elim2 : forall b c : bool, andb b c = true -> c = true.
显然,要证明上面的推论需要进行分情况讨论:
Proof. intros [] []. -reflexivity. -reflexivity. -reflexivity. -reflexivity. Qed.
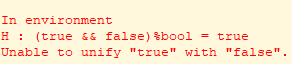
然而,需要证明的推论并不能通过这样的策略得证,下图是运行到第二个case时Coq的运行界面:
也就是说此时Coq只是简单的枚举各种可能的情况,而无视了推论中的假设"andb b c = true",所以无法直接证明该推论;
但正如前面介绍[rewrite]的时候所说的,[rewrite]的字面意思是重写,但实际上却实现了筛选的功能,将满足假设条件的变量筛选出来。
而在证明这个推论的时候,也需要进行筛选:将满足假设条件andb b c = true的变量筛选出来:
Theorem andb_true_elim2 : forall b c : bool, andb b c = true -> c = true. Proof. intros [] []. (*bc相等的情况不需要再进行筛选*) -reflexivity. (*bs不相等的情况则需要进行筛选*) -simpl. intro H. rewrite H. reflexivity. -reflexivity. -simpl. intro H. rewrite H. reflexivity. Qed.
需要注意的是这里所使用的关键字[simpl],正如前面所介绍的一样,[simpl]用于简化等式的两边,但是由于[reflexivity]自带简化的功能,所以通常都不会使用[simpl]关键字;然而虽然[reflexivity]自带简化的功能,但执行[reflexivity]的时候也会自动验证推论,如果无法匹配则无法执行;所以[simpl]的用处就体现在这个地方:可以在验证推论之前来简化等式的两边。
除了上面讨论的情况,还有一种关于函数的推论,证明这种类型的推论,只有有正确的变量引入顺序,将普遍的量词改写为对应的变量即可:
Theorem identity_fn_applied_twice: forall (f: bool -> bool), (forall (x: bool), f x = negb x) -> forall (b: bool), f (f b) = b. Proof. intros f. (*f : bool -> bool*) intros H. (*H : forall x : bool, f x = negb x*) intros x. (*x : bool*) rewrite H. (*rewrite f for the first time*) destruct x. -rewrite H(*rewrite f second time*). reflexivity. -rewrite H. reflexivity. Qed.
同一个推论可能会有不一样的证明方法,但最终的目的都是证明这个推论成立;在实际的证明过程中,如何证明推论需要看证明过程的状态显示,在正确的地方使用正确的关键字从而达到目的。