pygal 是非常不错的 python 可视化包,它可以生成矢量图,从而在不同尺寸的屏幕上都可以获得良好的显示效果。具体安装使用请参考官方文档。今天小狼举个投骰子的栗子,看一下不同点数的概率分布情况。源码请移步小狼 GitHub 下的 roll_dice_pygal 文件夹。
最常见的骰子是 6 个面的,点数分别从 1 至 6, 玩法上可以只投一个骰子,同时投两个骰子或者更多,在这里我们分别计算投一个,投两个和投三个的情况。
1. 投一个骰子的点数分布
每次投掷骰子的点数可以用 random 中的 randint 来实现,然后写两个函数方便待会儿复用:roll_dice() 用来模拟每次投掷骰子的点数,frequencies() 用来计算每个点数的频率。
from random import randint
def roll_dice():
results = []
for num in range(times):
result = randint(1, sides)
results.append(result)
return results
def frequencies(x):
results = []
for num in range(1, sides+1):
result = x.count(num)
results.append(result)
return results
设置骰子的面数为 6,投掷次数为 100 次:
sides = 6
times = 100
存储投掷结果(不放心的话可以 print 出来检查一下代码),计算每个点数的频率,把频率打印出来:
roll_results = roll_dice()
frequencies = frequencies(roll_results)
print(frequencies)
运行一下代码,得到频率的结果:
[17, 19, 15, 16, 13, 20]
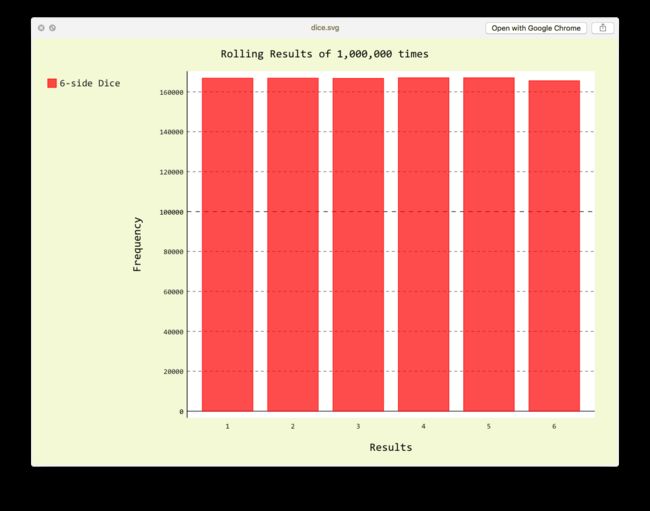
上面的列表返回的分别是骰子 1 - 6 的频率结果,例如投掷 100 次,点数为 1 的次数共计是 17 次。看上去没什么问题,是时候该 pygal 上场了!
import pygal
freq_visual = pygal.Bar()
我们导入了 pygal,然后决定用柱状图来显示结果。接下来我们顺便对即将显示的图表做一些优化,让它更易读:
freq_visual.title = 'Rolling Results of 100 times'
freq_visual.x_labels = [str(x) for x in range(1, 7)]
freq_visual.x_title = 'Results'
freq_visual.y_title = 'Frequency'
接下来导入参数并且绘制图表:
freq_visual.add('6-side Dice', frequencies)
freq_visual.render_to_file('dice.svg')
我们得到了一个 .svg 格式的图,可以用浏览器打开查看,该格式也可以用 Adobe Illustrator 打开编辑。
你和朋友玩了 100 次,你朋友赌 6 赢了 20 次,你赌 5 赢了 13 次,乍看下去似乎不是等概率事件?其实是因为投掷的次数太少了!你再和他玩个一万次,一百万次看看:
呵呵,呵呵呵。
2. 两个骰子的点数分布
现在我们同时投掷两个骰子,每次的结果等于两个骰子点数之和,稍稍修改一下计算频率的函数:
def frequencies(x):
results = []
for num in range(2, sides*2+1):
result = x.count(num)
results.append(result)
return results
把第二个骰子的点数纳入到结果中:
roll_results_1 = roll_dice()
roll_results_2 = roll_dice()
roll_results = [roll_results_1[i]+roll_results_2[i] for i in range(times)]
记得改一下 x 轴坐标:
freq_visual.x_labels = [str(x) for x in range(2, 13)]
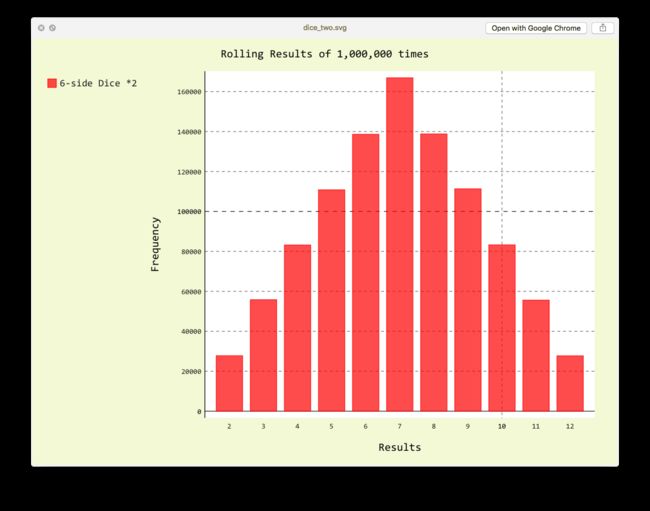
来看看模拟投掷 100 次,10,000 次和 1,000,000 次的结果:
额,看来还是赌 7 是王道,但是前 100 次的输赢就看你的人品了。。。
3. 三个骰子的点数分布
现在我们同时投掷三个骰子,每次的结果等于三个骰子点数之和,再稍稍修改一下计算频率的函数:
def frequencies(x):
results = []
for num in range(3, sides*3+1):
result = x.count(num)
results.append(result)
return results
把第三个骰子的点数纳入到结果中:
roll_results_1 = roll_dice()
roll_results_2 = roll_dice()
roll_results_3 = roll_dice()
roll_results = [roll_results_1[i]+roll_results_2[i]+roll_results_3[i] for i in range(times)]
最后记得改一下 x 轴坐标:
freq_visual.x_labels = [str(x) for x in range(3, 19)]
模拟投掷 100 次,10,000 次和 1,000,000 次的结果:
总之,相信你赌 10 和 11 在多数情况下都是能够完胜你那个赌 1 和 18 的朋友的。不过,小赌怡情,大赌伤身哦!