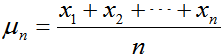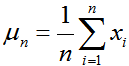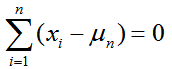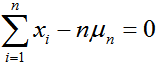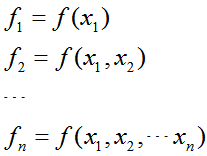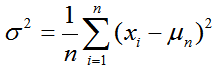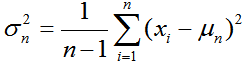基于.Net Core 2.0的平均值和样本方差的递推算法
1.平均值的递推算法
1.1 定义
设有一组数
其平均值定义为
也可以记为
由上述定义可以得出一个推论,如下所示:
推论1下述表达式成立
证明:由(1)可得
从而有
于是(3)成立。
1.2 代码实现
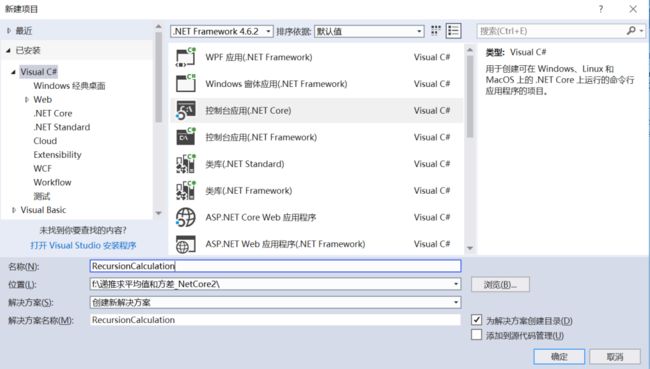
打开Visual Studio 2017,点击“文件”→“新建”→“项目”,选择控制台应用(.NET Core),如下所示:
新建一个文件,命名为RecursionCalculator.cs,在自动生成的类RecursionCalculator里面添加方法,如下所示:
代码1 递推计算类RecursionCalculator和平均值计算方法Average0
using System;
using System.Collections.Generic;
namespace RecursionCalculation
{
public class RecursionCalculator
{
public static double Average0(IList data)
{
if(data == null)
{
throw new ArgumentNullException(nameof(data), "不能是空对象");
}
if(data.Count == 0)
{
return 0;
}
double sum = data[0];
for(int i = 1; i < data.Count; i++)
{
sum += data[i];
}
return sum / data.Count;
}
}
}
在启动文件Program.cs中在类Program中添加测试方法,如下所示:
代码2 使用随机数测试平均值计算方法RecursionCalculator.Average0
using System;
using System.Collections.Generic;
namespace RecursionCalculation
{
class Program
{
static void Main(string[] args)
{
Test_Average0();
}
static void Test_Average0()
{
//定义初始容量
int capacity = 10;
//定义初始容量为capacity的int列表
List data = new List(capacity);
//采用当前时刻作为随机种子,定义一个随机数发生器
Random rand = new Random((int)DateTime.Now.Ticks);
//随机生成capacity个数字,加入列表
for (int i = 0; i < capacity; i++)
{
data.Add(rand.Next(85, 100 + 1)); //添加一个[85, 100]之间的随机数
}
//求平均值
double average = RecursionCalculator.Average0(data);
//输出
Console.Write($"{capacity}个随机数为:");
for(int i = 0; i < capacity; i++)
{
Console.Write(data[i]);
Console.Write(" ");
}
Console.WriteLine();
Console.WriteLine("平均值=" + average.ToString());
}
}
}
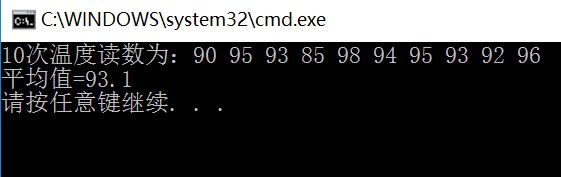
输出如下:
需要注意的是,读者的电脑中可能产生不同的输出结果。
1.3 平均值的递推计算
1.3.1 一个模拟实例——锅炉温度平均值
假设我们正在监控锅炉的温度,需要根据一段时间内的平均温度采取某种控制措施。使用温度传感器采集温度,采集周期假设1秒钟一次。现在,假设已经采集了个温度值,用来表示,则其平均温度可以用式(2)算出,具体程序代码如代码1所示。
由式(2)可知,要计算的平均值,需要对个值进行累加,计算机需要扫描个数,执行次加法操作和1次除法操作。
为了方便说明问题,我们新建一个类TemperatureCollector,模拟一个锅炉的温度采集器,并假设温度范围为[85, 100]。新建文件TemperatureCollector.cs,为类TemperatureCollector添加温度采集方法,如下所示:
代码3 温度采集器TemperatureCollector
using System;
namespace RecursionCalculation
{
public class TemperatureCollector
{
private Random _rand = new Random((int)DateTime.Now.Ticks);
public TemperatureCollector()
{
}
//采集温度
public int Collect0()
{
return _rand.Next(85, 100 + 1); //模拟一个[85, 100]之间的温度读数
}
}
}
现在,文件Program.cs中的测试方法应该改为如下所示:
代码4 计算平均温度
static void Test_Average0()
{
//定义初始容量
int capacity = 10;
//定义温度采集器
TemperatureCollector collector = new TemperatureCollector();
//定义初始容量为capacity的int列表
List data = new List(capacity);
//随机生成capacity个数字,加入列表
for (int i = 0; i < capacity; i++)
{
data.Add(collector.Collect0());
}
//求平均值
double average = RecursionCalculator.Average0(data);
//输出
Console.Write($"{capacity}次温度读数为:");
for(int i = 0; i < capacity; i++)
{
Console.Write(data[i]);
Console.Write(" ");
}
Console.WriteLine();
Console.WriteLine("平均值=" + average.ToString());
}
在新的采集周期里,我们获得了最新的温度值,仍然按照式(2)来计算平均值,如下所示:
如果仍然用代码4来演示,则只需修改语句int capacity = 10;为int capacity = 11;,显然,这种做法毫无乐趣,也不符合实际情况。其原因在于,我们未将数据与对象的关系处理好。现在修正一下,将温度数据保存到温度采集器里,且将温度值的数据类型改为double,以便更符合实际情况。
1)改动1:让递推计算类接受double类型的列表,改后的代码如下所示:
public class RecursionCalculator
{
public static double Average0(IList<double> data)
{
…… //其他内容不变
}
}
2)改动2:将采集到的温度值放在类TemperatureCollector的对象里,改后的代码如下所示:
using System;
using System.Collections.Generic;
using System.Threading;
namespace RecursionCalculation
{
public class TemperatureCollector
{
//随机数发生器,模拟一个温度传感器
private Random _rand = new Random((int)DateTime.Now.Ticks);
//温度值列表
private List _data = new List();
//是否正在采集数据,true - 是,false - 否
private bool _working = false;
//采集周期
private int _cycle = 1000;
//采集线程
private Thread _thread = null;
public TemperatureCollector(int cycle = 1000)
{
if(cycle < 0)
{
cycle = 0; //真实环境中应该抛出异常
}
if(cycle > 10000)
{
cycle = 10000; //真实环境中应该抛出异常
}
_cycle = cycle;
}
//开始采集
public void Start()
{
Console.WriteLine("主线程号:" + Thread.CurrentThread.ManagedThreadId.ToString());
if(_working)
{
_working = false;
_thread.Join();
_thread = null;
}
_working = true;
_data.Clear();
_thread = new Thread(new ThreadStart(collect));
_thread.Start();
}
//停止采集
public void Stop()
{
if(_working)
{
_working = false;
_thread.Join();
_thread = null;
}
}
//清空当前存储的数据
public void Clear()
{
_data.Clear();
}
//获得当前平均温度值
public double Average()
{
double avg = RecursionCalculator.Average0(_data);
return avg;
}
//循环采集温度
private void collect0()
{
Console.WriteLine("采集线程号collect0():" + Thread.CurrentThread.ManagedThreadId.ToString());
while (_working)
{
_data.Add(_rand.Next(85, 101));
Thread.Sleep(_cycle);
}
}
}
}
3)改动3:在Program.cs中修改测试方法,改动后的代码如下:
using System;
using System.Threading;
namespace RecursionCalculation
{
class Program
{
static void Main(string[] args)
{
Test_TemperatureCollector_Average();
}
static void Test_TemperatureCollector_Average()
{
int count = 10; //查看平均值的次数
int cycle = 500; //采集周期(毫秒)
TemperatureCollector collector = new TemperatureCollector(cycle);
collector.Start();
for(int i = 0; i < count; i++)
{
Console.WriteLine($"最新平均温度 = {collector.Average().ToString("F2")}");
Thread.Sleep(cycle);
}
collector.Stop();
}
}
}
1.3.2 平均值递推计算的必要性
在小节1.3.1中,我们查看了10次平均值,每次查看平均值时,都要调用方法TemperatureCollector.Average(),在该方法里调用方法RecursionCalculator.Average0(_data)进行平均值计算。每次计算平均值时,都要将当前所有已采集到的温度值全都累加一遍。
可以想象一下,我们要实时显示当前平均温度,将温度采集周期设为100毫秒,从凌晨0:00开始采集,到10:00点时,已经采集到10×60×60×10= 360000个读数。在下一个采集值到达后,求新的平均值时,需要累加360001个温度值,这将非常耗时。当温度值个数达到某一个临界点时,求平均值所花的时长将大于采集周期,从而严重影响实时性。
当代计算机运行速度很快,360001个数据的平均值或许不算什么,但当数据个数达到上亿的时候,问题就非常明显了。
读者们想必已经知道,我们上述计算平均值的算法RecursionCalculator.Average0(_data),其时间复杂度为O(n),即为线性复杂度。对计算温度平均值而言,线性复杂度是不可忍受的,必须降低复杂度。比线性复杂度还低的复杂度,有对数复杂度log2(n)和常数复杂度O(1)。本文的目标之一,就是实现常数复杂度的平均值计算算法。
具体怎么做呢?在计算数学里面,有一种算法,叫做递推算法。简单解释如下:设f(比如温度平均值)是变量x(比如温度)的函数,变量在不同的时刻t有不同的取值,f在每个时刻的值皆与已经出现过的所有x值有关系,即
��
递推算法的大概含义是指,若要求得第n+1个函数值f_(n+1),只需要知道f_n和x_(n+1)即可,无需知道更早的数据x1,x2,……,x_n和f1,f2,……,f_(n-1)。当然,实际的递推算法,有可能涉及到比f_n和x_(n+1)更早的少数几个数据,例如x_n和f_(n-1),但这些依赖数据的具体个数是有限的,而不是随着时间的增加而增加。
在算法RecursionCalculator.Average0(_data)中,每次计算平均值时,都要依赖最新的数据和所有更早的数据,因此它不是递推算法。
1.3.3 平均值递推计算算法
由式(2)可知,
也即:
这就是平均值的递推计算公式。
现在,我们使用式(9)设计新的C#代码。由式(9)可知,新的平均值仅与上次平均值、已有数据个数、最新数据有关系,也就是说新的平均值方法要有三个参数。代码如下所示:
代码5 平均值递推算法RecursionCalculator.AverageRecursively
public static double AverageRecursively(double newestValue, int existedCount, double lastAverage)
{
if(existedCount < 1)
{
return newestValue;
}
double avg = lastAverage + (newestValue - lastAverage) / (existedCount + 1);
return avg;
}
代码6修改后的温度采集器类TemperatureCollector
……//内容不变
namespace RecursionCalculation
{
public class TemperatureCollector
{
……//内容不变
//上次平均值
private double _lastAverage = 0;
……
//开始采集
public void Start(int methodType = 0)
{
……
if(methodType == 0)
{
_thread = new Thread(new ThreadStart(collect0));
}
else
{
_thread = new Thread(new ThreadStart(collectRecursively));
}
……
}
……
//清空当前存储的数据
public void Clear()
{
_lastAverage = 0;
_data.Clear();
}
……
public double AverageRecursively()
{
return _lastAverage;
}
//循环采集温度
private void collectRecursively()
{
Console.WriteLine("采集线程号collectRecursively():" + Thread.CurrentThread.ManagedThreadId.ToString());
double newestValue = 0;
int existedCount = 0;
while (_working)
{
newestValue = _rand.Next(85, 101);
_data.Add(newestValue); //如果无需保存历史采集数据,则可以去掉该语句,以节省空间
_lastAverage = RecursionCalculator.AverageRecursively(newestValue, existedCount, _lastAverage);
existedCount++;
Thread.Sleep(_cycle);
}
}
}
}
测试方法如下:
……
static void Main(string[] args)
{
//Test_TemperatureCollector_Average();
Test_TemperatureCollector_AverageRecursively();
}
static void Test_TemperatureCollector_AverageRecursively()
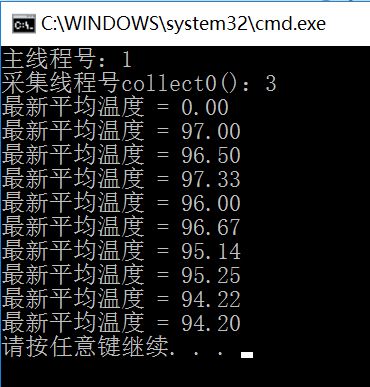
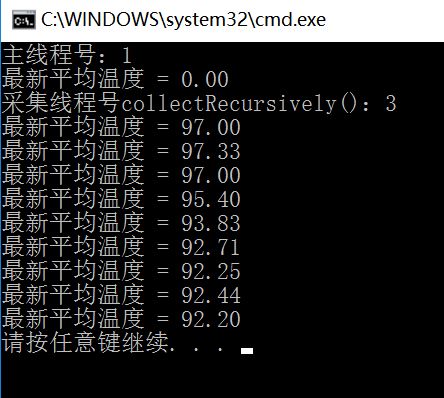
{
int count = 10; //查看平均值的次数
int cycle = 500; //采集周期(毫秒)
TemperatureCollector collector = new TemperatureCollector(cycle);
collector.Start(1);
for (int i = 0; i < count; i++)
{
Console.WriteLine($"最新平均温度 = {collector.AverageRecursively().ToString("F2")}");
Thread.Sleep(cycle);
}
}
1.2.4 性能比较
(一)理论分析
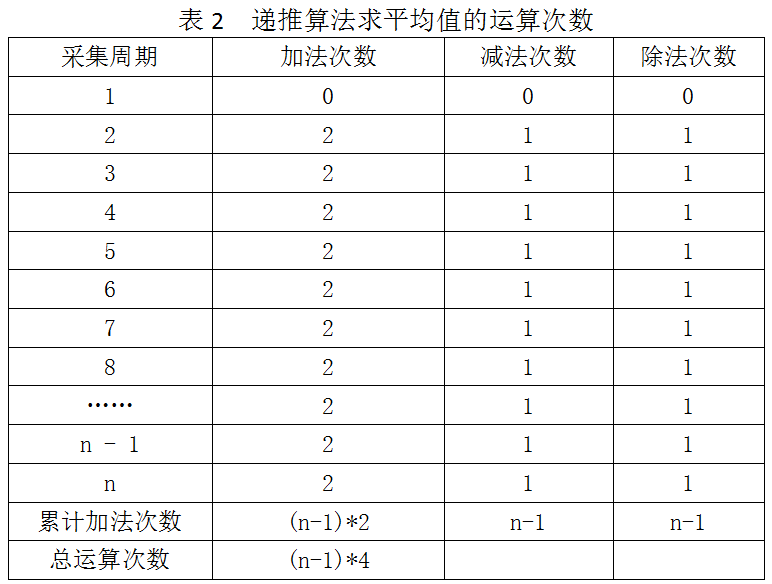
线性算法求平均值使用的公式是式(2),每求一次平均值,需要执行n-1次加法和1次除法(假设相当于1次加法)。若要在温度循环采集过程中实时显示平均温度,则第n次温度采集后计算平均值需要n-1次加法,列表如下:
递推算法求平均值使用的是公式(9),每求一次平均值,需要执行2次加法,1次减法(假设相当于1次加法)和1次除法(假设相当于1次加法),列表如下:
由此可见,使用线性算法实时求取平均值的时间复杂度是O(n2),而递推算法的时间复杂度是O(n)。
(二)实际测试
在这里,我们将对线性算法和递推算法求平均值的性能进行实际测试,为此,需要做以下几点改动:
(1)为了避免无关因素的干扰,将避开类TemperatureCollector,而直接调用类RecursionCalculator的相关方法。
(2)为了保证两种算法使用的是同一种数据,我们在每次求平均值之前,生成一份随机数据,该份数据同时用于线性算法和递推算法。
相关代码改动如下:
1)为类RecursionCalculator增加新的方法,如下所示:
//求data列表中前count个数据的平均值
public static double Average0_static(IList data, int count)
{
if (data == null)
{
throw new ArgumentNullException(nameof(data), "不能是空对象");
}
if (data.Count == 0)
{
return 0;
}
double sum = data[0];
for (int i = 1; i < Math.Min(data.Count, count); i++)
{
sum += data[i];
}
return sum / data.Count;
}
2)在Program.cs文件中,为类Program增加两个字段和两个方法:
static Dictionary linearElapsedTime = null;
static Dictionary recursiveElapsedTime = null;
static void Test_TemperatureCollector_AverageAndAverageRecursively_Performance()
{
int interval = 2000;
int testCount = 18;
linearElapsedTime = new Dictionary(testCount);
recursiveElapsedTime = new Dictionary(testCount);
for (int i = 1; i <= testCount; i++)
{
Test_TemperatureCollector_AverageAndAverageRecursively(interval * i);
}
string filePath = @"D:\test.txt";
StreamWriter file = File.CreateText(filePath);
string s = "";
file.WriteLine("线性算法求平均值所耗时间:求值次数 时间(毫秒)");
foreach (int capacity in linearElapsedTime.Keys)
{
s = "";
s = capacity.ToString() + " " + linearElapsedTime[capacity].ToString();
file.WriteLine(s);
}
file.WriteLine();
file.WriteLine();
file.WriteLine("递推算法求平均值所耗时间:求值次数 时间(毫秒)");
foreach (int capacity in recursiveElapsedTime.Keys)
{
s = "";
s = capacity.ToString() + " " + recursiveElapsedTime[capacity].ToString();
file.WriteLine(s);
}
file.Close();
}
static void Test_TemperatureCollector_AverageAndAverageRecursively(int capacity)
{
Stopwatch w = new Stopwatch();
List data = new List(capacity);
Random rand = new Random((int)DateTime.Now.Ticks);
for(int i = 0; i < capacity; i++)
{
data.Add(rand.Next(85, 101));
}
double avg = 0;
#region 线性算法求平均值
w.Start();
for (int i = 1; i <= capacity; i++)
{
avg = RecursionCalculator.Average0_static(data, i);
}
w.Stop();
linearElapsedTime.Add(capacity, w.ElapsedMilliseconds);
#endregion
#region 递推算法求平均值
avg = 0;
w.Restart();
for (int i = 0; i < capacity; i++)
{
avg = RecursionCalculator.AverageRecursively(data[i], i, avg);
}
w.Stop();
recursiveElapsedTime.Add(capacity, w.ElapsedMilliseconds);
#endregion
}
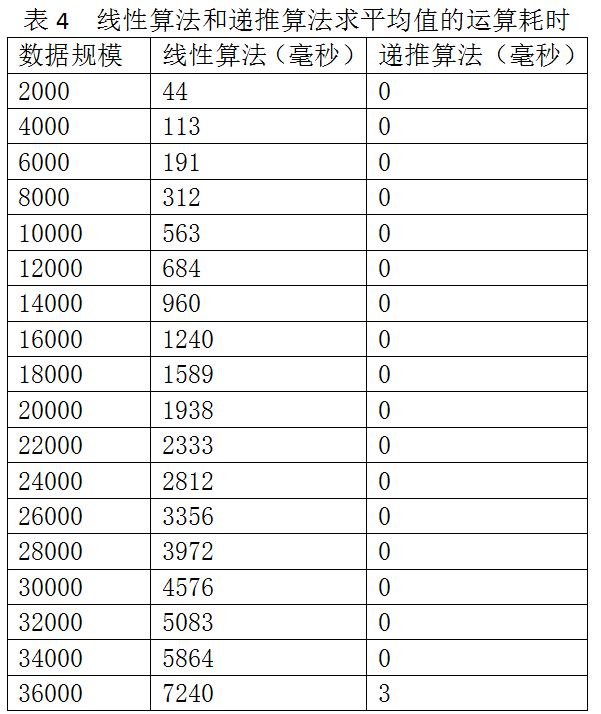
最终输出的文件内容,如下表所示:
1.4结论
可见,基于递推算法的平均值计算,其性能要比普通的线性算法好的多。
[if !supportLists]2. [endif]样本方差的递推算法
2.1 定义
设有一组数,其总体方差定义为
其中为σ^2总体方差,n为总体例数。由定义可见,σ^2描述了一组数据与均值之间的偏离程度,σ^2越大,说明这组数据的越不一致。不过,由于σ^2取的是平方,而样本值x和均值μ皆为一次方,二者不方便比较,因此通常对σ^2开平方,其结果σ称为总体标准差。
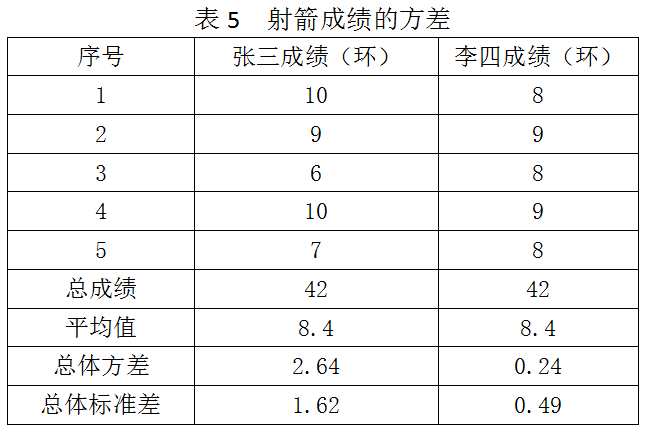
举个例子,张三和李四均为射箭运动员,他们分别射出5箭,成绩如下:
由上表可以看出,两人的平均成绩一致,难分伯仲,但张三的总体标准差为1.62,李四的则为0.49,显然李四的成绩更为稳定。通俗地说,每次射箭前,可以预测张三所得的环数与平均值差别大概在1.62环,而李四则为0.49环,可见,李四的发挥更为稳定,而张三发挥的波动较大。
在现实中,通常很难获得某个统计指标的全部数据,例如,很难获得世界上每一个人的身高,只能获取部分样本的数据,例如只能抽查获得少数个体的身高,因此,就改用样本方差和样本标准差来计算,定义如下:
当n=1时,定义σ^2的值为0。
2.2 样本方差的递推计算
2.2.1 公式推导
由式(11)可知
最终结果为
由式(13)可知,第个样本方差只与上次方差σ^2_n、已有样本数n、上次均值μ_n、最新数据x_(n+1)和最新均值μ_(n+1)有关,而由式(9)可知,新的平均值μ_(n+1)仅与上次平均值μ_n、已有样本数n、最新数据x_(n+1)有关系,因此,最新的样本方差与历史数据没有关系,它只与上次方差σ^2_n、已有样本数n、上次均值μ_n和最新数据x_(n+1)有关系。
2.2.2 代码实现
1)在文件RecursionCalculator.cs中为类RecursionCalculator新增两个方法,如下所示:
//线性算法计算样本方差
public static double Variance0(IList data)
{
double variance = 0;
if (data == null)
{
throw new ArgumentNullException(nameof(data), "不能是空对象");
}
if (data.Count < 2)
{
return 0;
}
double avg = Average0(data);
double sum = 0;
for(int i = 0; i < data.Count; i++)
{
sum += (data[i] - avg) * (data[i] - avg);
}
variance = sum / (data.Count - 1);
return variance;
}
//递推算法计算样本方差
public static double VarianceRecursively(double newestValue, int existedCount, double lastAverage, double lastVariance, double newestAverage)
{
if(existedCount < 2)
{
return 0;
}
double variance = 0;
double tmp = (newestValue - lastAverage) / (existedCount + 1);
variance = (existedCount - 1) * lastVariance / existedCount + tmp * tmp + (newestValue - newestAverage) / existedCount;
return variance;
}
2)在TemperatureCollector.cs中为类TemperatureCollector新增字段,如下所示:
//上次样本方差
private double _lastVariance = 0;
3)在TemperatureCollector.cs中为类TemperatureCollector在方法public void Start(int methodType = 0)中的语句_lastAverage = 0;后面添加如下代码:
_lastVariance = 0;
4)在TemperatureCollector.cs中为类TemperatureCollector增加两个方法:
//线性算法计算温度数据集的样本方差
public double Variance0()
{
double variance = RecursionCalculator.Variance0(_data);
return variance;
}
//递推算法计算温度数据集的样本方差
public double VarianceRecursively()
{
return _lastVariance;
}
4)在TemperatureCollector.cs中为类TemperatureCollector修改方法private void collectRecursively(),改后如下所示:
private void collectRecursively()
{
Console.WriteLine("采集线程号collectRecursively():" + Thread.CurrentThread.ManagedThreadId.ToString());
double newestValue = 0;
int existedCount = 0;
double tmp = 0;
while (_working)
{
newestValue = _rand.Next(85, 101);
_data.Add(newestValue); //如果无需保存历史采集数据,则可以去掉该语句,以节省空间
tmp = _lastAverage;
_lastAverage = RecursionCalculator.AverageRecursively(newestValue, existedCount, _tmp );
_lastVariance = RecursionCalculator.VarianceRecursively(newestValue, existedCount, tmp, _lastVariance, _lastAverage);
existedCount++;
Thread.Sleep(_cycle);
}
}
5)在文件Program.cs中为类Program增加方法,如下所示:
static void Test_TemperatureCollector_VarianceAndVarianceRecursively()
{
int count = 10; //查看样本方差的次数
int cycle = 500; //采集周期(毫秒)
TemperatureCollector collector = new TemperatureCollector(cycle);
#region 使用线性算法计算样本方差
collector.Start(0);
for (int i = 0; i < count; i++)
{
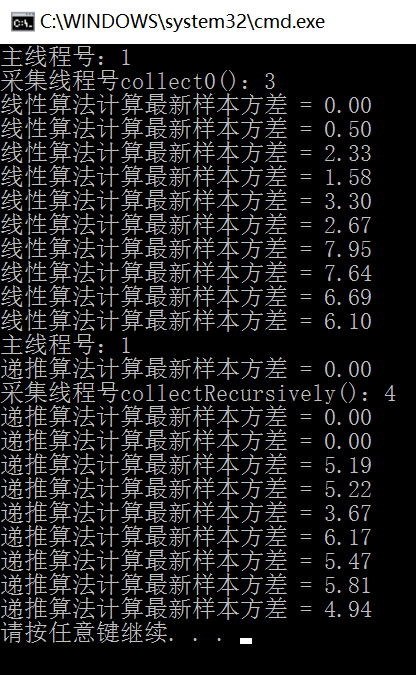
Console.WriteLine($"线性算法计算最新样本方差 = {collector.Variance0().ToString("F2")}");
Thread.Sleep(cycle);
}
collector.Stop();
#endregion
#region 使用递推算法计算样本方差
collector = new TemperatureCollector(cycle);
collector.Start(1);
for (int i = 0; i < count; i++)
{
Console.WriteLine($"递推算法计算最新样本方差 = {collector.VarianceRecursively().ToString("F2")}");
Thread.Sleep(cycle);
}
collector.Stop();
#endregion
}
6)在文件Program.cs中为类Program修改方法static void Main(string[] args),改后如下所示
//Test_TemperatureCollector_Average();
//Test_TemperatureCollector_AverageRecursively();
//Test_TemperatureCollector_AverageAndAverageRecursively_Performance();
Test_TemperatureCollector_VarianceAndVarianceRecursively();
输出结果如下:
3. 结论
本文讨论了平均值和样本方差的递推算法实现,论证其效果比线性算法好很多,并给出了基于.Net Core 2.0的C#实现。
由于本人学识有限,文中内容可能存在不少错误,请指正。