转自https://www.cnblogs.com/arxive/p/6017260.html
一、基本概念
首先简单介绍一下地理坐标系、大地坐标系以及地图投影的概念:
地理坐标系:为球面坐标。 参考平面地是椭球面,坐标单位:经纬度;
投影坐标系:为平面坐标。参考平面地是水平面,坐标单位:米、千米等;
地理坐标转换到投影坐标的过程可理解为投影。(投影:将不规则的地球曲面转换为平面)
从以上三个概念相应到可以涉及到三个问题:
地理坐标系的定义,即参考椭球面的标准,地球是一个不规则的球形,因此若用经纬度去定义地球上的位置,一定会对地球做了相应的抽象。
投影坐标系的定义,在小范围内可以认为大地是平面的,而整体上来说地球是球形的,因此大地坐标对于不同的地区肯定是不一样的。一个坐标系肯定会涉及到坐标原点、坐标轴的位置,这也是大地坐标系需要考虑的问题。
从地理坐标到投影坐标是将不规则的球面展开为平面的过程,因此也是一个将曲面拉平的过程。从生活经验中可以看出这是一个无法精确处理的问题(例如,在剥桔子的时候,如果不破坏橘子皮是无法从原来的“曲面”展开为平面的),这边涉及到了投影方法的问题
针对上面三个问题,本文将一一介绍。
二、对不规则的抽象——地球空间模型
地球的自然表面是崎岖不平的,在地理课本上我们会看到对地球形状的描述:地球是一个两极稍扁,赤道略鼓的不规则球体。
不难看出在地球的自然状态下其表面并不是连续不断的,高山、悬崖的存在,使得地球表面存在无数的凸起和凹陷,因此,对地球表面的第一层抽象,大地水准面即得到了一个连续、闭合的地球表面。大地水准面的定义是:假设当海水处于完全静止的平衡状态时,从海平面延伸到所有大陆下部,而与地球重力方向处处正交的一个连续、闭合的曲面,这就是大地水准面。它是重力等位面。
在大地水准面的基础上可以建立地球椭球模型。大地水准面虽然十分复杂,但从整体来看,起伏是微小的,且形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体,这个椭球体称为地球椭球体。其表面是一个规则数学表面,可用数学公式表达,所以在测量和制图中用它替代地球的自然表面。地球形体的二级逼近。
地球椭球体有3个参数,长半轴,短半轴和扁率。可以想象地球椭球体就是一个没有那么扁长的橄榄球的形状。
三、地理坐标系(大地坐标系)
有了对地球的抽象——参考椭球体就可以建立地理坐标系了,但是这里存在一个问题,参考椭球体是对地球的抽象,因此其并不能去地球表面完全重合,在设置参考椭球体的时候必然会出现有的地方贴近的好(参考椭球体与地球表面位置接近),有地地方贴近的不好的问题,因此这里还需要一个大地基准面来控制参考椭球和地球的相对位置。
有以下两类基准面:
地心基准面:由卫星数据得到,使用地球的质心作为原点,使用最广泛的是 WGS 1984。
区域基准面:特定区域内与地球表面吻合,大地原点是参考椭球与大地水准面相切的点,例如Beijing54、Xian80。
每个国家或地区均有各自的大地基准面。我们通常称谓的Beijing54、Xian80坐标系实际上指的是我国的两个大地基准面。相对同一地理位置,不同的大地基准面,它们的经纬度坐标是有差异的。
椭球体与大地基准面之间的关系是一对多的关系。因为基准面是在椭球体的基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面。
在目前的GIS商用软件中,大地基准面都通过当地基准面向WGS84的转换7参数来定义,即:
三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值。
三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角。
最后是比例校正因子,用于调整椭球大小。
Beijing54、Xian80相对WGS84的转换参数至今也没有公开,实际工作中可利用工作区内已知的北京54或西安80坐标控制点进行与WGS84坐标值的转换,在只有一个已知控制点的情况下(往往如此),用已知点的北京54与WGS84坐标之差作为平移参数,当工作区范围不大时,如青岛市(10654平方公里),精度也足够了。
有了参考椭球和大地基准面两个因素就可以建立地理坐标系了。地理坐标系(大地坐标系)是大地测量中以参考椭球面为基准面建立起来的坐标系。地面点的位置用经度、纬度、和大地高度表示。地理坐标系在GIS软件中的定义如下所示:
Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian(起始经度): Greenwich (0.000000000000000000)
Datum(大地基准面): D_Beijing_1954
Spheroid(参考椭球体): Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000
大地坐标系可分为参心大地坐标系和地心大地坐标系。
参心大地坐标系:指经过定位与定向后,地球椭球的中心不与地球质心重合而是接近地球质心。区域性大地坐标系。是我国基本测图和常规大地测量的基础。如Beijing54、Xian80。
地心大地坐标系:指经过定位与定向后,地球椭球的中心与地球质心重合。如CGCS2000、WGS84。
因此参心大地坐标系和地心大地坐标系的区别也就在于大地基准面的选择了。
到这里我们已经介绍了地理坐标系上经纬度的来源了,还需要考虑的是高程信息的标准化。
高程控制网的建立,必须规定一个统一的高程基准面。我国利用青岛验潮站1950~1956年的观测记录,确定黄海平均海水面为全国统一的高程基准面,并在青岛观象山埋设了永久性的水准原点。以黄海平均海水面建立起来的高程控制系统,统称“1956年黄海高程系”。
1987年,因多年观测资料显示,黄海平均海平面发生了微小的变化,由原来的72.289m变为72.260m,国家决定启用新的高程基准面,即“1985年国家高程基准”。高程控制点的高程也发生微小的变化,但对已成图上的等高线的影响则可忽略不计。
国家高程控制网是确定地貌地物海拔高程的坐标系统。按控制等级和施测精度分为一、二、三、四等网。目前提供使用的1985国家高程系统共有水准点成果114041个,水准路线长度为416619.1公里。
四、曲面变平面——投影的作用
将地球椭球面上的点映射到平面上的方法,称为地图投影。
为什么要进行投影?
地理坐标为球面坐标,不方便进行距离、方位、面积等参数的量算。
地球椭球体为不可展曲面。
地图为平面,符合视觉心理,并易于进行距离、方位、面积等量算和各种空间分析。
地球椭球表面是一种不可能展开的曲面,要把这样一个曲面表现到平面上,就会发生裂隙或褶皱。在投影面上,可运用经纬线的“拉伸”或“压缩”(通过数学手段)来加以避免,以便形成一幅完整的地图。但不可避免会产生变形。
地图投影的变形通常有:长度变形、面积变形和角度变形。在实际应用中,根据使用地图的目的,限定某种变形。
按变形性质分类:
等角投影:角度变形为零(Mercator)
等积投影:面积变形为零(Albers)
任意投影:长度、角度和面积都存在变形
其中,各种变形相互联系相互影响:等积与等角互斥,等积投影角度变形大,等角投影面积变形大。
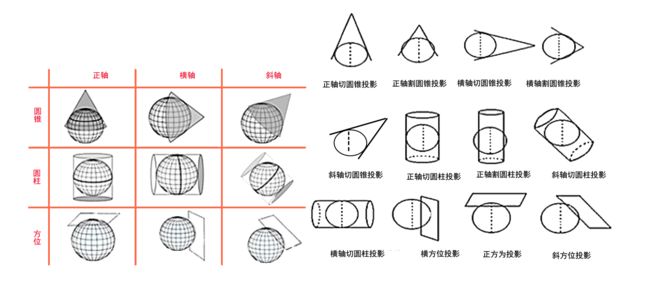
从投影面类型划分:
横圆柱投影:投影面为横圆柱
圆锥投影:投影面为圆锥
方位投影:投影面为平面
从投影面与地球位置关系划分为:
正轴投影:投影面中心轴与地轴相互重合
斜轴投影:投影面中心轴与地轴斜向相交
横轴投影:投影面中心轴与地轴相互垂直
相切投影:投影面与椭球体相切
相割投影:投影面与椭球体相割
选择地图投影时,主要考虑因素
制图区域的范围、形状和地理位置(主要因素)
地图的用途、出版方式及其他特殊要求
投影选择实例
世界地图,主要采用正圆柱、伪圆柱和多圆锥投影。在编绘世界航线图、世界交通图与世界时区图时也采用墨卡托投影。
中国出版的世界地图多采用等差分纬线多圆锥投影 。
对于半球地图,东、西半球图常选用横轴方位投影;南、北半球图常选用正轴方位投影;水、陆半球图一般选用斜轴方位投影。
在东西延伸的中纬度地区,一般采用正轴圆锥投影,如中国与美国。
在南北方向延伸的地区,一般采用横轴圆柱投影或多圆锥投影,如智利与阿根廷 。
投影参数:
标准线
概念:投影面与参考椭球的切线或割线。分为标准纬线与标准经线。
特点:没有变形,也称主比例尺。
中心线
概念:是指中央经线(原点经线)与中央纬线(原点纬线),用来定义图投影的中心或者原点。
特点:一般会有变形。
我国常用的投影方式
我国基本比例尺地形图(1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000)除1:100万以外均采用高斯-克吕格Gauss-Kruger投影(横轴等角切圆柱投影,又叫横轴墨卡托Transverse Mercator投影)为地理基础。
1:100万地形图采用兰伯特Lambert投影(正轴等角割圆锥投影),其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影保持一致。
海上小于50万的地形图多用墨卡托Mercator投影(正轴等角圆柱投影)。
我国大部份省区图以及大多数这一比例尺的地图也多采用Lambert投影和属于同一投影系统的Albers投影(正轴等积割圆锥投影)。
五、高斯-克吕格Gauss-Kruger投影(横轴等角切圆柱投影)
我国规定1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万比例尺的地形图均采用高斯克吕格投影。该投影在英美等国家被称为横轴墨卡托投影
横轴等角切圆柱投影
– 离开中央子午线越远,变形越大
– 赤道是直线,离开赤道的纬线是弧线,凸向赤道
– 没有角度变形
– 长度和面积变形很小
北京54和西安80投影坐标系的投影方式
高斯投影特点:
– 中央子午线长度变形比为1
– 在同一条经线上,长度变形随纬度的降低而增大,在赤道处为最大
– 在同一条纬线上,长度变形随经差的增加而增大,且增大速度较快
– 在6˚带范围内,长度最大变形不超过0.14%
通过分带控制变形:
– 6°分带: 用于1:2.5万 ~1:50万比例尺地图
起始于初子午线(格林威治),按经差6度为一个投影带自西向东划分,全球共分60个投影带。我国范围可分成11个6度带。
– 3°分带:用于大于1:1万比例尺地图
始于东经1°30′,按经差3度为一个投影带自西向东划分,全球共分120个投影带。我国范围可分成22个三度带。
– 坐标系原点为每个投影带的中央经线与赤道交点
为了便于地形图的测量作业,在高斯-克吕格投影带内布置了平面直角坐标系统,具体方法是,规定中央经线为X轴,赤道为Y轴,中央经线与赤道交点为坐标原点,x值在北半球为正,南半球为负,y值在中央经线以东为正,中央经线以西为负。由于我国疆域均在北半球,x值均为正值,为了避免y值出现负值,规定各投影带的坐标纵轴均西移500km,中央经线上原横坐标值由0变为500km。为了方便带间点位的区分,可以在每个点位横坐标y值的百千米位数前加上所在带号。
六、兰伯特Lambert投影(正轴等角割圆锥投影)
适用于小于1:100万(包括1:100万)的地图。
最适用于中纬度的一种投影。它类似于Albers投影,不同之处在于其描绘形状比描绘面积更准确。
中国地图的中央经线常位于东经105度,两条标准纬线分别为北纬25度和北纬47度。各省的参数可根据地理位置和轮廓形状初步加以判定。例如甘肃省的参数为:中央经线为东经101度,两条标准纬线分别为北纬34度和41度。
投影方法:
圆锥投影通常基于两条标准纬线,从而使其成为割投影。超过标准纬线的纬度间距将增加。这是唯一常用的将两极表示为单个点的圆锥投影。
也可使用单条标准纬线和比例尺因子定义。如果比例尺因子不等于1.0,投影实际上将变成割投影。
阿伯斯Albers投影(正轴等积割圆锥投影)
也称“双标准纬线等积圆锥投影”,为阿伯斯(Albers)拟定。投影区域面积保持与实地相等。最适合于东西方向分布的大陆板块,不适合南北方向分布的大陆板块。在处理显示400万、100万的全国数据时为了保持等面积特性,经常采用Albers投影。
墨卡托Mercator投影(正轴等角圆柱投影)
由墨卡托于1569年专门为航海目的设计的。设计思想是令一个与地轴方向一致的圆柱切于或割于地球,将球面上的经纬网按等角条件投影于圆柱表面上,然后将圆柱面沿一条母线剪开展成平面。广泛应用于航海,航空的重要投影。
投影坐标系
地图投影是将地图从球面(大地基准面)转换到平面的数学变换。由此确定的坐标系一般称为投影坐标系。因此,投影坐标系需要两组参数确定,一组为大地坐标系,另一组为投影参数。
重投影
根据以上介绍,我们可以知道当考虑两幅遥感影像、矢量地图等的坐标信息时,我们需要考虑其所在的投影坐标系。若两投影坐标系不相同则需要进行重投影变换,这里可能涉及到一下几种类型的重投影变换:
不同投影方式之间的变换。即两投影坐标系具有相同的参考椭球和大地基准面,如都是北京54地理坐标系下,但是是通过不同的投影方式得到的;
不同大地基准面的变换。此时两坐标系采用了相同的参考椭球但具有不同的大地基准面,则得到的经纬度坐标是不具备比较意义的,因此需要进行重投影变换。
不同参考椭球的变换。
如果在同一个椭球基准面下的转换就是严密的转换,如果在同一个椭球体不同基准面的转换是不严密的,不同椭球体之间的转换是不严密的,这就需要用到七参数、三参数等方法。需要两个不同坐标系统下公共点坐标求得系数。例如北京54和WG4-84坐标下的同一点的经纬度或者是经过投影后的平面坐标也是不同的。那么影像投影主要分为哪些步骤呢?说白了,就三个步骤,第一,坐标转换;第二,影像的重采样,最后就是写入到新文件中。
本文简介了地理坐标系统的相关概念,只有弄清楚了这些基础知识,才能在工作学习中遇到问题时,正确的考虑是否需要对地图信息进行重投影变换。本文不涉及代码部分的介绍,后面将会作专门的博客进行相关说明。
参考资料
[1]http://blog.sina.com.cn/s/blog_7f6303470101fzcw.html
[2]http://blog.sina.com.cn/s/blog_7f6303470101fzcq.html
[3]http://blog.sina.com.cn/s/blog_7f6303470101fzch.html
[4]http://blog.sina.com.cn/s/blog_7f6303470101fzcg.html
[5]http://blog.csdn.net/arcgis_all/article/details/8216583
[6]http://blog.csdn.net/zhouxuguang236/article/details/17468171