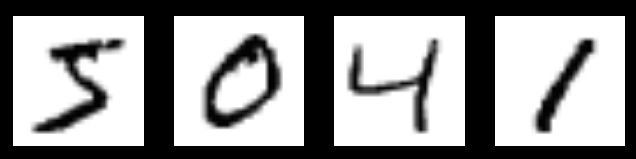MNSIT数据集
MNIST是一个入门级的计算机视觉数据集,它包含各种手写数字图片,它也包含每一张图片对应的标签,告诉我们这个是数字几。比如,下面这四张图片的标签分别是5,0,4,1。
MNIST数据集的官网是Yann LeCun's website。在这里,我们提供了一份python源代码用于自动下载和安装这个数据集。你可以下载这份代码,然后用下面的代码导入到你的项目里面,也可以直接复制粘贴到你的代码文件里面。它会在你的程序同级目录自动创建一个'MNIST_data'目录来存储数据。
import tensorflow.examples.tutorials.mnist.input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
下载下来的数据集被分成两部分:60000行的训练数据集(mnist.train)和10000行的测试数据集(mnist.test)。这样的切分很重要,在机器学习模型设计时必须有一个单独的测试数据集不用于训练而是用来评估这个模型的性能,从而更加容易把设计的模型推广到其他数据集上(泛化)。每一个MNIST数据单元有两部分组成:一张包含手写数字的图片和一个对应的标签。我们把这些图片设为“xs”,把这些标签设为“ys”。训练数据集和测试数据集都包含xs和ys,比如训练数据集的图片是mnist.train.images,训练数据集的标签是mnist.train.labels,每一张图片包含28X28个像素点,可以用一个数字数组来表示这张图片。因此,在MNIST训练数据集中,mnist.train.images是一个形状为 [60000, 784]的张量,第一个维度数字用来索引图片,第二个维度数字用来索引每张图片中的像素点。在此张量里的每一个元素,都表示某张图片里的某个像素的强度值,值介于0和1之间。
为了用于这个教程,我们使标签数据是"one-hot vectors"。 一个one-hot向量除了某一位的数字是1以外其余各维度数字都是0。所以在此教程中,数字n将表示成一个只有在第n维度(从0开始)数字为1的10维向量。比如,标签0将表示成([1,0,0,0,0,0,0,0,0,0,0])。因此,mnist.train.labels是一个 [60000, 10]的数字矩阵。
Tensorflow手写数字识别步骤
- 参数初始化
model_filepath = "model2.ckpt"
sess = tf.InteractiveSession()
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
Variable和placeholder的区别是, Variable需要初始化值, 而placeholder则不需要, 你可以在运行时通过Session.run中的feed_dict来指定值。
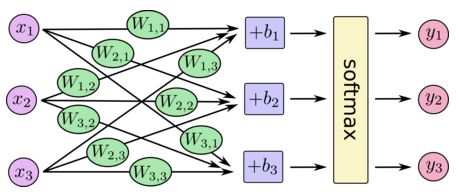
写成矩阵计算:
- 构建多层卷积网络
要构建CNN,会创建很多权重和偏置参数, 一般我们应该用小噪声的权重去初始化。为了symmetry breaking和避免0 gradients。因为我们使用的是ReLu激活函数, 用较小的正值bias来初始化可以有效地避免dead neurons。这部分会被反复使用到, 因此需要写成一个函数。
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
- 构建第一卷积层
下面的[5, 5, 1, 32],表示weight的形状, 第一和第二参数表示使用5*5的patch,第三个参数表示有一个输入通道(因为是灰度图片),第四个参数表示32个输出通道。同时, 我们有一个相应的偏置向量来对应每个输出通道。为了使用这一卷积层, 我们需要把图片输入reshape成四维的tensor [-1,28,28,1]。-1表示flat, 第二三维表示图片大小, 第四维表示颜色通道。
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1, 28, 28, 1])
接下来, 设置卷积的步长为1和SAME的padding方式, 池化采用2*2的大小. 这个也是可以复用的, 因此封装成一个function.
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
使用上面定义的卷积(使用relu激活)和池化函数计算:
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
- 第二层卷积
此时, 输入是第一卷积池化层的计算结果. 因此weight的输入channel变成了32, 输出设置为64, 同样的bias向量大小也相应设置为64.
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
- 全连接
经过前面的处理, 此时的图片size已经减到7*7, 可以使用全连接来处理整个输入了. 这里我们选择1024个神经元
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
- dropout过拟合处理
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
- 输出
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
使用 softmax 回归分类, 计算分类结果:
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
- 评估模型的方法
获取到预测值后, 我们需要了解预测值和真实结果的差距, 定义我们的cost function:
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
- 训练模型
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
sess.run(tf.initialize_all_variables())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
- 保存模型
训练结束后, 可以把结果保存成模型文件, 供以后识别图片使用.
save_path = saver.save(sess, model_filepath)