Graphx图算法【6】强联通分量StronglyConnectedComponent

强连通分量是指在有向图中，如果两个顶点 、 之间有一条从 到 的有向路径，同时还有一条从 到 的有向路径，则这两个顶点是强连通的。如果有向图G的每两个顶点都强连通则 G 是一个强连通图。有向图的极大强连通子图是该图的强连通分量。

6.1 简介

Graphx的强连通分量算法是计算一个图中所有的强连通分支，节点属性用来标识该节点所属的强连通分支，连通分支的标识是该连通分支中最小的节点id作为连通分支的id。

6.2 算法场景

社区发现：根据连通性来识别图中的子社区

6.3 算法流程

一. 通过循环不断寻找剩余图中的强连图分支，循环内部：

  （1）对图中所有节点设定初始连通分支id，用自己的节点id作为所属连通分支的id，并将所有节点打上初始标记false；

  （2）首先做循环，将只有出边或入边的节点标记为true，将 **只存在单向边的或者孤立的节点** 和 **已经确认且打好标记的强连通分量中的节点**（即被标记为true的节点）从图中去除；

  （3）为图中节点正向着色，先用节点id为自身着色，之后沿着出边向邻居节点发送自己的着色id（只有较小的着色id向较大的着色id的节点发送消息）。

  （4）为着色完成的图中节点反向打标签（是否完成连通分支id标记）。在着色完成的图中，节点id与节点所在连通分支id相同时表明该节点是着色的root节点，标记为true。若一个节点对应的入边的另外一个节点是true，则该节点也被标记为true。节点沿着入边由src节点向dst节点发送自身标记情况，只有收到true的消息则节点便标记为true。（只有着色相同，且一条边上dst节点——发消息者是true但是src节点——收消息者是false时，dst节点才会向src
  节点发送消息）

二、下面以一个具体例子说明算法流程：

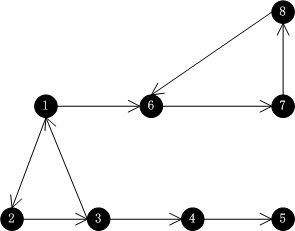
原始图

原图.png

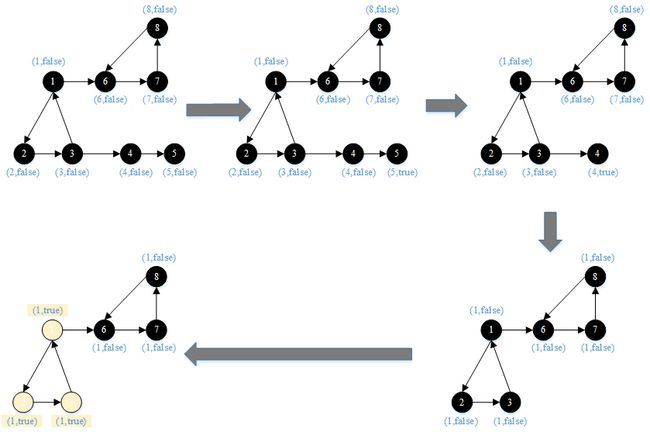
对原始图进行该算法处理，每一步得到的结果展示如下图： （每个图对应上面流程中的每个步骤）

强连通分量流程.png

第一个图对应流程步骤（1），对每个节点进行设定初始联通分支id，即初始阶段每个节点独立，各自属于各自节点id所对应的联通分支，并且所有节点的初始标记为false。

第二、三个图对应流程步骤（2），将不可能存在与强连通分支中的节点（即节点本身自己作为一个联通分支的节点，强连通分支要求分支中的节点正向联通且反向也联通，对于只有出边或入边的节点不可能形成环路。）或者已经确定好一个联通分支的节点们删除，对剩余节点进行着色和打标记。第一次循环节点5只有入边被标记为true，会被删除，第二次循环由于节点5被删除，节点4只有入边也会被标记为true之后被删除。

第四个图对应流程步骤（3），进行正向着色，沿着节点的出边方向向邻居节点发送自己的节点id，只有自己的节点id比邻居节点id小才会发送，这是为了最终一个联通分支中有个统一的id，这里是约定把一个分支中最小的节点id作为分支id（你要想用最大的节点id作为联通分支id也是可以的）。经过多次迭代后所有节点会被着色成1。

第五个图对应流程步骤（4），进行反向打标记，首先节点1由于着色id和节点id相同，所以节点1是root节点。从root节点沿着入边方向进行发送true标记，但凡能收到true标记的节点都会被标记为true。节点1可以沿着入边向节点3发送true，节点3标记为true后可以沿着入边向节点2发送true，至此该迭代结束。此时节点1，2，3完成联通分量的标记。

第一次循环结束后，再次进入循环时，节点1，2，3节点由于完成了联通分量的标记标记为了true，将会将被步骤（2）删除。而节点6，7，8还没完成连通分量的标记，在新一轮pregel迭代中中会重新用节点id为每个节点着色，并继续后续步骤（3）（4）流程。

6.4 源码分析

object StronglyConnectedComponents {
  def run[VD: ClassTag, ED: ClassTag](graph: Graph[VD, ED], numIter: Int): Graph[VertexId, ED] = {
    require(numIter > 0, s"Number of iterations must be greater than 0," +
      s" but got ${numIter}")

    // the graph we update with final SCC ids, and the graph we return at the end
    // 初始化图，将节点id作为节点属性，sccGraph是最后的返回结果图
    var sccGraph = graph.mapVertices { case (vid, _) => vid }
    // 在迭代中使用的图
    var sccWorkGraph = graph.mapVertices { case (vid, _) => (vid, false) }.cache()

    // 辅助变量prevSccGraph，用来unpersist缓存图
    var prevSccGraph = sccGraph

    var numVertices = sccWorkGraph.numVertices
    var iter = 0
    while (sccWorkGraph.numVertices > 0 && iter < numIter) {
      iter += 1
      // 此处循环内部工作：
      // 1.第一次循环进入时：将sccWorkGrpah图中只有单向边的节点或者孤立节点去掉； 后面循环进入时：将sccWorkGraph图中已经标识完成的强连通分量去掉。
      // 2.更新图中节点所属的强连通分支id
      // 只有在第一次进入第一层循环时，第一层循环内部的do-while循环才会循环多次，第2次以上只会只运行一次do{}的内容，因为后面图中不存在单向节点了。
      do {
        numVertices = sccWorkGraph.numVertices
        sccWorkGraph = sccWorkGraph.outerJoinVertices(sccWorkGraph.outDegrees) {
          (vid, data, degreeOpt) => if (degreeOpt.isDefined) data else (vid, true)
        }.outerJoinVertices(sccWorkGraph.inDegrees) {
          (vid, data, degreeOpt) => if (degreeOpt.isDefined) data else (vid, true)
        }.cache() //得到图中的有双向边的节点（vid，false）， 单向边或者孤立节点（vid，true），并且已经成功标记完连通分支的节点自身属性便是（vid，true）

        // 拿到图中只有单向边的节点和孤立节点
        val finalVertices = sccWorkGraph.vertices
            .filter { case (vid, (scc, isFinal)) => isFinal}
            .mapValues { (vid, data) => data._1}

        // write values to sccGraph
        //sccGraph[VertexId, ED]      finalVertices VertexRDD[VertexId]
        //外部第一次循环不会变动sccGraph节点的属性，只有在第二次开始才会将顶点所属的强连通分支id更新到图节点属性中。
        sccGraph = sccGraph.outerJoinVertices(finalVertices) {
          (vid, scc, opt) => opt.getOrElse(scc)
        }.cache()
        // materialize vertices and edges
        sccGraph.vertices.count()
        sccGraph.edges.count()
        // sccGraph materialized so, unpersist can be done on previous
        prevSccGraph.unpersist(blocking = false)
        prevSccGraph = sccGraph

        // 只保留属性attr._2为false的节点（这些节点是未完成连通分量打标签的节点，后面进入pregel重新着色）
        sccWorkGraph = sccWorkGraph.subgraph(vpred = (vid, data) => !data._2).cache()
      } while (sccWorkGraph.numVertices < numVertices) //图中存在单向边的节点，节点被删除变少了，则继续循环

      // 如果达到迭代次数则返回此时的sccGraph，将不再进入pregel进行下一步的着色和打标签。
      if (iter < numIter) {
        // 初始用vid为自身节点着色，每次重新进入pregel的图将重新着色
        sccWorkGraph = sccWorkGraph.mapVertices { case (vid, (color, isFinal)) => (vid, isFinal) }
        sccWorkGraph = Pregel[(VertexId, Boolean), ED, VertexId](
          sccWorkGraph, Long.MaxValue, activeDirection = EdgeDirection.Out)(
          // vprog： 节点在自己所属连通分支和邻居所属分支中取最小者更新自己。
          (vid, myScc, neighborScc) => (math.min(myScc._1, neighborScc), myScc._2),
          // sendMsg：正向（out）向邻居传播自身所属的连通分支（只有当自己所属连通分支比邻居小才会发送消息）
          e => {
            if (e.srcAttr._1 < e.dstAttr._1) {
              Iterator((e.dstId, e.srcAttr._1))
            } else {
              Iterator()
            }
          },
          // mergeMsg： 多条消息（邻居的连通分支）取最小者
          (vid1, vid2) => math.min(vid1, vid2))

        //第二个pregel：为着色后的节点打标签，final表示该节点的连通分支id已经标记完成。
        sccWorkGraph = Pregel[(VertexId, Boolean), ED, Boolean](
          sccWorkGraph, false, activeDirection = EdgeDirection.In)(
          // vprog： 如果节点id和所属连通分支id相同，则该节点是root
          //         root节点是完成连通分支标记的节点，是final （final是被标记为true）
          //         如果节点和final节点是邻居（收到的消息是final），则该节点也是final
          (vid, myScc, existsSameColorFinalNeighbor) => {
            val isColorRoot = vid == myScc._1
            (myScc._1, myScc._2 || isColorRoot || existsSameColorFinalNeighbor)
          },
          // 从完成着色的分量的root开始，反向（in）遍历节点，当一条边上两个节点的着色不同时则不发送消息。
          e => {
            val sameColor = e.dstAttr._1 == e.srcAttr._1
            val onlyDstIsFinal = e.dstAttr._2 && !e.srcAttr._2
            if (sameColor && onlyDstIsFinal) {
              Iterator((e.srcId, e.dstAttr._2))
            } else {
              Iterator()
            }
          },
          // mergeMsg
          (final1, final2) => final1 || final2)
      }
    }
    sccGraph
  }

}