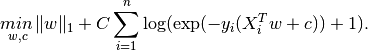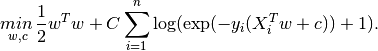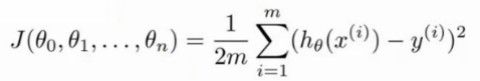本节不仅介绍了Logistic回归在sklearn中模型应用,还介绍了liblinear、牛顿法、拟牛顿法(DFP算法、BFGS算法、L-BFGS算法)、梯度下降、随机梯度下降等,正文如下,欢迎围观喔~~(我的字迹请大家别吐槽了,已放弃治疗,捂脸~`~)
上一篇主要是学习了Logistic回归(Logistic Regression)算法笔记(一)-Python,用基础Python实现了Logistic回归算法。本文将利用scikit-learn中的相关模块学习Logistic回归算法的实现
在scikit-learn中,主要是基于LogisticRegression模型来解决Logistic回归算法,其中,有两种不同的代价函数(cost function):
L1:
L2:
对于L1、L2两式子的解释:每个式子中前面那项是正则化项(Regularizer)(包含w的范数),后面那项是损失函数(loss function),参数C控制了两者在最终的损失函数中所占的比重。求解w参数的方法根据L1/L2代价函数的不同,也存在不同的求解拟合参数的方法:
1)‘liblinear’->liblinear是一个针对线性分类场景而设计的工具包,支持线性的SVM和Logistic回归等,但是无法通过定义核函数的方式实现非线性分类。
备注:libSVM是一套完整的SVM模型实现。用户可以在libSVM中使用核函数来训练非线性的分类器,当然也能使用更基础的线性SVM。由于支持核函数的扩展,libSVM理论上具有比liblinear更强的分类能力,能够处理更为复杂的问题。但是针对线性分类,liblinear无论是在训练上还是在预测上,都比libSVM高效得多。此外,受限于算法,libSVM往往在样本量过万之后速度就比较慢了,如果样本量再上升一个数量级,那么通常的机器已经无法处理了。但使用liblinear,则完全不需要有这方面的担忧,即便百万千万级别的数据,liblinear也可以轻松搞定,因为liblinear本身就是为了解决较大规模样本的模型训练而设计的。关于libSVM和liblinear两者差异,不妨看看LIBSVM与LIBLINEAR
接下来的一些求解拟合参数的方法需要先了解牛顿法以及相关的知识等,先来简单介绍一下
牛顿法(Newton's method)又称为牛顿-拉弗森方法(Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。该方法使用函数f(x)的泰勒级数的前几项来寻找方程f(x)=0的根。
在最优化的问题中,线性最优化至少可以使用单纯行法求解,但对于非线性优化问题,牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f,求函数f的极大极小问题,可以转化为求解函数f的导数f'=0的问题,这样求可以把优化问题看成方程求解问题(f'=0)。剩下的问题就和第一部分提到的牛顿法求解很相似了。如果是高维情况,那么牛顿法的迭代公式见图3:
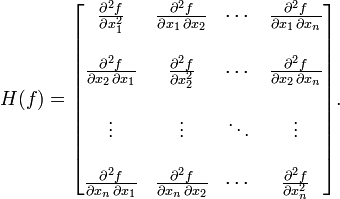
图3中的H表示Hessian矩阵,见图4
在上面牛顿法公式的得出过程中,其实用到了凸优化的知识,关于凸优化的知识,如果时充裕,建议看(Convex-optimization)凸优化-英文版,这个电子版是免费下载的,赞!
虽然牛顿法比一般的梯度下降法收敛速度快,但是在高维情况下,计算目标函数的二阶偏导数的复杂度很大,而且有时候目标函数的海森矩阵无法保持正定,不存在逆矩阵,此时牛顿法将不再能使用。因此,人们提出了拟牛顿法。这个方法的基本思想是:不用二阶偏导数而构造出可以近似Hessian矩阵(或Hessian矩阵的逆矩阵)的正定对称矩阵,进而再逐步优化目标函数。不同的构造方法就产生了不同的拟牛顿法(Quasi-Newton Methods)。
介绍一下拟牛顿条件:
看到了吧,此时已经不需要求解二阶倒数啦,B_k+1(x_k+1-x_k)=Δf(x_k+1)-Δf(x_k)(割线方程)。上面提到根据拟牛顿条件,有不同的拟牛顿方法,具体有哪些呢:-》》DFP算法、BFGS算法、L-BFGS算法等。接下来再分别介绍一下,嘿嘿。
DFP算法:该算法是以William C. Davidon、Roger Fletcher、Michael J.D.Powell三人的首字母命名,最初由Davidon于1959年提出,随后被Fletcher和Powell研究和推广,是最早的拟牛顿法。
BFGS算法:该算法是以发明者Broyden、Fletcher、Goldfarb和Shanno四人名字的首字母命名的,BFGS算法比DFP算法更优,目前它已经成为求解无约束非线性优化问题最常用的方法之一。BFGS算法已经有较完善的局部收敛理论,对其全局收敛性的研究也取得了重要成果。
L-BFGS(Limited-memory BFGS)算法:考虑到在数据很大时,BFGS中的D_k也会占用很大的空间,因此,L-BFGS对BFGS算法进行近似:不再存储完整的矩阵D_k,而是存储计算过程中的向量序列{s_i},{y_i}需要矩阵D_k时,利用向量序列{s_i},{y_i}的计算来代替。而且也不是将向量序列{s_i},{y_i}全部储存,而是固定存储最新的n个(n可以根据用户自己机器的内存来参考)每次计算D_k时,只利用最新的n个向量序列{s_i},{y_i}。
牛顿法和拟牛顿法先介绍到这里,继续回来sklearn中的Logistic回归模型。在该模型的计算参数的方法,除了liblinear方法,接着介绍其他的:
2)lbfgs-》L-BFGS算法,如上所述
3)newton-cg-》牛顿法,如上所述
4)sag->Stochastic Average Gradient descent
好吧,又得停下来解释sag啦,关于梯度下降算法的知识,推荐大家看一篇英文博客An overview of gradient descent optimization algorithms ,隔空膜拜~~
(1)梯度下降算法(Gradient descent)
梯度:在向量微积分中,标量场的梯度是一个向量场。标量场中某一点的梯度指向在这点标量场增长最快的方向。
图10-图12中,关于梯度的介绍,见维基百科-梯度
在一些回归分析中,为了求解参数,构建了类似如图13的最优化函数,其中,h_θ(x^i)表示基于算法预估结果,J_θ(θ)表示代价函数,为了求解θ使得J_θ(θ)最小,那么就要不断对J_θ(θ)求梯度,且满足图14的迭代形式,因为每次都是当前的参数减去梯度,所以叫做梯度下降法
梯度下降方法的缺点:每一次迭代,都要使用数据集合中的全部数据,当数据量很大时,计算量非常大,导致计算速度也会很慢。因此,出现了随机梯度下降法(Stochastic gradient descent,SGD)
随机梯度下降法SGD:SGD也是利用图13-14的方式,但是每一次迭代,他不是要利用全部的数据,而是每次迭代只用一个样本,在样本量很大的情况下,可能只需要部分样本就可以求解出最好的参数了。但是也正是因为这样的随机,导致SGD的收敛速度要小于梯度下降法的收敛速度,也就是说为了达到同样的精度,SGD需要的总迭代次数要大于梯度下降。因此出现了Stochastic Average Gradient descent(SAG)这样的优化算法
随机平均梯度下降法(Stochastic Average Gradient descent,SAG):
SAG算法在内存中为每个样本都维护一个旧的梯度y_i,随机选择一个样本i来更新d,并用d来更新参数x。具体来说,更新的项d来自于用新的梯度f^'_i(x)替换d中的旧梯度y_i,这就是
的意思。如此,每次更新的时候仅仅需要计算一个样本的梯度,而不是所有样本的梯度。计算开销与SGD无异,但是内存开销要大得多。已经证明SAG是一种线性收敛算法,这个速度远比SGD快。
嗯,在sklearn中求解Logistic回归中参数的方法基本就是这些,终于可以开始讨论Logistic回归模型了~~呀比~
Logistic回归模型-LogisticRegression
classsklearn.linear_model.LogisticRegression(penalty='l2',dual=False,tol=0.0001,C=1.0,fit_intercept=True,intercept_scaling=1,class_weight=None,random_state=None,solver='liblinear',max_iter=100,multi_class='ovr',verbose=0,warm_start=False,n_jobs=1)
别晕,马上是参数分析:
1)penalty->代价函数,默认是上面提到的L2;
2)dual->默认是false。如果是true,则表示使用‘Dual formulation’,这种情况仅仅适合于penalty='l2'且solver用的是liblinear的情况;只要样本数大于特征数值,最好将dual=false
3)tol->停止条件(Tolerance for stopping criteria)。默认为float,default: 1e-4
4)C->见T图1-2中的C,C越大,那么表示每个式子中左部分的正则化在整个代价函数中占得比重就更小,默认为1.0,必须是正的浮点数(a positive float)
5)fit_intercept->bool, default: True。 Specifies if a constant (a.k.a. bias or intercept) should be added to the decision function.表示是否添加特征值,与下面的intercept_scaling有关
6)intercept_scaling->float,默认是1.0。intercept_scaling属性起作用的条件:solver是'liblinear' 并且fit_intercept=true。那么在这种条件下,特征向量X就变为了[X,intercept_scaling],相当于多了一个合成的特征值
7)class_weight->dict or ‘balanced’, default: None. 默认None表示所有的y类别权重一致
8)max_iter->最大迭代次数,默认为100;此值仅仅当solver是“newton-cg,sag,或者lbfgs”
9)solver->{'newton-cg','lbfgs','liblinear','sag'},默认取值是'liblinear'。关于这四种求解参数的方法,他们与代价函数L1,L2之间的试用关系见图17
解释:(1)如果数据集比较小,那么利用'liblinear'就可以啦;(2)sag在处理大数据集时速度更快;(3)如果不是二分类,而是多种y类型的区分,那么liblinear就不适合了,只能用剩下的三种了;(4)'newton-cg','lbfgs','sag'这三种solver只可以处理代价函数是L2的情形;(5)在使用 ‘sag’方法时,最好将各个特征的取值利用sklearn.preprocessing先处理为数量级是一个范围的,比如都为0-1之间的,这样才能有效的保证sag方法在使用时具有较快的收敛速度。
10)multi_class->str, {‘ovr’, ‘multinomial’}, default: ‘ovr’,这个参数是针对多元分类(二元以上,所以不包括solver='linlinear')。‘ovr’表示binary拟合(大概就是每一类要不是0,要不是 1);‘multinomial’表示在拟合过程中,the loss minimised is the multinomial loss fit across the entire probability distribution.(非常不熟悉多类分类,所以不清楚这个设置到底啥意思,请大神指点,我也会在以后慢慢了解)
11)verbose->冗余值,非负整数, default: 0。仅仅在solver为linlinear或者lbfgs时,设置该取值
12)warm_start->When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. Useless for liblinear solver.
终于可以写代码了,好开心 · · ·
栗子:继续以sklearn的dataset中的iris数据集来计算,取其前两个特征:
1)准备数据
2)利用数据,训练Logistic回归模型
3)在两个特征值的取值范围内,构建网格,产生一些介于最值之间的等差数据数组
4)预测网格内的数据
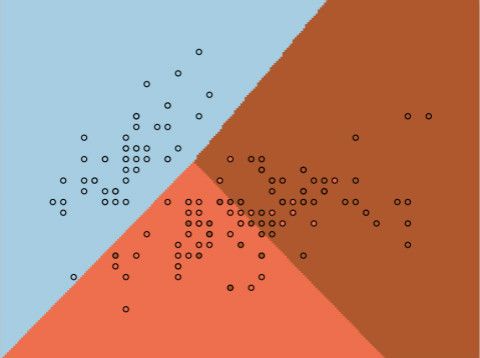
5)绘制边界
在上图的绘制中,用到了pcolormesh()函数,它类似于pcolor()函数,也是最坐标点就行着色,但是不同的是:
因为此次分类中,y的取值为0,1,2三类,所以对应的上图24中有三种颜色。
本来还想再写一个sklearn中的Logistic回归的例子,但是限于篇幅,这篇文章太长了,以后深入分析的时候再举例~`~
好哒,这篇先到这里,希望有点用途,也希望大神们不吝赐教,谢谢大家啦~~