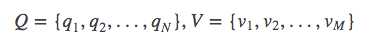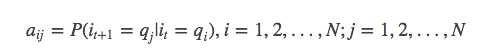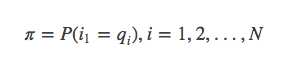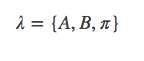在大学学习<概率论和数理统计>的时候,我们就已经学习过马尔科夫链,这里对于马尔科夫链就不多做赘述,而今天这一篇文章所要概括的是隐马尔科夫模型(HMM).
ps:马尔科夫的彼得堡数学学派挺有意思,有兴趣的可以找一些相关资料拓展一下
一:隐马尔克夫模型应用
隐马尔科夫模型在语音识别上是一种非常成功的一种技术,在自然语言理解上已经运用的非常成熟,由于HMM的诸多优点,我们在以下几个领域应用后有了很不错的成绩:
1:分词处理
分词处理在我们生活中很常见,比如在一个句子中,每一个现在的词是HMM的一个状态,而词语的产生是被看做选择状态,然后再由当前词输出词的一个二重随机过程
2:信息处理
比如我们常常使用的百度,每一次输入关键词进行搜索,就可以看作是一个马尔科夫过程,就好像是用户选择状态,然后根据现在的状态和自己的需求,产生后续的状态.
3:词性识别
这个过程比较复杂,就好比一个词语在不同的语句中会涉及到不同的词性,而这个需要一个很复杂的模型,以便于更多的获取上下文信息然后进行状态选取.
二:隐马尔科夫模型简介
在大学概率论与数理统计的学习中我们学习过马尔科夫链以及随机过程,这里就不再赘述,在马尔科夫模型中,每一个状态必须要对应一个可以观察的事件,这样应用起来往往很不方便,在隐马尔科夫中,使得可观察的是一个概率函数,并且状态本身是不可以观察,这样的话HMM中就包含了双重随机过程,一个是系统状态的变化,一个是状态决定观察的随机过程.
一个HMM,包括了一下的一些要素:
①:设Q是所有可能的状态的集合,V是所有可能的观测的集合。
②:N是可能的状态数,M是可能的观测数,其中状态q是不可见的,状态V是可见的
③:I是长度为T的状态序列,O是对应的观测序列
④:A为状态转移概率矩阵,并且:
A=[aij]N*N
是在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。 这实际在表述一个一阶的HMM,所作的假设是每个状态只跟前一个状态有关。
⑤:B是观测概率矩阵:
其中:
是在时刻t处于状态qj的条件下生成观测vk的概率。 观测是由当前时刻的状态决定的,跟其他因素无关,
π是初始状态概率向量:
其中:
最后:
隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定,π和A决定状态序列,B决定观测序列。因此,隐马尔可夫模型λ可以用三元符号表示,即
状态转移概率矩阵A与初始状态概率向量π确定了隐藏的马尔可夫链,生成不可观测的状态序列。观测概率矩阵B确定了如何从状态成观测,与状态序列综合确定了如何产生观测序列.
在给定上述的N,A,M,B和π之后,便可以确定一个HMM,比如一个(N=3)的HMM,就可以表示为:
通常情况下,如果两个状态之前的转移概率是0,就不画出他的路径
HMM依照其产生的观测值,一般可以分为离散HMM和连续HMM,我们在自然语言处理中一般使用的都是离散HMM,因为连续HMM产生输出的是实数或者实数组成的向量X,而我们自然语言处理中的绝大多数都是对离散型进行处理,连续性仅仅在语音识别检索中使用,并且计算基本相同,我们将着重在离散型的HMM上处理.
而这个部分的确挺困难,我也在慢慢摸索,以后有新的体会一定分享给大家.
提前祝大家新年快乐!
2018年继续加油!
参考书目:
李航<统计学习方法>
推荐一个博主:
I Love Natural Language Processing