Matrix4矩阵变化
连载:flutter布局-1-column
连载:flutter布局-2-row
连载:flutter布局-3-center
连载:flutter布局-4-container
这个是用来变换的矩阵,总计需要16个参数也可以理解成4*4的矩阵。
具体有以下参数:
scale:缩放比例
transform: 移动
rotationZ:绕Z轴旋转
rotationX:绕X轴旋转
rotationY:绕Y轴旋转
columns:设置一个新的矩阵
compose:复合平移、旋转、缩放,形成新的状态
copy:复制一个4*4的张量(矩阵)
4*4矩阵:
Matrix4(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)
1、scale:缩放比例 transform: Matrix4.diagonal3Values(2, 10, 1),
Matrix4.diagonal3Values(1, 1, 1)
表示缩放的比例,分别沿x,y,z三个方向,x轴正向向右,y轴正向向下,z轴正向从屏幕朝上,正值表示正向,>1表示放大,小于1大于0表示缩小,负值表示反向。
上面的值红框的宽高都是80,里面的小框宽高都是30,缩放的时间这样更能体现两个的相对位置。
具体的使用方法或者值,大家可以仔细看下上面的图片。
Z轴的变化在平面手机上看不出效果,后面我们在做旋转的时间可以具体看下z轴的变化。
缩放有以下几种写法:
举个例子:向x轴正向放大2倍。
Matrix4.diagonal3Values(2, 1, 1)Matrix4.diagonal3(v.Vector3(2, 1, 1))Matrix4.diagonal3(v.Vector3.array([2, 1, 1]))-
Matrix4(2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)
上述三种写法都表示向x轴正方向移动30个单位距离。
第2、3两中写法是用三维向量表示的,但是需要导入向量包
import 'package:vector_math/vector_math_64.dart' as v;
第4中写法是4*4的矩阵写法:
其中矩阵的第1、6、11个值分别代表的是x轴缩放、y轴缩放、z轴缩放
2、transform: 移动
表示平移的距离,分别沿x,y,z三个方向,
x轴正向向右,
y轴正向向下,
z轴正向从屏幕朝上,
正值表示正向移动,负值表示负向移动,
其中z轴移动在平面上无法看出小错
移动有以下几种写法:
举个例子:向右移动30个单位的距离。
Matrix4.translationValues(30, 0, 0)Matrix4.translation(v.Vector3(30, 0, 0))Matrix4.translation(v.Vector3.array([0, -30, 0]))-
Matrix4(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 30, 0, 0, 1)
上述三种写法都表示向x轴正方向移动30个单位距离。
第2、3两中写法是用三维向量表示的,但是需要导入向量包
import 'package:vector_math/vector_math_64.dart' as v;
第4中写法是4*4的矩阵写法:
其中矩阵的第13、14、15个值分别代表的是x轴平移、y轴平移、z轴平移
3、rotationZ:绕Z轴旋转
绕着Z轴旋转,正向是顺时针,负向是逆时针,
正向也就是从x轴正向往y轴正向旋转
两种写法:
-
Matrix4.rotationZ(pi / 6), 参数是弧度 -
Matrix4(cos(pi / 6), sin(pi / 6), 0, 0,-sin(pi / 6), cos(pi / 6), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1), 参数是弧度。
也就是改变 1、2、5、6这个4个值
其中1、6的值相同,为cos值
2、5相反,2位sin值,5为-sin值
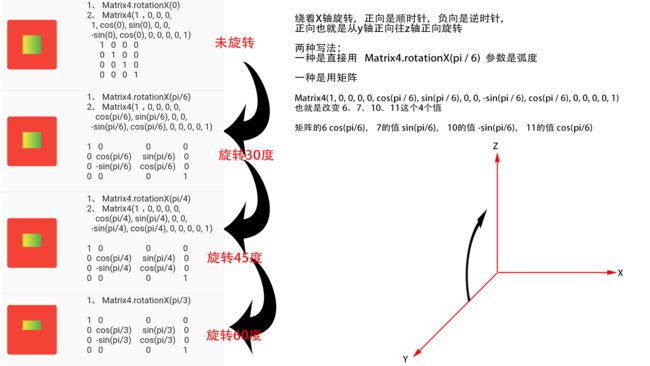
4、rotationX:绕X轴旋转
绕着X轴旋转,正向是顺时针,负向是逆时针,
正向也就是从y轴正向往z轴正向旋转
两种写法:
-
Matrix4.rotationX(pi / 6), 参数是弧度 -
Matrix4(1, 0, 0, 0, 0, cos(pi / 6), sin(pi / 6), 0, 0, -sin(pi / 6), cos(pi / 6), 0, 0, 0, 0, 1), 参数是弧度。
也就是改变 6、7、10、11这个4个值
矩阵的6 cos(pi/6), 7的值 sin(pi/6), 10的值 -sin(pi/6), 11的值 cos(pi/6)
5、rotationY:绕Y轴旋转
上图的右下角坐标系表示:
左侧灰色大小是原形状
蓝色是绕Y轴旋转30°的形状
红色虚线是投影虚线
红色实线是旋转后在xy平面
也就是手机屏幕上的投影
0-90 正向旋转角度越大,最终在手机上的投影越小,90°的时间就是一条线,而线的点是无限小的,肉眼是看不到的,所以会出现90°没有东西存在的情况。
如果想看90°的效果,就把角度改成 178*pi/180,就会出现一条线
绕着Y轴旋转,正向是顺时针,负向是逆时针,
正向也就是从x轴正向往z轴正向旋转
两种写法:
-
Matrix4.rotationY(pi / 6), 参数是弧度 -
Matrix4(cos(pi / 6), 0, -sin(pi / 6), 0, 0, 1, 0, 0, sin(pi / 6), 0, cos(pi / 6), 0, 0, 0, 0, 1), 参数是弧度。
也就是改变 1、3、9、11这个4个值
矩阵的1 cos(pi/6), 3的值 -sin(pi/6), 9的值 sin(pi/6), 11的值 cos(pi/6)
6、columns:设置一个新的矩阵
Matrix4.columns(
v.Vector4(1, 0, 0, 0),
v.Vector4(0, 1, 0, 0),
v.Vector4(0, 0, 1, 0),
v.Vector4(0, 0, 0, 1))
需要导入 import 'package:vector_math/vector_math_64.dart' as v;
4个参数都是一个4维的向量,也就是一个4个值的一维数组.
跟直接设置 Matrix4(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)是一样的效果
7、compose:复合平移、旋转、缩放,形成新的状态
Matrix4.columns(
Vector3 translation,
Quaternion rotation,
Vector3 scale)
第一个平移参数是三维向量:v.Vector3(30,0,0),表示向右移动30个单位的距离,影响的是矩阵的13,14,15三个数值;
第二个参数是4维向量,在旋转里面也可以叫四元数,进行旋转的计算,四元数和欧拉角可以相互转换,影响矩阵的参数有 1、2、3、5、6、7、9、10、11,也就是说这几个参数是影响旋转的。
从上面的旋转rotationxyz可以看出:
x轴旋转影响的参数是 6、7、10、11
y轴旋转影响的参数是 1、3、9、11
z轴旋转影响的参数是 1、2、5、6
第三个参数是一个三维向量:进行缩放的,影响矩阵的 1、6、11。
所以缩放是和旋转相关的,从上面旋转的图片结果可以看出,
计算的方法是先拿平移的参数和旋转的四元素进行计算,然后在进行缩放
8、copy:复制一个4*4的张量(矩阵)
Matrix4.copy( Matrix4(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1) )
9、identity:恢复初始状态,也就是4*4的单位矩阵
Matrix4.identity()
10、inverted:取相反的矩阵,就是反着来
你要往东,结果就往西
Matrix4.inverted(Matrix4(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 30, 0, 1))
里面的矩阵表示y轴向下移动30个单位距离
取反后是沿着y轴向上30个单位距离
Matrix4.inverted(Matrix4(2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1))
里面的矩阵表示 x轴 放大两倍,也就是所有的坐标都*2
取反后是沿着x轴缩小1倍,也就是所有的坐标*0.5
其中6,7,8,9,10的示例如下:
11、outer(合并)、skew(扭曲)、skewX(x轴扭曲)、skewY(y轴扭曲)、zero(置零矩阵)、fromList(将一个16位的一维数组转换成4*4的矩阵)
* outer 两个4维向量的乘积合并
* skew:扭曲
* skewX:沿着x轴扭曲
* skewY:沿着y轴扭曲
* zero: 全是0的4*4的张量
* fromList: 将一个16位的一维数组转换成4*4的矩阵