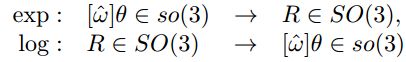指数映射

 旋转变换的指数形式

 　　用单位向量$\hat{\omega}$代表旋转轴，以及$\theta$代表绕该轴的旋转角度。则可以用三维向量$\hat{\omega}\theta\in\mathbb{R}^3$以指数形式来描述旋转。如果将$\hat{\omega}$和$\theta$分开描述，即为Axis-Angle形式。用$\hat{\omega}\theta$来描述旋转矩阵R可以有下面几种理解方法：

1. 某坐标系初始与参考坐标系{s}重合，绕轴$\hat{\omega}$旋转$\theta$角度后当到达当前姿态，其相对于{s}的旋转矩阵为R。这种描述方法为 Axis–angle representation
   
2. 角速度矢量$\hat{\omega}\theta$ 在参考坐标系{s}中描述，某坐标系初始与参考坐标系{s}重合，以角速度$\hat{\omega}\theta$转动，经过单位时间到达当前姿态（可由矩阵R表示）。
3. 角速度矢量$\hat{\omega}$在参考坐标系{s}中描述，某坐标系初始与参考坐标系{s}重合，以角速度$\hat{\omega}$转动，经过$\theta$时间到达当前姿态（可由矩阵R表示）。

•  Essential Results from Linear Differential Equations Theory
  

　　考虑下面的一阶线性微分方程：$$\dot{x}(t)=Ax(t)$$

　　其中，$x(t)\in\mathbb{R}^n$，$A\in\mathbb{R}^{n\times n}$是一个常量矩阵。若给出初始条件$x(0)=x_0$，则可得到微分方程的解为：$$x(t)=x_0e^{At}$$

　　矩阵指数$e^{At}$可以根据泰勒展开式来计算：$$e^{At}=I+At+\frac{(At)^2}{2!}+\frac{(At)^3}{3!}+...$$

　　如果矩阵$A$可以表达成$A=PDP^{-1}$，$P$为可逆矩阵，则有：

$$\begin{align*} e^{At}&=I+At+\frac{(At)^2}{2!}+\frac{(At)^3}{3!}+...\\
&=I+(PDP^{-1})t+(PDP^{-1})(PDP^{-1})\frac{t^2}{2!}+...\\
&=P(I+Dt+\frac{(Dt)^2}{2!}+...)P^{-1}\\
&=Pe^{Dt}P^{-1}
\end{align*}$$

 　　更进一步，如果$A$可以对角化，即$D$是对角矩阵：$D=diag\{d_1,d_2,...,d_n\}$，则$e^{Dt}$可以很方便的计算：

$$e^{Dt}=\begin{bmatrix}
e^{d_1t} & 0 & \cdots & 0 \\
0 & e^{d_2t} & \cdots & 0 \\
\vdots & \vdots & \ddots &\vdots \\
0 & 0 & \cdots & e^{d_nt}
\end{bmatrix}$$

•  Exponential Coordinates of Rotations

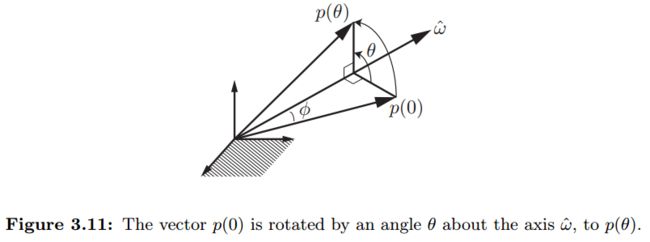
 　　参考下图中的描述，假设三维向量$p(0)$绕着转轴$\hat{\omega}$旋转$\theta$度后到达$p(\theta)$。用$p(t)$代表$t$时刻向量$p$的位置，则该过程也可以描述为：$p(0)$以角速度$\hat{\omega}$旋转（$\hat{\omega}$为单位角速度），从$t=0$运动到$t=\theta$。

 　　旋转时的速度可用$\dot{p}$来描述，且有：$$\dot{p}=\hat{\omega}\times p$$

　　用斜对称矩阵$[\hat{\omega}]$可以将向量叉乘变为矩阵与向量乘法，因此上面的微分方程可写为：$$\dot{p}=[\hat{\omega}]p$$

 　　若$\hat{\omega}=[\omega_x,\omega_y,\omega_z]^T$，定义斜对称矩阵$[\hat{\omega}]$：

$$[\hat{\omega}]=\begin{bmatrix}
0 & -\omega_z & \omega_y \\
\omega_z & 0 & -\omega_x\\
-\omega_y & \omega_x & 0
\end{bmatrix}$$

　　已知初始条件$p(0)$，该方程形式如前面研究过的$\dot{x}=Ax$，因此其解为：$p(t)=e^{[\hat{\omega}]t}p(0)$

　　由于变量$t$和$\theta$可互换，则上面方程可写为：$$p(\theta)=e^{[\hat{\omega}]\theta}p(0)$$

　　下面将$e^{[\hat{\omega}]t}$进行泰勒展开，计算斜对称矩阵$[\hat{\omega}]$的幂可得关系式：$[\hat{\omega}]^3=-[\hat{\omega}]$，利用这一关系我们可以将$[\hat{\omega}]^3$替换为$-[\hat{\omega}]$，$[\hat{\omega}]^4$替换为$-[\hat{\omega}]^2$，$[\hat{\omega}]^5$替换为$-[\hat{\omega}]^3$...于是可以得到：

$$\begin{align*} e^{[\hat{\omega}]\theta}&=I+[\hat{\omega}]\theta+[\hat{\omega}]^2\frac{\theta^2}{2!}+[\hat{\omega}]^3\frac{\theta^3}{3!}+...\\ &=I+(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-...)[\hat{\omega}]+(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}-\frac{\theta^6}{6!}-...)[\hat{\omega}]^2\end{align*}$$

　　根据正弦和余弦函数的泰勒展开式：

$$\begin{align*} \sin\theta&= \theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-...\\
\cos\theta&=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-...\end{align*}$$

　　可以将上面公式进行简化。给定$\hat{\omega}\theta\in\mathbb{R}^3$，其中$\theta$为任意标量，$\hat{\omega}\in\mathbb{R}^3$且为单位向量。则根据$[\hat{\omega}]$、$\theta$进行旋转的旋转矩阵为：$$\boxed{Rot(\hat{\omega},\theta)=e^{[\hat{\omega}]\theta}=I+\sin\theta[\hat{\omega}]+(1-\cos\theta)[\hat{\omega}]^2}$$

　　该公式也称为Rodrigues’ formula（罗德里格斯公式） 。

 　　举个例子，下图中坐标系{b}相对于固定参考坐标系{s}的姿态可以描述为：初始时刻两坐标系一致，{b}绕单位向量$\hat{\omega_1}=(0,0.866,0.5)$旋转$\theta_1=30^°=0.524rad$后到达当前姿态。

　　则{b}相对于{s}的旋转矩阵可以计算为：

$$\begin{align*}
R&=e^{[\hat{\omega_1}]\theta_1}=I+\sin\theta_1[\hat{\omega_1}]+(1-\cos\theta_1)[\hat{\omega_1}]^2 \\
&=I+0.5\begin{bmatrix}0&-0.5&0.866\\0.5&0&0\\-0.866&0&0\end{bmatrix}+0.134\begin{bmatrix}0&-0.5&0.866\\0.5&0&0\\-0.866&0&0\end{bmatrix}^2\\
&=\begin{bmatrix}0.866&-0.250&0.433\\0.250&0.967&0.058\\-0.433&0.058&0.899\end{bmatrix}
\end{align*}$$

　　坐标系{b}的姿态可由矩阵$R$描述，或者由单位向量$\hat{\omega_1}=(0,0.866,0.5)$以及转角$\theta_1=0.524rad$来描述，即旋转矩阵R的指数坐标为$\hat{\omega_1}\theta_1=(0,0.453,0.262)$

　　在Mathematica中RotationMatrix函数可以根据转轴和转角计算旋转矩阵：

•  Matrix Logarithm of Rotations

　　如果向量$\hat{\omega}\theta\in\mathbb{R}^3$表达了旋转矩阵R的指数坐标，则斜对称矩阵$[\hat{\omega}\theta]=[\hat{\omega}]\theta$是旋转矩阵R的对数。矩阵的对数是矩阵指数的逆：

　　当转角$\theta$不为$\pi$的整数倍时，可以根据旋转矩阵R计算出转轴：$$\begin{align*} \hat{\omega_x}=\frac{1}{2\sin\theta}(r_{32}-r_{23})\\\hat{\omega_y}=\frac{1}{2\sin\theta}(r_{13}-r_{31})\\\hat{\omega_z}=\frac{1}{2\sin\theta}(r_{21}-r_{12})\end{align*}$$

　　或表述为斜对称矩阵形式：$$[\hat{\omega}]=\begin{bmatrix}0&-\hat{\omega_z}&\hat{\omega_y}\\ \hat{\omega_z}&0&-\hat{\omega_x}\\-\hat{\omega_y}&\hat{\omega_x}&0 \end{bmatrix}=\frac{1}{2\sin\theta}(R-R^T)$$

　　具体推导和细节可参考：Modern Robotics: Mechanics, Planning, and Control   3.2.3.3 Matrix Logarithm of Rotations 

 

 

 

 

参考：

物理引擎中的刚体转动2

四元数指数映射旋转参数化的实际应用

视觉SLAM中的数学基础 第二篇 四元数

视觉SLAM中的数学基础 第三篇 李群与李代数

李群与李代数 - part 2 指数与对数映射、李代数求导与扰动模型

Axis–angle representation

Rodrigues' rotation formula

Lie Groups for 2D and 3D Transformations

Modern Robotics: Mechanics, Planning, and Control  3.2.3 Exponential Coordinate Representation of Rotation

Lie groups, Lie algebras, projective geometry and optimization for 3D Geometry, Engineering and Computer Vision