博弈论
1.巴什博奕
2.威佐夫博弈
3.Nim
1) 普通Nim
2) Multi-Nim
3) Anti-Nim
4) 阶梯-Nim
5) 斐波那契博弈
6) nimk
4. 无向图删边游戏
5.SG
6.翻硬币问题
下面正式开始玩游戏
1.巴什博奕
问题模型: 两个人 一堆石子 轮流取 每次可以取[1 , k] 个 先取完的人胜
简化版:
每次只可以取 1 或 2 个
- 只有一个石子 先手胜
废话 - 只有两个石子 先手胜
还是废话 - 有三个石子 无论先手取一个还是取两个 都会败 此时后手必胜(
脑子不够用了) - 有四个石子 。。。。(
死机)
如果将这一堆石子(假设有 n 个) 分成 若干个 3 个一堆 和一堆 < 3 的石子
如果 n % 3 == 0 那么假设先手从第 x 堆中 取了 y 个 那后手可以取 3 - y个将这一堆取完 , 那么无论先手怎么取 ,后手都能将这一堆的石子取完 , 也就是取到最后一个石子的人一定是后手
如果 n % 3 != 0 那先手就可以把那 < 3 的一堆取完 , 然后(让后手面对那操蛋的局面)必胜
显然推广到 取[1 , m] 个石子情况显然一样
综上
ans = n % (m + 1) == 0 ? last : first
最后一点 : 如果取走最后一个石子的人输 怎么办?
可以转化成取走第 n - 1 个石子的人赢
例题
HDU 1846 (水得不能再水)
HDU 4764 (蒸发掉了0.0000000001 ml 的 \(H_2O\))
HDU 1847
象征性的放个代码。。。。。。。。。。。。。。。
#include
#include
using namespace std;
int sg[1000] , vis[1000];
int main()
{
int n;
cin >> n;
for(int i = 1 ; i <= n ; ++i)
{
memset(vis , 0 , sizeof vis);
for(int j = 0 ; (1 << j) <= i ; ++j)
vis[sg[i - (1 << j)]] = 1;
for(int j = 0 ; 1 ; ++j) if(!vis[j]) { sg[i] = j; break; }
cout << i << " " << sg[i] << endl;
}
return 0;
} 结论 n % 3 == 0 必败
else 必胜
End
2.威佐夫博弈
问题模型: 两堆石子 , 两个人 , 每次从任意一堆中拿任意多个 , 或者从两堆中拿相同多个 , 拿走最后一个的人获胜
首先 不能将两堆石子分开 , 要一起考虑
我们定义先手必输的局势就是奇异局势
第一个奇异局势是(0 , 0)
那显然(0 , k) , ( k , 0 ) , (k , k) 都不能选(不能选就是必胜 , 下同)
那下一个奇异局势 是 (1 , 2)
同样 (1 , k) (k , 1) (2 , k) (k , 2) (1 + k , 2 + k) (2 + k , 1 + k) 都不能选
那下一个奇异局势 是 (3 , 5)
........
变成二维平面就是这样。。。。

肉眼观察可得(这TM千里眼也看不出来啊)
1.\(a_k\)是之前未出现的最小自然数
2.\(b_k=a_k+k\)
证明
由找奇异局势的方法知道如果一个是在前面出现过 那与它相关的所有都不能选
也就是说 之前未出现的数可能是合法的 , 他一定合法么 , 还是根据寻找的方法可知 , 能影响
\(a_k\) 的只有(\(a_i\) + k ,\(b_i\) + k) 而他是个一次函数 , 只会覆盖一个点 , 而他有无穷个点。。。。
所以(\(a_k\) , 某) 一定有合法的 $ 某 $
假定\((a_k,a_k+k)\)是第k个奇异局势
仅需证明\((a_{k+1},a_{k+1}+k+1)\) 第\((k+1)\)个奇异局势
\((a_{k+1},a_{k+1}+k+1)\)
(1).左边取一点
因为\(a_i \ < \ a_{k+1} \ \ \ (i
所以左边少了那就把右边拿成对应的情况
(2)右边取一点
取得比较少的时候两堆之间差值减小成为 \((a_{k+1},a_{k+1}+m)\)
那么我们就拿成 \((a_m,a_m+m)\)
取得比较多的时候 右边 < 左边
那么右边就是之前出现过的一个\(a_i(i<(k+1))\)
又因为\(a_i+i=b_i
那么左边取成类似的情况
(3).两边同时取
\(a_m,a_m+k+1\) 因为\((k+1)>m\) 所以取成 $ (a_m,a_m+m) $
那这个有没有通项呢?
Beatty定理
设a,b是正无理数且1 / a + 1 / b = 1
记P = [na] | n 为任意的正整数,Q = [nb] | n 为任意的正整数
则P与Q是Z+的一个划分,即P∩Q为空集且P∪Q为正整数集合N+
\(a_i b_i\) 显然符合Beatty序列的规律
已知Beatty序列:\(an= ⌊α*n⌋,bn= ⌊β*n⌋,而bn = an + n = ⌊α*n⌋ + n = ⌊(α+1)*n⌋\),于是β = (α+1),代入1/α + 1/β = 1,解得α =(1+$ √5 $)/ 2 ≈ 1.618
即$a_i = i * (√5 + 1) / 2 $ \(b_i = a_i + i\)
所以只要判断 (大 - 小) * \((sqrt(5) + 1) / 2\) == a ? lose : win
End
3.Nim
1) 普通Nim
n 堆石子 , 第 i 堆有 \(a_i\) 个 取走最后一个人胜(不能取的人输)
\(a_1\) ^ \(a_2\) ^ ... ^ \(a_n\) == 0 ? last : first
设 S 为异或和则
若 S != 0
则 S 的二进制下最高位的 1 在奇数个堆中出现 那设 \(a_i\) 的最高位 是 S 的最高位上的 1
那 \(a_i\) ^ \(S\) < \(a_i\) 也就是说可以取走 \(a_i\) - \(a_i\) ^ \(S\) 个 , 那他之后异或和就变成了 0
若 S == 0
想要取走一些使得 S 仍 == 0
假如从第 i 堆中取 , 取完之后变成 \(b_i\) 那么 原 S == 现 S 即 \(a_i == b_i\) 与不能不取违背
水题
【POJ1704】
【luogu1247】
2) Multi-Nim
这个没有找到证明 , 打表找规律吧
规律:
\[ SG[x]=\begin{cases} x-1\ \ \ (x\%4==0)\\ x\ \ \ (x\%4==1\ or\ 2)\\ x+1\ \ \ (x\%4==3)\\ \end{cases} \ \]
#include
#include
#include
using namespace std;
int vis[10010] , sg[10010];
int main()
{
puts("please input your test_size");
int n;
cin >> n;
puts("The ans is as follows");
for(int i = 1 ; i <= n ; ++i)
{
memset(vis , 0 , sizeof vis);
for(int j = 1 ; j <= i / 2 ; ++j)
vis[sg[j] ^ sg[i - j]] = 1;
for(int j = 1 ; j <= i ; ++j) vis[sg[i - j]] = 1;
for(int j = 0 ; 1 ; ++j) if(vis[j] == 0) { sg[i] = j; break; }
printf("i : %2d -----> sg: %d \n" , i , sg[i]);
}
return 0;
} 例题
【hdu3032】
【luogu3185】
【luogu3235】
【poj2311】
3) Anti-Nim
先手必胜当且仅当:
(1)所有堆的石子数都为 1 且游戏的 SG 值为 0;
或
(2)有些堆的石子数大于 1 且游戏的 SG 值不为 0。
定义
孤单堆:一堆火柴仅有1根火柴
充裕堆:一堆火柴有大于1根火柴T态:异或和为0
S态:异或和不为0
T2态:T态当中充裕堆数>=2
T0态:T态当中充裕堆数=0
S0态:S态当中充裕堆数=0
S1态:S态当中充裕堆数=1
S2态:S态当中充裕堆数>=2不存在T1态(用颅想想就知道了)
若干定理
【定理1】:S0态,即仅有奇数个孤单堆,必败。T0态必胜。
证明:S0态,其实就是每次只能取一根。每次第奇数根都由自己取,第偶数根都由对方取,所以最后一根必由自己取。所以必败。同理:T0态必胜。
【定理2】:S1态,只要方法正确,必胜。
证明:若此时孤单堆堆数为奇数,把充裕堆取完;否则,取成一根。这样,就变成奇数个孤单堆,由对方取。由定理1,对方必输,己必胜。
【定理3】:S2态不可转一次变为T0态。
证明:充裕堆数不可能一次由2变为0。
【定理4】:S2态可一次转变为T2态。
证明:因为对于任何一个S态,总能从一堆中取出若干个使之成为T态。又因为S1态,只要方法正确,必胜。S2态不可转一次变为T0态,所以转变的T态为T2态。
【定理5】:T2态,只能转变为S2态或S1态。
证明:因为T态,取任何一堆的若干根都将成为S态。由于充裕堆不可能一次由2变为0,所以此时的S态不可能为S0态。得证。
【定理6】:S2态,只要方法正确,必胜。
S2态,就把它变为T2态。(定理4);
对方只能T2转变为S2态或S1态(定理5)。
若转变为S2,则转向①。
若转变为S1,这时己必胜(定理1)。
【定理7】:T2态 , 必输 同 6
综上
必胜态:T0,S1,S2
必败态:S0 , T2板子题 【luogu4279】
4) 阶梯Nim
存在n个从高到低排布的阶梯
我们只可以从到相邻的低阶梯移动棋子
最低阶梯的棋子就相当于拿走
例如
1.我们可以从3到2移动一个棋子
2.我们不可以从4到3移动3个棋子
3.我们可以直接从1阶梯上拿走棋子结论 ( 奇数位的石子异或起来 == 0 ?second :first )will win
证明
如果对手移动偶数位置上的石子到了奇数位 , 那可以将技术位上多出的石子移到下一个偶数位(如果是第一个台阶就是直接移走) 偶数上的石子然并卵
那考虑奇数上的石子 , 把它移到偶数位就相当于扔掉了这些石子(因为偶数位上的没什么用)
这就跟nim游戏一模一样了
5) 斐波那契博弈
有一堆个数为\(n(n>=2)\)的石子,游戏双方轮流取石子,规则如下:
1)先手不能在第一次把所有的石子取完,至少取1颗;
2)之后每次可以取的石子数至少为1,至多为对手刚取的石子数的2倍。
约定取走最后一个石子的人为赢家。
结论: 当 n 为斐波那契数列的中的某一项时 先手必败 , 否则先手必胜
数学归纳法 为了方便,我们将n记为f[i]。
1、当i=2时,先手只能取1颗,显然必败,结论成立。
2、假设当i<=k时,结论成立。
则当i=k+1时,f[i] = f[k]+f[k-1]。
则我们可以把这一堆石子看成两堆,简称k堆和k-1堆。
( 一定可以看成两堆,因为假如先手第一次取的石子数大于或等于f[k-1],则后手可以直接取完f[k],因为f[k] < 2*f[k-1] )
对于k-1堆,由假设可知,不论先手怎样取,后手总能取到最后一颗。下面我们分析一下后手最后取的石子数x的情况。
如果先手第一次取的石子数\(y>=f[k-1]/3\),则这小堆所剩的石子数小于2y,即后手可以直接取完,此时x=f[k-1]-y,则\(x<=2/3*f[k-1]\)。
我们来比较一下\(2/3*f[k-1]\)与\(1/2*f[k]\)的大小。即4 * f[k-1]与3 * f[k]的大小,对两值作差后不难得出,后者大。
所以我们得到,\(x<1/2*f[k]\)。
即后手取完k-1堆后,先手不能一下取完k堆,所以游戏规则没有改变,则由假设可知,对于k堆,后手仍能取到最后一颗,所以后手必胜。
即i=k+1时,结论依然成立。
那么,当n不是Fibonacci数的时候,情况又是怎样的呢?
这里需要借助“Zeckendorf定理”(齐肯多夫定理):任何正整数可以表示为若干个==不连续==的Fibonacci数之和。
关于这个定理的证明,感兴趣的同学可以在网上搜索相关资料,这里不再详述。
分解的时候,要取尽量大的Fibonacci数。
比如分解85:85在55和89之间,于是可以写成85 = 55 + 30,然后继续分解30 , 30在 21 和 34 之间,所以可以写成30 = 21 + 9,
依此类推,最后分解成85 = 55 + 21 + 8 + 1。
则我们可以把n写成 \(n = f[a_1]+f[a_2]+……+f[a_p]。(a_1>a_2>……>a_p)\)
我们令先手先取完f[ap],即最小的这一堆。由于各个f之间不连续,则\(a_{p-1} > a_p + 1\),则有
\(f[a_{p-1}] > 2*f[a_p]\)。即后手只能取\(f[a_{p-1}]\)这一堆,且不能一次取完。
此时后手相当于面临这个子游戏(只有\(f[a_{p-1}]\)这一堆石子,且后手先取)的必败态,即先手一定可以取到这一堆的最后一颗石子。
同理可知,对于以后的每一堆,先手都可以取到这一堆的最后一颗石子,从而获得游戏的胜利。
例题 HDU 2516
6) nimk
一次可以从 至多k堆中选意个 , 求必胜
结论
将石子数二进制拆分 , 每一位上的一加起来 , mod (k + 1) , 若全为零则 , 必败 , 否则必胜
证明
设所有石子堆得二进制下最高位上的 1 有 m 个 ,
先选这 m 个作为先手的第一次操作的一部分 , 将最高位的 1 改成 0
往后 枚举二进制位 , 如果下一位 mod (k+1)!= 0 的位上有 1 , a 个(不算已经标记的)
如果 a <= m 可以将 之前m个石子堆中的a堆的这一位改成1 , 与外界的抵消
如果 a > m 可以将 a - m 个石子堆也纳入选择的石子堆中 , 再与外界的抵消(似乎加入(a-m)/2 就可以抵消 , 但这不影响) 这是选择的石子堆有 a 个 , 因为都是在mod (k+1) 的意义下 , 所以 a <= k , 仍然是合法的(不超过k堆)
就这么一直到最后一位 , 显然 选的石子数还是不会超过 k , 也就是说结论成立。
黑白棋
也可以参照另一(二)篇证明
无向图删边游戏
先考虑在树上
一棵树上 , 进行删边 , 删完之后 ,把所有与根不相连的部分扔掉 , 删完最后一块的人获胜
另外可能不止一棵树 , 但它们的根都长在地上
为了方便 我们先引入
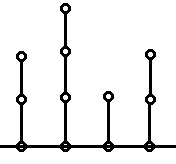
竹子(也就是链)
对于这种情况可以看成nim游戏 比如石子分别为 2 3 1 2
那对于一些复杂一些的图 , 只要能转化成竹子就行了
克朗原理
对于树上某一个点 TA的分支可以转化为以这个点为根的一个竹子
竹子长度就是 TA各个分支的边的数量的异或和
对于树上摸一个点 TA的分支可以转化为以这个点为根的一个竹子
竹子长度就是 TA各个分支的边的数量的异或和
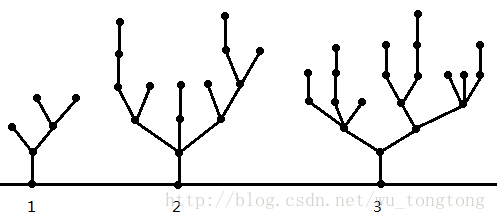
1号树 最后是一条边的竹子 \(SG_1=1\)
2号树 \(SG_2=8\)
3号树 \(SG_3=4\)
有一个证明 但是他是英文的……
克朗定理的相关证明
伪证
对于单独的链 , 他的sg值可以等价于链上边的数量 , 而一个分叉则是两个游戏的和 , 也就是一个nim游戏
再拓展到无向图上
再来一个定理
费森定理
环上的点是可以融合的 并且不改变图的SG值
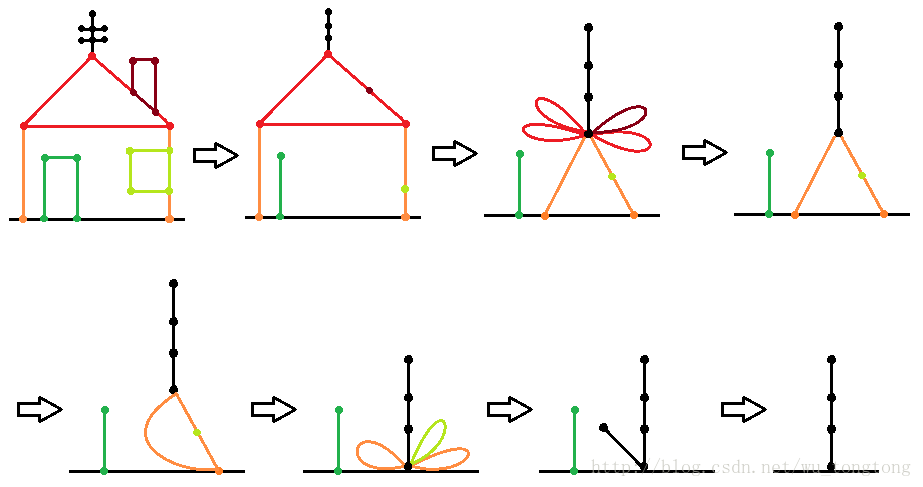
从栗子入手
门独立于大框 从门开始
地板上的两个点可以视为一个 因为地板本身就是一个大点
这样的话这扇门就成为了一个三角形 (也就是一个有三个点的环)
费森原理指出 我们可以把换上一个点等价成一个自环 而这个环又可以成为一条边
有奇数个点的环看成一条以这个点为根的边 , 偶数个的看成一个点
上一个经典的图
上图中的门就是一个奇数个点的环
最后变成一个边
右侧的窗户是一个偶数个点的环 , 变成了一个点(浅绿的那个)
知道了这两个定理 , 剩下的就是模拟了;
Christmas Game
SG
一个有向图游戏中 , u 的 sg 为 mex{ sg[v] | v 是 u 的后继节点 } , 出度为 0 的点(没有后继状态)sg = 0;
mex{A} 是 求不属于集合A的最小的 N
也就是 mex(A) = min( x | x 属于 N && x 不属于 A );
sg[i] == 0 ? 必败态 : 必胜态
如果 sg[i] == 0 , 说明 他是出度为 0 的点 || 他后面没有 sg == 0 的点 也就是说他只能转移到必胜态
否则 他一定有一个sg == 0 的后继点 , 那只需要将 他转向 sg == 0 的状态 , 他的对手就面临必败态(就死翘翘了) , 所以这是一个必胜态
求 sg 就是按定义暴力模拟 ,
//一般来讲代码差不多是这样
for(int i = 1 ; i <= n ; ++i) // 枚举要求的sg[i]
{
memset(vis , 0 , sizeof vis);
for( ; ; ) // 枚举可能的转移途径
vis[sg[v]] = 1 // 有的时候更复杂一些
int j;
for(j = 0 ; vis[j] ; ++j); /* 注意分号 */ sg[i] = j;
// 一定要从零开始 , 因为 0 代表必败态
}也可用时间戳优化一下 , 减少常数
sg 函数理论上可以求解所有的博弈论问题 , 也说明 一个游戏不用关心他具体的背景就可以 得出答案
但只是理论上 , 如果完全不关心的话 时间复杂度就会原地爆炸 QWQ
Q 游戏的和为什么是各个子游戏的sg的异或和
A 显然 , sg是由mex运算得来的也就是说这个子游戏可以转移到sg = [0 , sg[x] - 1] 的任何一个状态 , 这就和nim游戏中的石子一样可以选若干个石子取走 , 所以游戏的和的计算方式(游戏 -> 和 -> 计算方式) 就和nim游戏一样是异或起来
Q 那有的 sg 也可以转移到比当前sg大的局面 , 这不就是相当于往石子堆里加石子么? 那上面的结论还对么?
A 加石子的操作可以抵消 , 所以可以忽略加石子的操作;
6.翻硬币问题 (记结论)
link
switch(条件)
1 case 每次只能翻一个硬币
奇偶
2 case 每次能翻转一个或两个硬币(不用连续)
以 0 开始编号 , sg = 编号 , ans = ^
3 case 每次必须连续翻转k个硬币
sg[x] = x == k
4 case 每次翻动一个硬币后,必须翻动其左侧最近三个硬币中的一个,即翻动第x个硬币后,必须选择x-1,x-2,x-3 , ... x - k 中的其中一个硬币进行翻动,除非x是小于等于3的。(Subtraction Games)
sg[x] = x % (k + 1)
5 case 每次必须翻动两个硬币,而且这两个硬币的距离要在可行集S={1,2,3 .. k}中,硬币序号从0开始。(Twins游戏)
注: 没有找到关于Twins游戏的题 , 姑且认为是第二枚硬币要在第一枚左边
同上
3~5项 , 结论可以打表
[case3] case3.cpp
[case4] case4.cpp
[case5] case5.cpp
6. 每次可以翻动一个、二个或三个硬币。(Mock Turtles游戏)
结论 sg[x] = 2 * x + (x 的二进制位中1的个数 % 2 != 0)
证明
7.每次可以连续翻动任意个硬币,至少翻一个。(Ruler游戏)
结论 sg值为x的因数当中2的能达到的最大次幂。比如14 = \(2 ^ 1\) * 7,最大1次幂,即 \(2^1\) ;16= \(2 ^ 4\),最大4次幂,即\(2^4 = 16\)。
例题
分裂游戏
link
题解
最终所有的石子都会到第n个瓶子处 , 可以将石子到第n个瓶子的距离当做石子的个数
人人尽说江南好
link
题解
合并次数为奇数先手胜 , 偶数后手胜
先考虑 n <= m
如果现在轮到先手操作 , 剩下的石子 经过偶数次合并就结束了游戏 ,
设当前石子堆数最大的一堆石子为 W (其实哪一堆都可以 都是等价的)
先手有两种选择:
1.选一堆个数为一的石子堆放入W
此时后手可以模仿先手的操作
2.选两个个数为一的石子堆合并
此时后手可以将合并成的石子堆放入 W
无论哪一种合并次数都是减少了两次 , 也就是说后手必胜
先手必胜同理
这种合并方法将合并次数拉到了最长
A 为什么是选个数为一的石子堆 ?
Q 其实没啥意义 , 就是好算 , 其他的情况与这个是等价的
n > m
同样按照上面的策略将回合数拉到最长
可以假设最后的状态是只有一堆石子的石子个数小于m , 其他的都等于m
(其实还是等价 , 因为开始时石子个数都是一 , 如果有两堆石子在最后的石子数小于m , 那可以把其中一个合并成m , 这样合并次数不变)
最终的答案 = 合并次数 & 1 ? first : second
三国游戏
link
先上答案 , ans = max{每一行的次大值}
1.次大值
在选完一个人之后 , 电脑会把与这个人相匹配的最大值拿走 , 所以能得到的只是次大值
不用考虑某一行的次大值大于其他行的最大值的情况 , 那个不会对答案产生影响;
2.人必胜
电脑必胜的条件是电脑选出了某一行的最大值 , 但显然构成最大值的另一半在人的手上也就是说 , 电脑必败
江南乐
link
想想暴力
暴力枚举分成几堆
然后代码里就会有了这个东西
for(int j = 2 ; j <= i ; ++j)
{
int res = 0;
res ^= ((i % j) & 1) ? sg[(i / j) + 1] : 0;
res ^= ((j - (i % j)) & 1) ? sg[i / j] : 0;
vis[res] = tot;
}然后发现这个可以整数分块;
i % j 在 i / j 相同的情况下是一个等差数列
于是 j - i % j 也就是一个等差数列
于是考虑前两项都就可以了
Q i % j 为什么是等差数列
A i % j 就是按j分堆 , 最后剩多少 , i%(j+1) 就是按j+1 分堆 , 那可以将i%j 中拿出i/j 个分给前面
Q 为什么只用考虑前两项
A 公差是偶数 只用看第一项 , 第一项和第二项 就包含了奇偶两种情况
取石子游戏
link
这道题算是DP+博弈论
设\(L[i][j]\) 表示在 [i , j] 这段区间 左侧放\(L[i][j]\) 个石子使得 \([i - 1 , j]\) 这段区间先手必败
同理 \(R[i][j]\) 表示在右边放
大力讨论
用L表示\(L[i][j-1]\) , R表示\(R[i][j-1]\) , x 表示\(a[j]\)
- x == R \(L[i][j] = 0\)
- \(x < L , x < R\) \(L[i][j] = x\)
后手可以模仿先手进行操作 , 这样两端的两堆石子会有一堆先取完 , 假设是左边的先取完 , 也就是右边剩下一点石子 , 这时可以等价认为 , 是先手在右边有 R 个石子的状态取走了一部分 , 这时后手必胜
其余情况同理
\(\ R\ <\ x\ <\ L\)
这种情况下\(L[i][j]=x-1\)。这样子考虑,假设先手先拿了左边这一堆,那么假设还剩下了z个石子,如果z
$ L < x < R $
分析同上,\(L[i][j]=x+1\)。
\(\ x \ > \ L \ , \ x\ >\ R \\)
\(L[i][j]=x\)。还是一样的,假设先手把其中一堆拿成了z。如果z>L,R,跟着先手拿成一样多的石子则又回到了这种情况。如果\(z R同理 最后判一下 a[1] 于 $L[2][n] $ 是否想等就行了