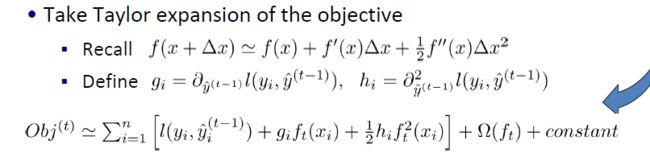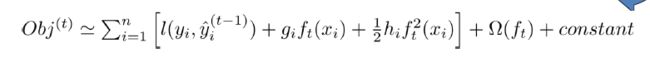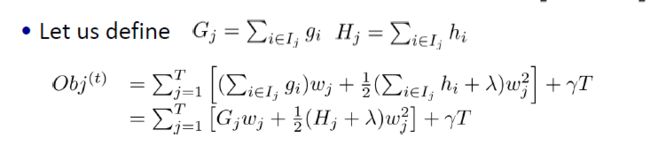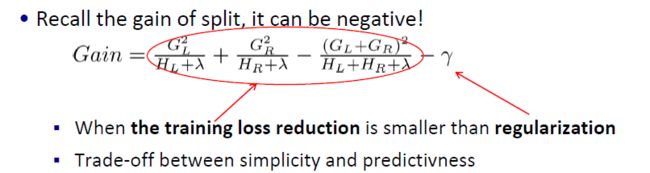Xgboost

从陈天奇的PPT中进行总结，重点了解模型的构建，策略的选择和优化算法的选取。

基础

机器学习的目标函数基本都是：

也就是损失函数和正则化项的组合。

在目标函数，偏差和方差之间做trade-off

损失函数

为了得到更好的预测模型，在训练数据集上拟合更好的效果。至少能够让我们的模型逼近训练数据的可能的分布情况。（数据的情况决定了我们模型的上界，我们尽可能的去逼近那个界）
正则化

为了得到更简单的模型，我们引入正则化。简单的模型可以让我们在预测未来的数据时候，有更小的方差，预测结果更加稳定。

回归树

也称分类回归树

决策规则与决策树相同
在每个叶子结点上都有一个分数（score）

上图可以看出来，每个叶子结点都有一个分数，那么被分到该结点的数据获得这个分数。

我们通过将多个这样的回归树集成起来，获得我们的集成算法。

上图可以看出来，对于小男孩的总体分数，就是两棵树的加和结果。

集成树的特点有：

应用非常广泛，比如GBDT 、RM。近一半的数据挖掘比赛都是使用了各种集成树算法的变体获胜的。
invariant to scaling of inputs.不是必须的进行特征归一化
能从特征中，学习到较高阶的关系
可伸缩，可很好的用在工业中（can be scalable）

模型的提出

模型假设我们有K棵树（上面提到的回归树）：

F就是我们的假设空间（函数空间，包含k个回归树）

这个模型中的参数包括：

每课树的结构，叶子结点中的score
或者使用每棵树作为参数：
与从中学习参数相反，我们去学习每个函数，即每棵树。

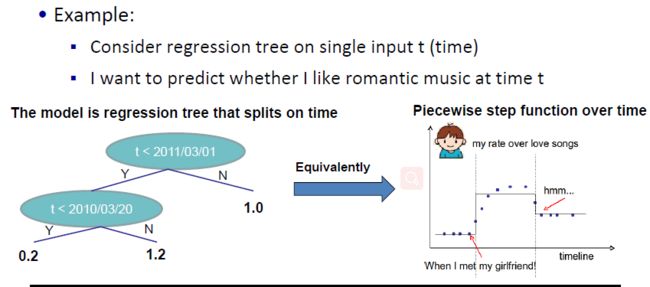
单变量分析

定义目标函数，然后去优化这个目标函数

上图中，是以时间为变量，来构建回归树，评价个人随着时间t是否喜欢浪漫音乐。

将一个回归树等价到一个分段函数中，那么我们从中需要学习的“参数”也就是我们的：

上面四幅图中，给出了不同划分位置和划分高度，最后的参数模型也就是图四的效果。

那么从一棵树开始，我们可以来定义我们模型的目标函数。

模型的目标函数

我们有K棵树

目标函数是:

第一项是我们的损失函数项，第二项是我们的正则化项。

启发式的算法

当我们讨论决策树的时候，都是启发式的从一些方面进行考虑：

通过信息增益来划分分支
剪裁树
树的最大深度
平滑叶子结点的值

我们使用决策树算法时候，就是通过信息增益来划分分支，那么这里我们可以用每一次划分的信息增益当做我们的损失函数。（划分后的信息增益-划分前的信息增益）

决策树中的剪枝，就是为了控制决策树的模型复杂度，这里我们也通过控制叶子节点的个数，来实现正则化，控制模型的复杂度。

限制树的深度，也是一定程度上限制我们的模型复杂度。

尽可能的让我们的叶子上的score平滑，使用L2正则化来控制叶子结点上的权重。

模型的学习

目标函数是:

那我们是如何学习这个目标函数的呢？

我们不能使用梯度下降算法来进行计算损失函数，因为我们这里的参数是回归树，而不是一些数值型数据（类比线性模型里面的参数 w）

从常数开始，然后每次加入一棵新树（一个新的函数）
$\hat{y}_i^{(0)} = 0 \\ \hat{y}_i^{(1)} = 0 + f_1(x_i) = \hat{y}_i^{(0)}+f_1(x_i) \\ \hat{y}_i^{(1)} = f_1(x_i) +f_2(x_i) = \hat{y}_i^{(1)}+f_2(x_i) \\ \cdots \\ \hat{y}_i^{(t)} = \sum_{k=1}^{t}f_k(x_i) = \hat{y}_i^{(t-1)}+f_t(x_i) \\$
其中，我们的是第t轮的训练模型，是t轮前我们的训练结果，是新加入的函数（新加入的一棵树）

那么我们怎么样决定一个新加入的树（函数），这个函数就是我们上面提到的我们的参数，即如何选择一个参数来优化我们的模型，当然从优化目标函数中找。

其中

是我们训练数据的标签，

是我们输入的第i个数据。

应用泰勒展开到损失函数中

上述目标函数还是很复杂，于是作者引入了泰勒展开式来替换损失函数。

1551440681216.png

类比泰勒展开式的

在我们的目标函数中损失函数相当于函数

所以我们可以得到我们的目标函数带入泰勒展开之后的结果是：

这里面是我们前t-1轮的对预测和的目标的损失，这是一个常数项。因为我们优化的是第t轮，研究怎么选择第t轮需要加进去的树，所以前面的我们都可以看作是一个常量。

给目标函数对权重求偏导，得到一个能够使目标函数最小的权重，把这个权重代回到目标函数中，这个回代结果就是求解后的最小目标函数值。

是一个叶子结点上的每一个样本的梯度值，同理理解

从我们的损失函数，说起，看我们如何定义这个，不如这里我们以简单的为例子：
$\begin{align} l(y_i,\hat{y_i}^{(t)}) & =l(y_i,\hat{y_i}^{(t-1)}+f_t(x_i))\\ & =(y_i-(\hat{y_i}^{(t-1)}+f_t(x_i)))^2 \\ & =((\hat{y_i}^{(t-1)}+f_t(x_i))-y_i)^2 \\ & = ((\hat{y_i}^{(t-1)}-y_i)+f_t(x_i))^2 \\ l((\hat{y_i}^{(t-1)}-y_i)+f_t(x_i)) & =((\hat{y_i}^{(t-1)}-y_i)+f_t(x_i))^2 \\ \end{align} \\ l((\hat{y_i}^{(t-1)}-y_i)+f_t(x_i)) 相当于f(x+\Delta x),f_t(x_i)也就是\Delta x\\ 由上面推导带入泰勒公式可以得到：\\ Obj^{(t)} = \sum_{i=1}^{n}[2(\hat{y_i}^{(t-1)}-y_i)f_t(x_i)+{f_t(x_i)}^2]+\Omega(f_t)+const \\ 对比上下两式 \\ Obj^{(t)} = \sum_{i=1}^{n}[g_if_t(x_i)+\frac{1}{2}h_i{f_t(x_i)}^2]+\Omega(f_t)+const$
针对我们的平方差损失函数来说，就是如下式子：

其中项也就是我们常说的残差项。

改善模型

从例子中理解各个参数的含义，

比如叶子结点1代表的权重（分数）是+2，叶子结点2对应的是+0.1，叶子结点3对应是-1

然后看我们的正则化项，其中T代表叶子结点的数目，从上面的例子可以很容易的计算得到我们的正则化结果。

再来看我们的目标函数

我们定义：就是第i个数据属于第j个叶子结点。

然后我们将属于同一个叶子结点的数据放入一个group里面得到

也就是将从各个样本上的遍历，映射到了对叶子结点的遍历（叶子结点里可能包含多个样本）

重新定义G 和H ，也将其从单个样本上的遍历，映射到对叶子结点的遍历。
$\begin{align} 我们将:& \\ & G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2 \\ 看作是关于w的二次函数，那么最优解是：\\ & w_j^*= -\frac{G_i}{H_i+\lambda}\\ & Obj = -\frac{1}{2}\sum_{j=1}^{T}\frac{G_j^2}{H_j+\lambda}+\gamma T \end{align}$
其中的是来评价一棵树的结构是否很好，分数越小，结构越好。

但是仍然有无数颗树可以进行选择，那么我们如何选择才能保证最优化呢？

从常数0开始，我们选择一个树加入，每一次尝试去对已有的叶子加入一个分割。

然后我们来计算分割后的结构分数（左子树+右子树）与我们不进行分割的结构分数进行做差，同时还要减去因为分割引入的结构复杂度。

对于每个节点，我们都遍历所有特征
- 对于每个特征，都按特征值将每一个数据排序
- 从左到右的线性扫描决定该特征最好的分割位置
- 将最好的分割方案适用到所有特征中。
时间复杂度分析（生成一棵深度为K的树）
- :对于每一层都需要对feature排序消耗
  
  那么每层都有d个特征需要进行分析，我们一共需要做K层。
- 可被优化的（使用近似方法？？？或者缓存根据特征的排序结果（因为生成一棵树都需要进行排序））
- can scale very large dataset

Categorical Variables

也可以很好的处理非数值型特征，并且不需要将类别特征（离散的）和数值型特征（连续的）分开进行处理。

我们可以通过one-hot编码将离散的特征类别映射到数值型。

如果类别特别多，向量会非常稀疏，但是这个算法也很擅长处理稀疏的数据。

剪枝和正则化

trade-off between simplicity and predictivness

早停止

如果最好的分裂已经出现负的Gain 停止分裂。
同时也牺牲了未来可能出现更好的分裂的情况

后剪枝

设置最大树深度，然后递归的去剪裁所有叶子节点出现负的Gain的分裂情况

总结

更细节的问题是，我们不会每个树做到最优化，这样容易过拟合，我们赋予一个参数，来控制每次的优化（不让优化效果太好），这样留下更多的优化空间给后边的树。

分类回归树的集成算法可以用来做回归，分类，ranking等等，这取决于我们的损失函数如何定义。

Xgboost比较重要的参数

（1）objective [ default=reg:linear ] 定义学习任务及相应的学习目标，可选的目标函数如下：

“reg:linear” –线性回归。
“reg:logistic” –逻辑回归。
“binary:logistic” –二分类的逻辑回归问题，输出为概率。
“binary:logitraw” –二分类的逻辑回归问题，输出的结果为wTx。
“count:poisson” –计数问题的poisson回归，输出结果为poisson分布。在poisson回归中，max_delta_step的缺省值为0.7。(used to safeguard optimization)
“multi:softmax” –让XGBoost采用softmax目标函数处理多分类问题，同时需要设置参数num_class（类别个数）
“multi:softprob” –和softmax一样，但是输出的是ndata * nclass的向量，可以将该向量reshape成ndata行nclass列的矩阵。没行数据表示样本所属于每个类别的概率。
“rank:pairwise” –set XGBoost to do ranking task by minimizing the pairwise loss

（2）’eval_metric’ The choices are listed below，评估指标:

“rmse”: root mean square error
“logloss”: negative log-likelihood
“error”: Binary classification error rate. It is calculated as #(wrong cases)/#(all cases). For the predictions, the evaluation will regard the instances with prediction value larger than 0.5 as positive instances, and the others as negative instances.
“merror”: Multiclass classification error rate. It is calculated as #(wrong cases)/#(all cases).
“mlogloss”: Multiclass logloss
“auc”: Area under the curve for ranking evaluation.
“ndcg”:Normalized Discounted Cumulative Gain
“map”:Mean average precision
“ndcg@n”,”map@n”: n can be assigned as an integer to cut off the top positions in the lists for evaluation.
“ndcg-“,”map-“,”ndcg@n-“,”map@n-“: In XGBoost, NDCG and MAP will evaluate the score of a list without any positive samples as 1. By adding “-” in the evaluation metric XGBoost will evaluate these score as 0 to be consistent under some conditions.

（3）lambda [default=0] L2 正则的惩罚系数

（4）alpha [default=0] L1 正则的惩罚系数

（5）lambda_bias 在偏置上的L2正则。缺省值为0（在L1上没有偏置项的正则，因为L1时偏置不重要）

（6）eta [default=0.3]
为了防止过拟合，更新过程中用到的收缩步长。在每次提升计算之后，会直接获得新特征的权重。 eta通过缩减特征的权重使提升计算过程更加保守。缺省值为0.3
取值范围为：[0,1]

（7）max_depth [default=6] 数的最大深度。缺省值为6 ，取值范围为：[1,∞]

（8）min_child_weight [default=1]
孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束。在现行回归模型中，这个参数是指建立每个模型所需要的最小样本数。该参数越大算法越保守。
取值范围为: [0,∞]

Xgboost原理分析