前段时间看到生成凸包的Graham算法,查了一些资料,没看到c#版的,于是想动手写一个,该程序草草完成,其中有值得优化的地方,诸位可自行改正。
Graham算法的原理:
(1)给定一个点集P={P0,P1,.....Pn),找出点集中Y值最小的点,如果Y值最小的点有多个,可选择其中X值最小的
(2)假设上一步找出的点位P0,现在对剩下的点进行极角排序,按逆时针(本程序是这样,其他的方式是一样的)极角从小到大排序,假定排序结果集为{p1,p2,p3,p4,....pn}。注意,这里不一定有N个点,因为可能存在几个点的极角相同,这时取据P0距最远的点,也或者你设定了一个极角阈值,当两个点的极角差小于该阈值时,取据P0距离远的点,这时生成的凸包有一点点误差,误差的大小取决于你设置的阈值。本程序没采用阈值,所以生成的凸包理论上不存在误差。
在进行极角排序时,不需要真的算法每个点的极角(注意,这里的极角是该点与P0相对于X轴的夹角),只需要使用向量叉积来判断即可,这个过程我使用了链表来存储排序结果,因为这个过程会进行频繁的插入。
(3)将p0,p1,p3入栈,p0,p1这两个点肯定在凸包上(原因很简单,p0不用解释了吧,p1因为它是极角最小的且为第一个点),p2则不一定在凸包上,然后进行循环(for(int i=2;i
下面是整个代码:
算法部分:
class ConvexAogrithm
{
private List nodes;
private Stack sortedNodes;
public PointF[] sor_nodes;
public ConvexAogrithm(List points)
{
nodes = points;
}
private double DistanceOfNodes(PointF p0, PointF p1)
{
if (p0.IsEmpty || p1.IsEmpty)
return 0.0;
return Math.Sqrt((p1.X - p0.X) * (p1.X - p0.X) + (p1.Y - p0.Y) * (p1.Y - p0.Y));
}
public void GetNodesByAngle( out PointF p0)
{
LinkedList list_node = new LinkedList();
p0 = GetMinYPoint();
LinkedListNode node = new LinkedListNode(nodes[0]);
list_node.AddFirst(node);
for (int i = 1; i < nodes.Count; i++)
{
int direct = IsClockDirection(p0, node.Value, nodes[i]);
if (direct == 1)
{
list_node.AddLast(nodes[i]);
node = list_node.Last;
//node.Value = nodes[i];
}
else if (direct == -10)
{
list_node.Last.Value = nodes[i];
//node = list_node.Last
//node.Value = nodes[i];
}
else if (direct == 10)
continue;
else if (direct == -1)
{
LinkedListNode temp = node.Previous;
while (temp != null && IsClockDirection(p0, temp.Value, nodes[i]) == -1)
{
temp = temp.Previous;
}
if (temp == null)
{
list_node.AddFirst(nodes[i]);
continue;
}
if (IsClockDirection(p0, temp.Value, nodes[i]) == -10)
temp.Value = nodes[i];
else if (IsClockDirection(p0, temp.Value, nodes[i]) == 10)
continue;
else
list_node.AddAfter(temp, nodes[i]);
}
}
sor_nodes = list_node.ToArray();
sortedNodes = new Stack();
sortedNodes.Push(p0);
sortedNodes.Push(sor_nodes[0]);
sortedNodes.Push(sor_nodes[1]);
for (int i = 2; i {
PointF p2 = sor_nodes[i];
PointF p1 = sortedNodes.Pop();
PointF p0_sec = sortedNodes.Pop();
sortedNodes.Push(p0_sec);
sortedNodes.Push(p1);
if (IsClockDirection1(p0_sec, p1, p2) == 1)
{
sortedNodes.Push(p2);
continue;
}
while (IsClockDirection1(p0_sec, p1, p2) != 1)
{
sortedNodes.Pop();
p1 = sortedNodes.Pop();
p0_sec = sortedNodes.Pop();
sortedNodes.Push(p0_sec);
sortedNodes.Push(p1);
}
sortedNodes.Push(p2);
}
}
private int IsClockDirection1(PointF p0, PointF p1, PointF p2)
{
PointF p0_p1 = new PointF(p1.X - p0.X, p1.Y - p0.Y);
PointF p0_p2 = new PointF(p2.X - p0.X, p2.Y - p0.Y);
return (p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) > 0 ? 1 : -1;
}
private PointF GetMinYPoint()
{
PointF succNode;
float miny=nodes.Min(r=>r.Y);
IEnumerable pminYs = nodes.Where(r => r.Y == miny);
PointF[] ps = pminYs.ToArray();
if (pminYs.Count() > 1)
{
succNode = pminYs.Single(r => r.X == pminYs.Min(t => t.X));
nodes.Remove(succNode);
return succNode;
}
else
{
nodes.Remove(ps[0]);
return ps[0];
}
}
private int IsClockDirection(PointF p0, PointF p1, PointF p2)
{
PointF p0_p1 = new PointF(p1.X-p0.X,p1.Y-p0.Y) ;
PointF p0_p2 = new PointF(p2.X - p0.X, p2.Y - p0.Y);
if ((p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) != 0)
return (p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) > 0 ? 1 : -1;
else
return DistanceOfNodes(p0, p1) > DistanceOfNodes(p0, p2) ? 10 : -10;
}
public Stack SortedNodes
{
get { return sortedNodes; }
}
}
{
private List
private Stack
public PointF[] sor_nodes;
public ConvexAogrithm(List
{
nodes = points;
}
private double DistanceOfNodes(PointF p0, PointF p1)
{
if (p0.IsEmpty || p1.IsEmpty)
return 0.0;
return Math.Sqrt((p1.X - p0.X) * (p1.X - p0.X) + (p1.Y - p0.Y) * (p1.Y - p0.Y));
}
public void GetNodesByAngle( out PointF p0)
{
LinkedList
p0 = GetMinYPoint();
LinkedListNode
list_node.AddFirst(node);
for (int i = 1; i < nodes.Count; i++)
{
int direct = IsClockDirection(p0, node.Value, nodes[i]);
if (direct == 1)
{
list_node.AddLast(nodes[i]);
node = list_node.Last;
//node.Value = nodes[i];
}
else if (direct == -10)
{
list_node.Last.Value = nodes[i];
//node = list_node.Last
//node.Value = nodes[i];
}
else if (direct == 10)
continue;
else if (direct == -1)
{
LinkedListNode
while (temp != null && IsClockDirection(p0, temp.Value, nodes[i]) == -1)
{
temp = temp.Previous;
}
if (temp == null)
{
list_node.AddFirst(nodes[i]);
continue;
}
if (IsClockDirection(p0, temp.Value, nodes[i]) == -10)
temp.Value = nodes[i];
else if (IsClockDirection(p0, temp.Value, nodes[i]) == 10)
continue;
else
list_node.AddAfter(temp, nodes[i]);
}
}
sor_nodes = list_node.ToArray();
sortedNodes = new Stack
sortedNodes.Push(p0);
sortedNodes.Push(sor_nodes[0]);
sortedNodes.Push(sor_nodes[1]);
for (int i = 2; i
PointF p2 = sor_nodes[i];
PointF p1 = sortedNodes.Pop();
PointF p0_sec = sortedNodes.Pop();
sortedNodes.Push(p0_sec);
sortedNodes.Push(p1);
if (IsClockDirection1(p0_sec, p1, p2) == 1)
{
sortedNodes.Push(p2);
continue;
}
while (IsClockDirection1(p0_sec, p1, p2) != 1)
{
sortedNodes.Pop();
p1 = sortedNodes.Pop();
p0_sec = sortedNodes.Pop();
sortedNodes.Push(p0_sec);
sortedNodes.Push(p1);
}
sortedNodes.Push(p2);
}
}
private int IsClockDirection1(PointF p0, PointF p1, PointF p2)
{
PointF p0_p1 = new PointF(p1.X - p0.X, p1.Y - p0.Y);
PointF p0_p2 = new PointF(p2.X - p0.X, p2.Y - p0.Y);
return (p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) > 0 ? 1 : -1;
}
private PointF GetMinYPoint()
{
PointF succNode;
float miny=nodes.Min(r=>r.Y);
IEnumerable
PointF[] ps = pminYs.ToArray();
if (pminYs.Count() > 1)
{
succNode = pminYs.Single(r => r.X == pminYs.Min(t => t.X));
nodes.Remove(succNode);
return succNode;
}
else
{
nodes.Remove(ps[0]);
return ps[0];
}
}
private int IsClockDirection(PointF p0, PointF p1, PointF p2)
{
PointF p0_p1 = new PointF(p1.X-p0.X,p1.Y-p0.Y) ;
PointF p0_p2 = new PointF(p2.X - p0.X, p2.Y - p0.Y);
if ((p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) != 0)
return (p0_p1.X * p0_p2.Y - p0_p2.X * p0_p1.Y) > 0 ? 1 : -1;
else
return DistanceOfNodes(p0, p1) > DistanceOfNodes(p0, p2) ? 10 : -10;
}
public Stack
{
get { return sortedNodes; }
}
}
界面部分,供测试使用:
public partial class Form1 : Form
{
private List
private Graphics g;
private Pen pen;
public Form1()
{
InitializeComponent();
g=this.panel1.CreateGraphics();
g.TranslateTransform(0f,this.panel1.Height);
g.ScaleTransform(1f,-1f);
pen = new Pen(Color.Blue);
}
private void button2_Click(object sender, EventArgs e)
{
g.Clear(panel1.BackColor);
nodes = new List
nodes.Clear();
Random rand = new Random();
Point p = new Point(); ;
for (int i = 0; i < 1000; i++)
{
p.X = rand.Next(10, panel1.Width - 9);
p.Y = rand.Next(10, panel1.Height - 9);
nodes.Add(p);
DrawCircle(p);
}
}
private void DrawCircle(Point p)
{
g.DrawEllipse(pen, p.X - 4, p.Y - 4, 8, 8);
g.FillEllipse(Brushes.Blue, p.X - 4, p.Y - 4, 8, 8);
}
private void button1_Click(object sender, EventArgs e)
{
ConvexAogrithm ca = new ConvexAogrithm(nodes);
PointF p;
ca.GetNodesByAngle(out p);
//PointF[] ps = ca.sor_nodes;
//float[] psangle=new float[ps.Length];
//for (int i = 0; i < psangle.Length; i++)
// psangle[i] = CalcAngle(p, ps[i]);
g.DrawEllipse(pen, p.X - 8, p.Y - 8, 16,16);
g.FillEllipse(Brushes.Blue, p.X - 8, p.Y - 8, 16, 16);
Stack
pen = new Pen(Color.Black, 2.0f);
g.SmoothingMode = SmoothingMode.HighQuality;
pen.LineJoin = LineJoin.Round;
g.DrawPolygon(pen, p_nodes.ToArray());
}
private float CalcAngle(PointF p1,PointF p2)
{
float angle = (float)(Math.Atan(Math.Abs(p2.Y - p1.Y + 0.0) / Math.Abs(p2.X - p1.X + 0.0)) * 180 / Math.PI);
if ((p2.Y - p1.Y + 0.0) / (p2.X - p1.X + 0.0) < 0)
angle = 180 - angle;
return angle;
}
}
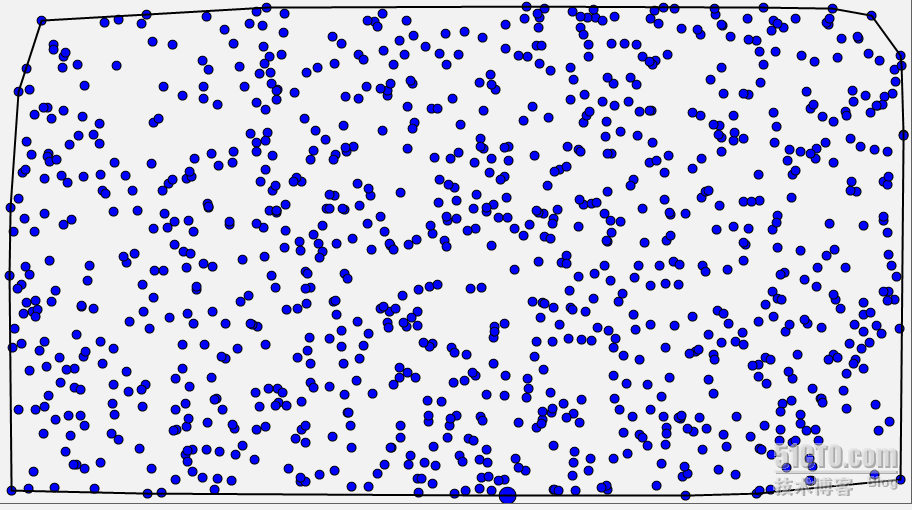
上面注释的为我当初测试排序极角的结果使用的,psangle是排序的结果,调试可看到角度从小到大。1000个点凸包如下(那个大圆点是P0,我为标记使用,无其他含义):
200个点的凸包如下: