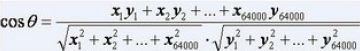很早之前看了几篇博文,只留下模糊印象 。这次是在学习人工智能的基础知识后再看,其中研究自然语言的方法从基于规则转变为基于统计,对我启发很大。 在面对一个复杂的问题时,一定要去想着把它转化成数学问题,而不是按照惯性思维去分析,只有转化成简单优雅的数学模型,才证明你的研究方向对了。电脑并不神秘,它其实只是傻瓜
全书内容多,本文只介绍三条主线:自然语言的统计模型、拼音输入法、搜索引擎。PS:不支持latex公式,让这篇文章写的很麻烦。
目录
1.文字和语言 vs 数字和信息
2.自然语言处理 - 从规则到统计
3.统计语言模型
4.中文分词
5.隐含马尔可夫模型
6.信息熵
7.牛人介绍: 贾里尼克(Jelinek,现代自然语言处理奠基者,将语音识别看作通信问题)
8.布尔代数,搜索引擎的索引
9.图论、网络爬虫
10.Page Rank,网页排名技术
11.TF-IDF,网页与查询相关性
12.有限状态机和动态规划-地图和本地搜索
13.牛人介绍:阿米特·辛格,
14.余弦定理和新闻分类
15.矩阵计算、文本处理中两个分类问题
16.信息指纹:哈希
17.密码学中的数学、信息论
18.搜索引擎反作弊
19.数学模型重要性
20.最大熵模型
21.拼音输入法的数学原理
22.牛人介绍:马库斯(Marcus),建立语料库。
23.布隆过滤器
24.贝叶斯网络
25.条件随机场和句法分析
26.牛人介绍:维特比,高通创办者,制定CDMA协议。
27.期望最大化算法
28.逻辑回归和搜索广告
29.Map Reduce
1. 自然语言处理,语音识别,机器翻译
1.1 基于规则的语言处理
早期学术界认为,要让机器完成翻译和语音识别这种人类才能做的事情,就必须先让计算机理解自然语言,而做到这点就要让机器有类似人类的智能。这个方法论被称为“鸟飞派”(通过观察鸟的飞行方式,采用仿生的思路造出飞机)。
那么怎么让机器理解自然语言呢?受传统语言学的影响,他们觉得要让机器做好两件事:分析句子语法和获取语义。分析句子语法就是按照语法把句子拆分,分清它的主语、谓语、宾语是什么,每个部分的词性是什么,用什么标点符号。而语义分析,就是弄清句子要表达的具体意思。语法规则很容易用计算机算法描述,这让人们觉得基于规则的方法是对的。但是这种方法很快就陷入困境,因为基于语法的分析器处理不了复杂句子,同时,词的多义性无法用规则表述,例如下面的例子:
The pen is in the box. 和 The box is in the pen.
第二句话让非英语母语的人很难理解,盒子怎么在钢笔里呢?其实在这里,pen是围栏的意思。这里pen是钢笔还是围栏,通过上下文已经不能解决,而需要常识,即钢笔可以放在盒子里,但是盒子比钢笔大,所以不能放在盒子里,于是pen在这里是围栏的意思,盒子可以放在围栏里。
1.2 基于统计的语言处理
贾里尼克(Jelinek)把语音识别问题当作通信问题,并用两个隐含马尔可夫模型(声学和语言模型)概括了语音识别,推动了基于统计的语言处理方法。
在语音识别中,计算机需要知道一个文字序列是否能构成一个大家理解而且有意义的句子。早期的做法是判断给出的句子是否合乎语法,由前文可知这条路走不通。贾里尼克从另外角度看这个问题:通过计算一个句子出现的概率大小来判断它的合理性,于是语音识别问题转换成计算概率问题,根据这个思路,贾里尼克建立了统计语言模型。
假定S表示某一个有意义的句子,由一连串特定顺序排列的词w1,w2,w3...组成。我们想知道S在文本中出现的可能性,计算S的概率P(S),根据条件概率公式:
其中P(w1)为w1出现的概率,P(w2|w1)为已知第一个词出现的条件下,第二个词出现的概率,以此类推。前面几个概率容易计算,但是后面的概率随着变量增多,变得不可计算。在这里需要应用马尔可夫假设来简化计算。马尔可夫假设假定当前状态只与前一个状态有关,即Wi出现的概率只同它前面的词有关Wi-1,于是上面的公式可以简化为:
接下来的问题是估算条件概率P(Wi|Wi-1),由条件概率公式得:
而估计联合概率P(Wi-1, Wi)和P(Wi-1)可以统计语料库得到,通过计算(Wi-1, Wi)这对词在语料库中前后相邻出现的次数C,以及Wi-1单独出现的次数,就可得到这些词或者二元组的相对频度。根据大数定理,只要统计量足够,相对频度就等于概率,于是
于是复杂的语序合理性问题,变成了简单的次数统计问题。
上式对应的统计语言模型是二元模型,实际应用中,google翻译用到四元模型。
1.3 中文分词
对于西方拼音语言来说,词之间有明确的分界符(空格),但是中、日、韩、泰等语言没有。因此,首先要对句子进行分词,才能做进一步自然语言处理。对一个句子正确的分词结果如下:
分词前:中国航天官员应邀到美国与太空总署官员开会。
分词后:中国/航天/官员/应邀/到/美国/与/太空/总署/官员/开会/。
最容易想到的分词方法是“查字典”,即把一个句子从左到右扫描一遍,遇到字典里有的词就标出来,遇到复合词就找最长匹配,遇到不认识的字串就分割成单字。这个方法能解决七八成的问题,但是遇到有二义性的分割就无能为力了,例如“发展中国家”,正确的分割是“发展-中-国家”,但是按照查字典法就会分成“发展-中国-家”。另外,并不是最长匹配都一定正确,例如“上海大学城书店”,正确的分割是“上海-大学城-书店”,而不是“上海大学-城-书店”。
按照前文的成功思路,依靠语法规则无法解决分词的二义性问题,还是得靠统计语言模型。
假设一个句子S有n种分词方法,利用前文的统计语言模型,分别计算出每种分词方法的概率,概率最大的即为最好的分词方法。因为穷举所有的分词方法计算量太大,所以可以把它看成是一个动态规划问题,并利用维特比算法快速找到最佳分词。具体应用时还要考虑分词的颗粒度。
2. 拼音输入法
2.1 拼音输入法中的数学
中文输入法经历了以自然音节编码输入,到偏旁笔画拆字输入,再回归自然音节输入的过程。输入法输入汉字的快慢取决于对汉字编码的平均长度,也就是击键次数乘以寻找这个键需要的时间。单纯地减少编码长度未必能提高输入速度,因为寻找一个键的时间会增长。
将汉字输入到计算机中,是将人能看懂的信息编码变成计算机约定的编码(Unicode或UTF-8)的过程。对汉字的编码分为两部分:对拼音的编码和消除(一音多字)歧义。键盘上可使用的是26个字母和10个数字键,最直接的方式是让26个字母对应拼音,用10个数字消除歧义性。只有当两个编码都缩短时,汉字的输入才能够变快。早期的输入法常常只注重第一部分而忽略第二部分,例如双拼输入法和五笔输入法。
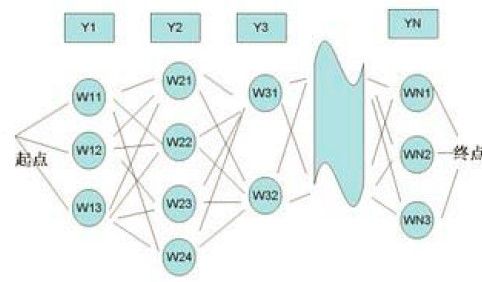
每一个拼音对应多个汉字,把一个拼音串对应的汉字由左向右连起来,就是一张有向图,如下图所示,y1,y2,y3...是输入的拼音串,W11,W12,W13是第一个音的候选汉字(后面的文字描述用W1代替),以此类推。从第一个字到最后一个字可以组成很多句子,每个句子对应图中的一条路径。
拼音输入法就是要根据上下文在给定的拼音条件下找到最优的句子,即求
(Arg是argument的缩写,Arg Max为获得最大值的信息串)
化简这个概率需要用到隐含马尔可夫模型(见2.2介绍),我们把拼音串看成能观察到的“显状态”,候选汉字看成“隐状态”,然后求在这个“显状态”下的“隐状态”概率。带入下文中的隐含马尔可夫模型公式(2.3),式(2.1)化简为:
化简连乘, 需要将等式两边取对数得
乘法变成了加法。我们定义两个词之间的距离
这样,寻找最大概率问题变成了寻找最短路径问题。
2.2 隐含马尔可夫模型
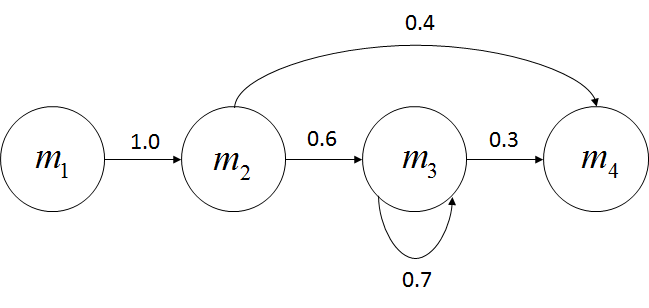
上文介绍过马尔可夫假设(研究随机过程中的一个假设),即在随机状态序列中,假设其中的一个状态只于前一个状态有关。如天气预报,假设今天的天气只与昨天有关,这样就能得到近似解:
符合这个假设的随机过程称为马尔可夫过程,也叫马尔可夫链。隐含马尔可夫模型是马尔可夫链的一个扩展:任意时刻t的状态St是不可见的,但在每个时刻会输出Ot, Ot仅和St相关,这叫独立输出假设,数学公式如下:
P(Ot|St)我们可以通过观察得到。
解决问题通常是通过已知求未知,我们要通过观察到$o_t$求出$s_t$的概率,即求
由条件概率公式可得:
因为观察到的状态O一旦产生就不会变了,所以它是一个可忽略的常数,上式可以化简为
因为
式(2.2)可以化简为
3.信息论:信息的度量和作用
3.1 信息熵
香农在他的论文“通信的数学原理”[想到牛顿的“自然哲学与数学原理”],提出了信息熵(shang),把信息和数字联系起来,解决了信息的度量,并量化出信息的作用。
一条信息的信息量和它的不确定性正相关,信息熵约等于不确定性的多少。香农给出的信息熵公式为
P(x)为x的概率分布。
信息熵的公式为什么取负数?因为概率小于1,小数求得的对数是负数,给整个公式加上负号,最终的结果为正。
下面举例说明信息熵公式为什么会用到log和概率。
猜中世界杯冠军需要多少次?
足球世界杯共32个球队,给他们编号1-32号,第一次猜冠军是否在1-16号之中,如果对了就会接着猜是否在1-8号,如果错了就知道冠军在9-16号,第三次猜是否在9-12号,这样只需要5次就能猜中,log32 = 5。这里采用的是折半查找,所以取对数。
但实际情况不需要猜5次,因为球队有强弱,可以先把夺冠热门分一组,剩下的分一组,问冠军是否在热门组中,再继续这个过程,按照夺冠概率对剩下的球队分组。引入概率就会让查找数更少,也就是不确定性更小,信息熵更小。可以计算,当每支球队夺冠概率相等时(1/32),信息熵的结果为5。
3.2 条件墒:
假定X和Y是两个随机变量,X是我们要了解的,已知X的随机分布P(X),于是X的熵为:
假定我们还知道Y的一些情况,包括它和X一起出现的概率,即联合概率分布,以及在Y取不同值前提下X的概率分布,即条件概率分布,于是在Y条件下X的条件熵为:
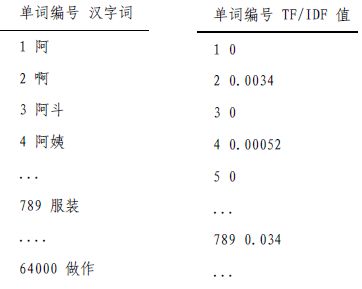
可证明H(X|Y) 信息之间的相关性如果度量呢? 香农提出了用互信息度量两个随机事件的相关性。例如,“好闷热”和“要下雨了”的互信息很高。 经过演算,可得到 只要有足够的语料库,P(x,y), P(x) 和P(y)是很容易计算的。 机器翻译中最难的两个问题之一是二义性,如Bush 既可以是总统布什,也可以是灌木丛,Kerry既可以是国务卿克里,也可以是小母牛。如何正确的翻译?一种思路是通过语法辨别,但效果不好; 另一种思路是用互信息,从大量文本中找出和总统布什一起出现的词语,如总统、美国、国会等,再用同样的方法找出和灌木丛一起出现的词,如土壤、植物等,有了这两组词,在翻译Bush时,看看上下文中哪类词更多就可以了。 相对熵(KL Divergence),衡量两个取值为正的函数的相似性: 结论: 在自然语言处理中,常用相对熵计算两个常用词在不同文本中的概率分布,看他们是否同义;或者根据两篇文章中不同词的分布,衡量它们的内容是否相等。利用相对熵,可以得到信息检索中最重要的概念:词频率-逆向文档频率(TF-IDF),在后面的搜索章节会对它详细介绍。 把整个互联网看作一张大图,每个网页就是图中的一个节点,超链接是连接节点的弧。通过网络爬虫,用图的遍历算法,就能自动地访问到每个网页并把它们存起来。 网络爬虫是这样工作:假定从一家门户网站的首页出发,先下载这个网页,再通过这个网页分析出里面包含的所有超链接,接下来访问并下载这些超链接指向的网页。让计算机不同地做下去,就能下载整个互联网。 还需要用一个记事本(哈希表)记录下载了哪些网页避免重复下载。 工程实现问题: 但是还要考虑网络通信的“握手”问题。网络爬虫每次访问网站服务器时,都要通过“握手”建立连接(TCP协议),如果采用广度优先,每个网站先轮流下载所有首页,再回过头来下载第二级网页,这样就要频繁的访问网站,增加“握手”耗时。 实际的网络爬虫是由成百上千台服务器组成的分布式系统,由调度系统决定网页下载的顺序,对于某个网站,一般是由特定的一台或几台服务器专门下载,这些服务器先下载完一个网站再进入下一个网站,这样可以减少握手次数(深度优先)。具体到每个网站,采用广度优先,先下载首页,再下载首页直接链接的网页。 页面分析和超链接(URL)提取 维护超链接哈希表 首先,这张哈希表会大到存不下来;其次,每台服务器下载前和下载后都要访问哈希表,于是哈希表服务器的通信就成了整个爬虫系统的瓶颈。解决办法是:明确分工,将某个区间的URL分给特定的几台服务器,避免所有服务器对同一个URL做判断;批量询问哈希表,减少通信次数,每次更新一大批哈希表的内容。 最简单的索引结构是用一个很长的二进制数表示一个关键字是否在每个网页中,有多少个网页就有多少位数,每一位对应一个网页,1代表相应的网页有这个关键字,0代表没有。比如关键字“原子能”对应的二进制数是0100 1000 1100 0001...表示(从左到右)第二、第五、第九、第十、第十六个网页包含这个关键字。假定关键字“应用”对应的二进制数是0010 1001 1000 0001...,那么要找到同时包含“原子能”和“应用”的网页时,只需要将这两个二进制数进行布尔AND运算,结果是0000 1000 0000 0001...表示第五和第十六个网页满足要求。 这个二进制数非常长,但是计算机做布尔运算非常快,现在最便宜的微机,在一个指令周期进行32位布尔运算,一秒钟十亿次以上。 为了保证对任何搜索都能提供相关网页,主要的搜索引擎都是对所有词进行索引,假如互联网上有100亿个有意义的网页,词汇表大小是30万,那么这个索引至少是100亿x30万=3000万亿。考虑到大多数的词只出现在一部分文本中,压缩比是100:1,也是30万亿的量级。为了网页排名方便,索引中还要存其他附加信息,如每个词出现的位置,次数等等。因此整个索引就变得非常大,需要通过分布式存储到不同服务器上(根据网页编号划分为很多小块,根据网页重要性建立重要索引和非重要索引)。 我们以查找包含“原子能的应用”网页举例,“原子能的应用”可以分成三个关键词:原子能、的、应用。凭直觉,我们认为包含这三个关键词较多的网页,比包含它们较少的网页相关。但这并不可取,因为这样的话,内容长的网页比内容短的网页占便宜,所以要根据网页长度对关键词的次数进行归一化,用关键词的次数,除以网页的总字数,这个商叫做“关键词的频率”或“单文本频率”(TF:Term Frequency)。比如,某个网页上有1000词,其中“原子能”“的”“应用”分别出现了2次、35次、5次,那么它们的词频就是0.002、0.035、0.005,将这三个数相加就是相应网页和查询“原子能的应用”的单文本频率。所以,度量网页和查询的相关性,一个简单的方法就是直接使用各个关键词在网页中出现的总频率。 但是这也有不准确的地方,例如上面的例子中,“的”占了总词频的80%以上,但是它对确定网页的主题几乎没什么用,我们叫这样的词为停止词(stop word),类似的还有“是”“和”等。 另外“应用”是很普通的词,而“原子能”是专业词,后者在相关性排名中比前者重要。因此需要给每个词给一个权重,权重的设定满足两个条件: 在信息检索中,使用最多的是“逆文本频率指数”(IDF:Inverse Document Frequency),公式为 (D是全部网页数,Dw为关键词w出现的网页个数)。最终确定查询相关性,是利用TF和IDF的加权求和。 (IDF其实是在特定条件下关键词概率分布的交叉熵) 这是拉里·佩奇和谢尔盖·布林发明的计算网页自身质量的数学模型,google凭借该算法,使搜索的相关性有了质的飞跃,圆满解决了以往搜索页中排序不好的问题。该算法的核心思想为:如果一个网页被很多其他网页所链接,说明它收到普遍的承认和信赖,那么它的排名就高。当然,在具体应用中还要加上权重,给排名高的网页链接更高的权重。这里有一个怪圈,计算搜索结果网页排名过程中需要用到网页本身的排名,这不是“先有鸡还是先有蛋的问题”吗? 谢尔盖·布林解决了这个问题,他把这个问题变成了一个二维矩阵问题,先假定所有网页排名相同(1/N),在根据这个初始值不断迭代排名,最后能收敛到真实排名。 google有新闻频道,里面的内容是由计算机聚合、整理并分类各网站内容。以前门户网站的内容是由编辑在读懂之后,再根据主题分类。但是计算机根本读不懂新闻,它只会计算,所以要让计算机分类新闻,首先就要把文字变成可计算的数字,再设计一个算法来计算任意两篇新闻的相似性。 计算一篇新闻中所有实词的TF-IDF值,再把这些值按照对应的实词在词汇表的位置依次排列,就得到一个向量。例如词汇表中有64000个词,其编号和词如左下表所示,在某一篇新闻中,这64000个词的TF-IDF值如右下表所示,这64000个数就组成了一个64000维的向量,我们就用这个向量代表这篇新闻,成为这篇新闻的特征向量。每篇新闻都有一个特征向量,向量中的每个数代表对应的词对这篇新闻主题的贡献。 同一类的新闻,一定某些主题词用的较多,两篇相似的新闻,它们的特征向量一定在某几个纬度的值比较大。如果两个向量的方向一致,就说明新闻的用词比例基本一致,我们采用余弦定理计算两个向量间的夹角: 新闻分类算法分为有目标和无目标:第一种是已知一些新闻类别的特征向量,拿它分别和所有待分类的新闻计算余弦相似性,并分到对应的类别中,这些已知的新闻类别特征向量既可以手工建立,也可以自动建立; 第二种是没有分好类的特征向量做参考,它采用自底向上的聚类方法,计算所有新闻两两之间的余弦相似性,把相似性大于一个阈值的新闻分作一个小类,再比较各小类之间的余弦相似性,就这样不断待在聚合,一直到某一类因为太大而导致里面的新闻相似性很小时停止。3.3 互信息
X与Y的互信息公式如下:![]()
3.4 相对熵/交叉熵
4. 搜索
4.1 获取网页:网络爬虫
搜索引擎要做到在有限的时间内,最多地爬下最重要的网页。显然各个网站最重要的是它的首页,那么就应该先下载所有网站的首页。如果把爬虫再扩大一点,就要继续下载首页直接链接的网页,因为这些网页是网站设计者自己认为相当重要的网页。在这个前提下,似乎应该采用广度优先。
早期的网页都是直接用HTML书写,URL以文本的形式放在网页中,前后有明显标识,很容易提取出来。但现在很多网页都是用脚本语言(如JavaScript)生成,URL不是直接可见的文本,所以网络爬虫要模拟浏览器运行网页后才能得到隐含的URL,但很多网页的脚本写的不规范,很难解析,这就导致这样的网页无法被搜索引擎收录。
在一台服务器上建立和维护一张哈希表并不是难事,但如果同时有成千上万台服务器一起下载网页,维护一张统一的哈希表就会遇到很多问题:4.2 网页检索:布尔代数
4.3 度量网页和查询的相关性:TF-IDF
![]()
4.4 搜索结果页排序:Page Rank算法
4.5 新闻分类:余弦定理