由于是毕业后转行的原因,所以本人在工作之前没有系统的学过数据结构、算法导论之类的课。说白了就是没有这样的底蕴,哈哈。所以这篇博客主要是写给自己看的,因为时间有限,本人写的内容估计远远不会有大家期待的那么详细,所以,可以此文可以选择性的忽略哦。
算法介绍:关于Boyer-Moore算法(后面简称BM算法)的概念网上一搜一大把。所以这里就不做具体阐述了。有疑问的建议参考阮一峰的这篇文章(此文文笔细腻且又通俗易懂):
阮一峰:字符串匹配的Boyer-Moore算法
算法精髓:这个字符串查找算法高效的原因在于当字符串不能完全匹配的时候可以一次性跳过多个字符。它不需要对被搜索的字符串中的字符进行逐一比较。那么,如何跳过呢?当然是利用模式字符串(pattern)和文本(text)在匹配过程中的已知信息跳过一些不必要的比较啦。上面推荐博文中的坏字符算法(bad-character)和好后缀算法(good-suffix )这两个启发式策略就是用于决定如何移动(shift)或者移动多少位的,此处就不细说啦。
完整算法:由于本文主要是用来助记的,不是循循善诱告诉你如何实现这个算法的。所以本人先贴出完整的代码(Java实现),然后再做进一步的代码分析吧。
public class BoyerMoore
{
public static void main(String[] args)
{
String text = "here is a simple example";
String pattern = "example";
BoyerMoore bm = new BoyerMoore();
bm.boyerMoore(pattern, text);
}
public void boyerMoore(String pattern, String text)
{
int m = pattern.length();
int n = text.length();
Map bmBc = new HashMap();
int[] bmGs = new int[m];
// proprocessing
preBmBc(pattern, m, bmBc);
preBmGs(pattern, m, bmGs);
// searching
int j = 0;
int i = 0;
int count = 0;
while (j <= n - m)
{
for (i = m - 1; i >= 0 && pattern.charAt(i) == text.charAt(i + j); i--)
{ // 用于计数
count++;
}
if (i < 0)
{
System.out.println("one position is:" + j);
j += bmGs[0];
}
else
{
j += Math.max(bmGs[i], getBmBc(String.valueOf(text.charAt(i + j)), bmBc, m) - m + 1 + i);
}
}
System.out.println("count:" + count);
}
private void preBmBc(String pattern, int patLength, Map bmBc)
{
System.out.println("bmbc start process...");
{
for (int i = patLength - 2; i >= 0; i--)
if (!bmBc.containsKey(String.valueOf(pattern.charAt(i))))
{
bmBc.put(String.valueOf(pattern.charAt(i)), (Integer) (patLength - i - 1));
}
}
}
private void preBmGs(String pattern, int patLength, int[] bmGs)
{
int i, j;
int[] suffix = new int[patLength];
suffix(pattern, patLength, suffix);
// 模式串中没有子串匹配上好后缀,也找不到一个最大前缀
for (i = 0; i < patLength; i++)
{
bmGs[i] = patLength;
}
// 模式串中没有子串匹配上好后缀,但找到一个最大前缀
j = 0;
for (i = patLength - 1; i >= 0; i--)
{
if (suffix[i] == i + 1)
{
for (; j < patLength - 1 - i; j++)
{
if (bmGs[j] == patLength)
{
bmGs[j] = patLength - 1 - i;
}
}
}
}
// 模式串中有子串匹配上好后缀
for (i = 0; i < patLength - 1; i++)
{
bmGs[patLength - 1 - suffix[i]] = patLength - 1 - i;
}
System.out.print("bmGs:");
for (i = 0; i < patLength; i++)
{
System.out.print(bmGs[i] + ",");
}
System.out.println();
}
private void suffix(String pattern, int patLength, int[] suffix)
{
suffix[patLength - 1] = patLength;
int q = 0;
for (int i = patLength - 2; i >= 0; i--)
{
q = i;
while (q >= 0 && pattern.charAt(q) == pattern.charAt(patLength - 1 - i + q))
{
q--;
}
suffix[i] = i - q;
}
}
private int getBmBc(String c, Map bmBc, int m)
{
// 如果在规则中则返回相应的值,否则返回pattern的长度
if (bmBc.containsKey(c))
{
return bmBc.get(c);
}
else
{
return m;
}
}
}
算法理论探讨与代码分析:
A1:坏字符算法理论探讨
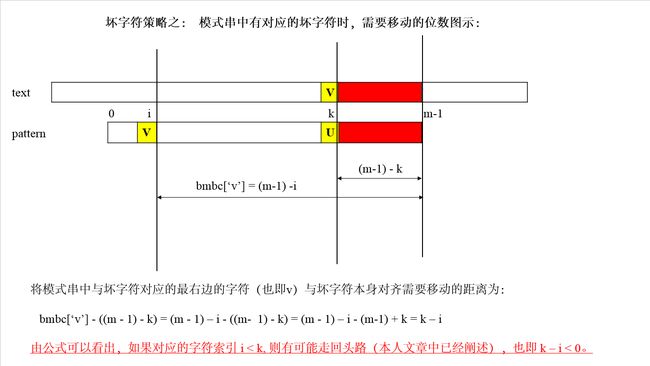
当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对,然后继续匹配。坏字符算法有两种情况。
1.模式串中有对应的坏字符时,让模式串中最靠右的对应字符与坏字符相对(由于是让坏字符与模式串中最靠右的对应字符对其,所以模式串有可能出现左移的情况,也即可能出现走回头路的情况,但若是走回头路,则移动距离就是负数了,肯定不是最大移动步数了)。
2.模式串中不存在坏字符,很好,直接右移整个模式串长度这么大步数。
A2:坏字符算法具体执行步骤:
BM算法子串比较失配时,按坏字符算法计算pattern需要右移的距离,要借助bmBc数组,而按好后缀算法计算pattern右移的距离则要借助bmGs数组。下面讲下怎么计算bmBc数组。
bmbc[]数组中,某个字符索引,比如bmbc[‘v’]表示字符v在模式串中最后一次出现的位置距离模式串串尾的长度。
计算坏字符数组bmBc[]:
这个计算应该很容易,似乎只需要bmBc[i] = m – 1 – i就行了,但这样是不对的,因为i位置处的字符可能在pattern中多处出现(如下图所示),而我们需要的是最右边的位置,这样就需要每次循环判断了,非常麻烦,性能差。这里有个小技巧,就是使用字符作为下标而不是位置数字作为下标。这样只需要遍历一遍即可,这貌似是空间换时间的做法,但如果是纯8位字符也只需要256个空间大小,而且对于大模式,可能本身长度就超过了256,所以这样做是值得的(这也是为什么数据越大,BM算法越高效的原因之一)。
如前所述,bmBc[]的计算分两种情况,与前一一对应。
Case1:字符在模式串中有出现,bmBc[‘v’]表示字符v在模式串中最后一次出现的位置,距离模式串串
尾的长度,如上图所示。
Case2:字符在模式串中没有出现,如模式串中没有字符v,则BmBc[‘v’] = strlen(pattern)。
将Case1写成伪代码也很简单:
void PreBmBc(char *pattern, int m, int bmBc[])
{
int i;
for(i = 0; i < 256; i++)
{
bmBc[i] = m;
}
for(i = 0; i < m - 1; i++)
{
bmBc[pattern[i]] = m - 1 - i;
}
}
当然在本人贴出来的完整代码中使用Map作为bmbc的存储结构,所以Case1的java表述如下:
private void preBmBc(String pattern, int patLength, Map bmBc)
{
System.out.println("bmbc start process...");
{
for (int i = patLength - 2; i >= 0; i--)
if (!bmBc.containsKey(String.valueOf(pattern.charAt(i))))
{
bmBc.put(String.valueOf(pattern.charAt(i)), (Integer) (patLength - i - 1));
}
}
}
那么,如何表述Case2呢,不可思议的简单,见下:可见使用Map作为bmbc存储容器在text字符不能穷尽256的情况下更加节省空间:
private int getBmBc(String c, Map bmBc, int m)
{
// 如果在规则中则返回相应的值,否则返回pattern的长度, 参数m恒等于pattern的长度
if (bmBc.containsKey(c))
{
return bmBc.get(c);
}
else
{
return m;
}
}
B1:好后缀算法理论探讨
如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀或后缀的部分, 那把下一个后缀或部分移动到当前后缀位置。假如说,pattern的后u个字符和text都已经匹配了,但是接下来的一个字符不匹配,我需要移动才能匹配。如果说后u个字符在pattern其他位置也出现过或部分出现,我们将pattern右移到前面的u个字符或部分和最后的u个字符或部分相同,如果说后u个字符在pattern其他位置完全没有出现,很好,直接右移整个pattern。这样,好后缀算法有三种情况:
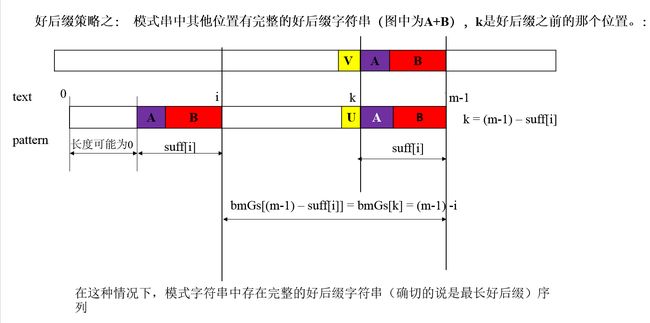
1.模式串中有子串和好后缀完全匹配,则将最靠右的那个子串移动到好后缀的位置继续进行匹配。
2.如果不存在和好后缀完全匹配的子串,则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。
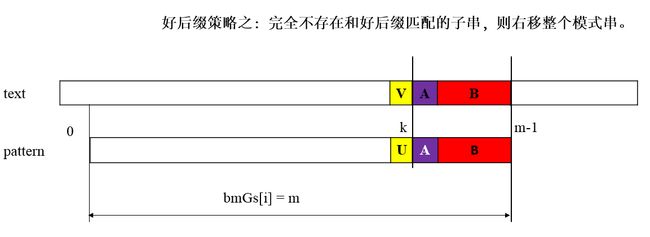
3.如果完全不存在和好后缀匹配的子串,则右移整个模式串。
综上可知,完整的BM算法的移动规则是:模式字符串每次比较的移动步长为 MAX(shift(好后缀),shift(坏字符)),即BM算法是每次向右移动模式串的距离是,按照好后缀算法和坏字符算法计算得到的最大值。坏字符算法的预处理数组是bmBc[],好后缀算法的预处理数组是bmGs[]。
B2:好后缀算法具体执行步骤:
这里bmGs[]的下标是数字而不是字符了,表示字符在pattern中位置。如前所述,bmGs数组的计算分三种情况,与前一一对应。假设图中好后缀长度用数组suff[]表示。
Case1:对应好后缀算法case1,如下图,K是好后缀之前的那个位置。
Case2:对应好后缀算法case2:如下图所示:
Case3:对应与好后缀算法case3,bmGs[i] = strlen(pattern)= m
根据上面的图示,给出的代码如下:
private void preBmGs(String pattern, int patLength, int[] bmGs)
{
int i, j;
int[] suffix = new int[patLength];
suffix(pattern, patLength, suffix);
// 先全部赋值为m,包含Case3
for (i = 0; i < patLength; i++)
{
bmGs[i] = patLength;
}
// Case2
j = 0;
for (i = patLength - 1; i >= 0; i--)
{
if (suffix[i] == i + 1)
{
for (; j < patLength - 1 - i; j++)
{
if (bmGs[j] == patLength)
{
bmGs[j] = patLength - 1 - i;
}
}
}
}
// 模式串中有最长好后缀,也即Case1
for (i = 0; i < patLength - 1; i++)
{
bmGs[patLength - 1 - suffix[i]] = patLength - 1 - i;
}
System.out.print("bmGs:");
for (i = 0; i < patLength; i++)
{
System.out.print(bmGs[i] + ",");
}
System.out.println();
}
上面的代码中用到了suffix数组,这个数组咋求呢?实际上suffix[i]就是求pattern中以i位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度。所以,其实现如下:
private void suffix(String pattern, int patLength, int[] suffix)
{
suffix[patLength - 1] = patLength;
int q = 0;
for (int i = patLength - 2; i >= 0; i--)
{
q = i;
while (q >= 0 && pattern.charAt(q) == pattern.charAt(patLength - 1 - i + q))
{
q--;
}
suffix[i] = i - q;
}
}
至此,BM算法的关键代码基本讲完了。完整代码在最开始也已经给出。在这里,本人想说的是,此处给出的代码还有许多可以优化和改进的地方,有兴趣的读者,可以参考下面这篇博文(用C#实现)哦:
grep之字符串搜索算法Boyer-Moore由浅入深(比KMP快3-5倍)