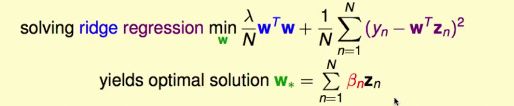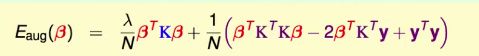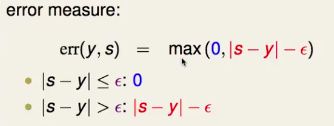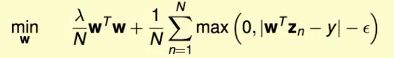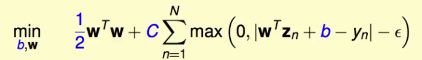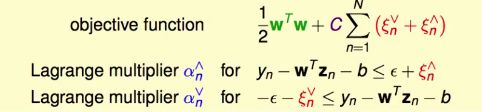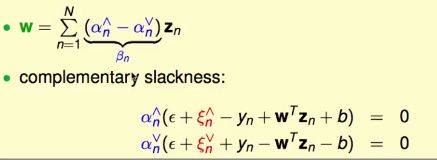本文参考整理了Coursera上由NTU的林轩田讲授的《机器学习技法》课程的第六章的内容,主要介绍了如何将kernel trick应用到ridge regression以及消除了LSSVM的稠密矩阵特性的基于tube error的SVR算法,总结归纳了我们之前五章所学到的所有的kernel模型。至此,我们的第一部分,利用kernel model解决巨量的特征的问题就讲述完毕了。文中的图片都是截取自在线课程的讲义。
欢迎到我的博客跟踪最新的内容变化。
如果有任何错误或者建议,欢迎指出,感激不尽!
--
本系列文章已发六章,前五章的地址如下:
- 一、线性SVM
- 二、SVM的对偶问题
- 三、Kernel SVM
- 四、Soft-Margin SVM
- 五、Kernel Logistic Regression
Kernel Ridge Regression
利用representer theorem可以把kernel ridge regression problem描述如下:
化简得
kernel ridge regression就是利用representer theorem,将kernel trick应用到ridge regression问题上。
怎么解β?
不难发现问题就是β的一个二次式,且问题是无条件最佳化问题,可以使用梯度为0求解,类似ridge regression可以直接得到analytic solution。
类比于单变量微积分求导法则,不难得到梯度的表达式如下:
若要▽E[aug](β)=0,一个解析解是使((λI+K)β-y)=0,即
矩阵的逆是否一定存在呢?
如果λ>0(对ridge regression一定满足λ>0),则一定存在逆,因为K是半正定的(Mercer's Condition),加上一个正的λI,一定是可逆的。
求逆需要时间O(N^3),且K矩阵是稠密矩阵。
linear versus kernel ridge regression
原来的linear ridge regression:
注意X矩阵是d*N维度的。
现在的kernel ridge regression:
linear的效率比较高,而kernel更加灵活flexible。
Support Vector Regression
之前讲过ridge regression也可以用作classification,那么kernel ridge regression当然也可以做classification,它的名称叫做least-squares SVM(LSSVM),即kernel ridge regression for classification。
Soft-Margin SVM versus Least-Squares SVM
两者边界类似,但是右边的support vectors数量明显更多,每一个都是SV。
SV太多==>预测越慢,β稠密,g很肥大
dense β:LSSVM、kernel LogReg
sparse α:standard SVM
目标:想让β也变得稀疏,就像标准SVM中的α矩阵一样。
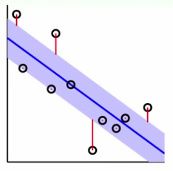
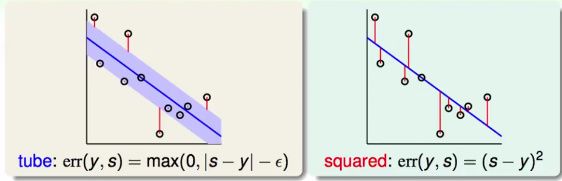
Tube Regression
我们允许一个中立区,当点落在蓝色区域内时,我们就不再考虑该点的错误。如果点在外面,就考虑错误点到中立区域的距离。
即错误衡量为:
通常叫该error measure为ε-insensitive error。(ε>0)
接下来,求解L2-regularized tube regression去得到稀疏的β。
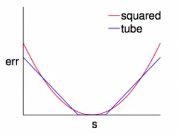
Tube error vs Squared error
当|s-y|比较小时,两者相似。但当差别比较大时,tube error受到的影响更小,比较不容易受到noise的影响而迁就。
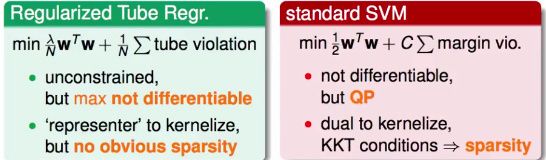
L2-Regularized Tube Regression
虽然是无约束问题,但是函数max不可微分,不好求解。
对比之前的标准SVM的求解方法,得到思路
模仿standard SVM形式:
改写系数、分离w0为b等微小改写操作
这还不是一个QP问题,因为条件中含有绝对值操作,并不是一个线性运算。
如何拆开绝对值?
把绝对值按照正负,拆成两个部分,用两个变量来记录,一个代表箭头往上的错误衡量、另一个代表箭头往下的错误衡量。当一个方向的tube violation不是0时,另一个方向的tube violation一定为0。
这是一个QP问题,有d~+1+2N个变量,有4N个条件。
这就是标准的Support Vector Regression(SVR) primal problem。
- 参数C:regularization和tube violation的折中。
- 参数ε:tube的竖直高度,对错误有多宽容。
SVR比SVM多一个参数ε可以选择。
下一步,通过转换SVR primal为SVR的dual问题,使用kernel trick,移除对Z空间维度d~的依赖。
SVR Dual
Lagrange Multipliers α↑ 和 α↓
对于条件ξn>=0的算子就不写了,因为类似于之前推导Soft Margin SVM的过程中,这样的multipliers β可以用C-α来表示。
推导过程类似以上所有SVM Dual的推导过程,min(max(L)) <==> max(min(L))、KKT条件等等。
这里直接给出几个KKT条件结果:
SVM Dual && SVR Dual
对偶问题有2N个变量,N个αn↑和N个αn↓。
SVR解的稀疏性
- 严格在tube里面,即|W’Zn+b-yn| < ε ==> εn↑ = εn↓ = 0 ==> αn↑ = αn↓ = 0 ==> βn = 0 ==>
- SVs(β!=0):刚好在tube边界上或者在外边。
这就说明了β是稀疏的。
Summary Of Kernel Models
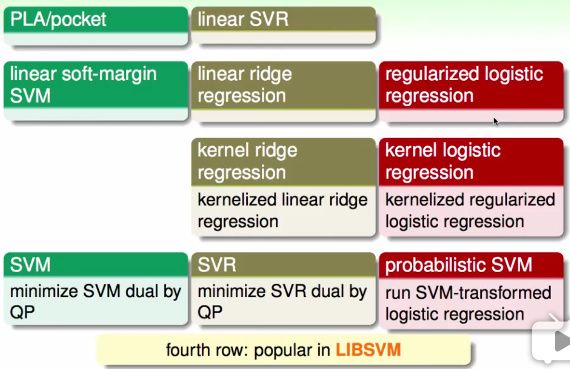
Map of Linear Models
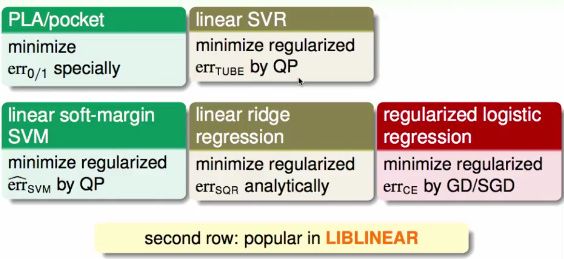
Map of Linear/Kernel Models
- 第一行中的方法由于表现比较差,在实践中比较少用。
- 第三行中的方法由于稠密矩阵β,在实践中也比较少用。
Kernel Models
可能的kernel:
- Polynomial
- Gaussian
- Your Design Kernel (with Mercer's Condition)
With great power comes great responsibility!!!
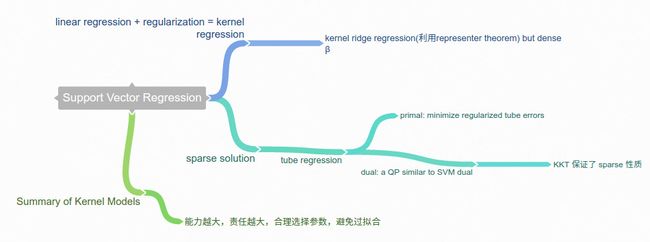
Mind Map Summary
这一章我们讲完了Support Vector Regression。至此,我们的第一大部分《embedding numerous features》也到此结束,如果你有很多很多features的时候,可以使用kernel的技巧,使用高维度的特征转换来做到这件事情。
下一章我们开始讲述如果我们有很多机器学习模型可用的时候,是否能把各种不同方法的优缺点结合起来,将不同的学习模型融合起来,得到一个powerful的综合模型呢?这一手段称为aggregation,我们将在后续几章中进行探讨,欢迎关注!