生存分析对应于一组统计方法,用于调查感兴趣事件发生所花费的时间。
生存分析被用于各种领域,例如:
癌症研究为患者生存时间分析,
“事件历史分析”的社会学
在工程的“故障时间分析”。
在癌症研究中,典型的研究问题如下:
某些临床特征对患者的生存有何影响?
个人三年存活的概率是多少?
各组患者的生存率有差异吗?
目标
本章的目的是描述生存分析的基本概念。在癌症研究中,大部分生存分析使用以下方法:
Kaplan-Meier绘制可视化生存曲线
对数秩检验比较两组或更多组的生存曲线
Cox比例风险回归来描述变量对生存的影响。Cox模型将在下一章讨论:Cox比例风险模型。
在这里,我们将首先解释生存分析的基本概念,包括:
如何生成和解释生存曲线,
以及如何量化和测试两组或更多组患者之间的生存差异。
然后,我们将继续使用Cox比例风险模型来描述多变量分析。
基本概念
在这里,我们从定义生存分析的基本术语开始,包括:
生存时间和事件
生存功能和危险功能
癌症研究中的生存时间和事件类型
有不同类型的事件,包括:
复发
级数
死亡
从“应对治疗”(完全缓解)到发生感兴趣事件的时间通常称为生存时间(或事件发生的时间)。
癌症研究中两个最重要的措施包括:i)死亡时间;和ii)无复发存活时间,其对应于治疗反应与疾病复发之间的时间。它也被称为无病生存时间和无事件生存时间。
如上所述,生存分析侧重于直到发生感兴趣事件(复发或死亡)的预期持续时间。然而,在研究时间段内,有些人可能不会观察到事件,从而产生所谓的审查意见。
审查可能出现在以下方面:
在研究时间内患者还没有经历过感兴趣的事件,如复发或死亡;
在研究期间患者失访;
患者经历不同的事件,使得进一步的随访变得不可能。
这种被称为正确审查的审查是在生存分析中处理的。
用两个相关的概率来描述生存数据:生存概率和危险概率。
的生存概率,也被称为幸存者功能小号(t)小号(Ť),是个体从时间起源(例如癌症的诊断)到指定的将来时间t存活的概率。
的危险,记ħ(吨)H(Ť),是在时间t观察的个人在那个时候发生事件的概率。
请注意,与没有发生事件的幸存者功能相比,危险功能着重于事件的发生。
Kaplan-Meier生存评估
Kaplan-Meier(KM)方法是一种非参数方法,用于估计观察到的生存时间的生存概率(Kaplan和Meier,1958)。
估计的概率(S(t)小号(Ť))是仅在每个事件发生时才改变值的阶跃函数。也可以计算生存概率的置信区间。
知识管理生存曲线是知识管理生存概率与时间的关系曲线,它提供了一个有用的数据总结,可以用来估计诸如中位生存时间之类的衡量指标。
R生存分析
安装并加载所需的R包
我们将使用两个R包:
生存计算生存分析
survminer的总结和可视化生存分析结果
安装软件包
install.packages(c("survival","survminer"))
加载包
library("survival")library("survminer")
示例数据集
我们将使用生存包中提供的肺癌数据。
data("lung")head(lung)
inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss1 3 306 2 74 1 1 90 100 1175 NA2 3 455 2 68 1 0 90 90 1225 153 3 1010 1 56 1 0 90 90 NA 154 5 210 2 57 1 1 90 60 1150 115 1 883 2 60 1 0 100 90 NA 06 12 1022 1 74 1 1 50 80 513 0
inst:机构代码
时间:以天为单位的生存时间
状态:审查状态1 =审查,2 =死亡
年龄:年龄
性别:男= 1女= 2
ph.ecog:ECOG表现评分(0 =好5 =死)
ph.karno:Karnofsky表现评分(bad = 0-好= 100)由医师评定
pat.karno:Karnofsky表现评分由患者评估
膳食:餐时消耗的卡路里
wt.loss:过去六个月的体重下降
计算生存曲线:survfit()
我们要按性别来计算生存概率。
功能survfit()[在存活包]可以被用来计算Kaplan-Meier存活估计。其主要论点包括:
使用函数Surv()创建的生存对象
和包含变量的数据集。
要计算生存曲线,请输入以下内容:
fit<-survfit(Surv(time,status)~sex,data=lung)print(fit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)n events median 0.95LCL 0.95UCLsex=1 138 112 270 212 310sex=2 90 53 426 348 550
默认情况下,函数print()显示生存曲线的简短摘要。它显示观察次数,事件数量,中位数生存和中位数的置信限。
如果要显示生存曲线的更完整摘要,请输入以下内容:
# Summary of survival curvessummary(fit)# Access to the sort summary tablesummary(fit)$table
访问由survfit()返回的值
函数survfit()返回一个变量列表,包括以下组件:
n:每条曲线的主题总数。
时间:曲线上的时间点。
n。风险:在时间t处于风险中的受试者数量
事件:在时间t发生的事件的数量。
传感器:在t时刻没有事件的退出风险集合的被审查主题的数量。
曲线的下限,上限:下限和上限置信界限。
地层:表示曲线估计的分层。如果地层不是NULL,则结果中有多条曲线。层次(一个因子)是曲线的标签。
可视化生存曲线
我们将使用函数ggsurvplot()(在SurvminerR软件包中)来生成两组受试者的生存曲线。
也可以显示:
使用参数conf.int = TRUE的幸存函数的95%置信限。
使用期权risk.table的风险个体的数量和/或百分比。risk.table允许的值包括:
指定是否显示风险表的TRUE或FALSE。默认值是FALSE。
“绝对”或“百分比”:分别显示风险对象的绝对数量和百分比。使用“abs_pct”来显示绝对数字和百分比。
Log-Rank测试的p值使用pval = TRUE比较组。
在使用参数surv.median.line的中值生存中的水平/垂直线。
情节可以进一步定制使用以下参数:
conf.int.style =“step”改变置信区间带的样式。
xlab更改x轴标签。
break.time.by = 200在时间间隔中将x轴断开200。
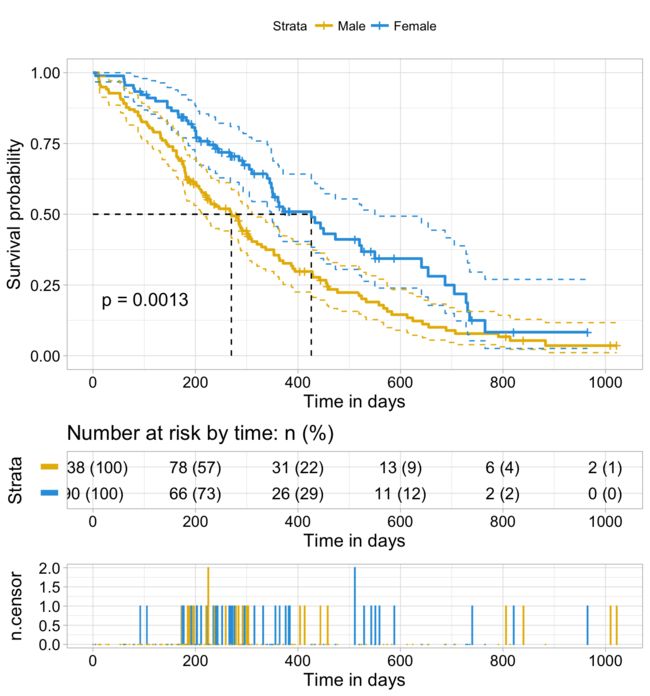
risk.table =“abs_pct”显示绝对数量和风险个体的百分比。
risk.table.y.text.col = TRUE和risk.table.y.text = FALSE在风险表的文本注释中提供条而不是名称。
ncensor.plot = TRUE绘制在时间t的审查主题的数量。正如Marcin Kosinski所建议的那样,这是对生存曲线的一个很好的附加反馈,所以人们可以认识到:生存曲线是怎样的,风险集合的数量是多少,风险集合的大小是多少?由事件或审查事件造成的?
legend.labs更改图例标签。
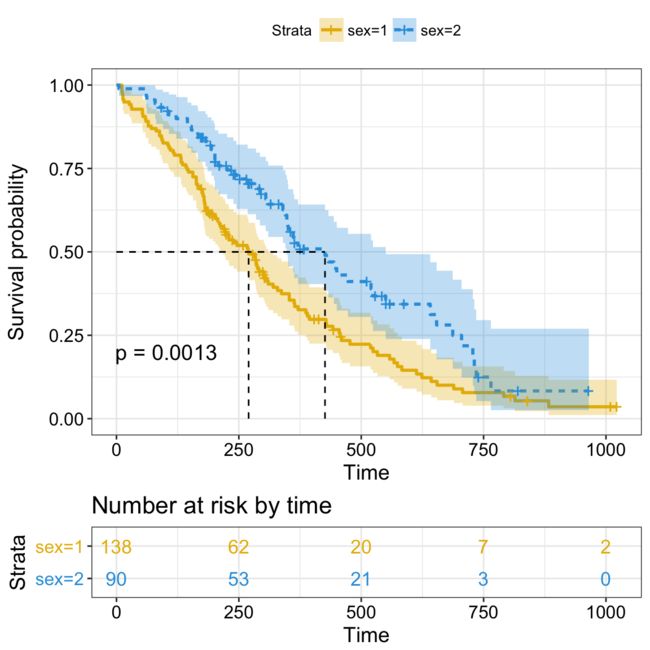
Kaplan-Meier图可以解释为:
横轴(x轴)表示以天为单位的时间,纵轴(y轴)表示存活的概率或者存活的人的比例。线条代表两组的生存曲线。曲线中的垂直下降表示一个事件。曲线上的垂直刻度标记表示此时患者被删除。
在零时间,生存概率是1.0(或100%的参与者是活着的)。
在时间250,性别= 1的生存概率约为0.55(或55%),在性别= 2时约为0.75(或75%)。
性别= 1的中位生存期约为270天,性别= 2的生存期为426天,表明性别= 2与性别= 1相比生存良好
每个组的中位生存时间可以使用下面的代码获得:
summary(fit)$table
每组的中位生存时间表示生存概率S(t)为0.5的时间。
性别= 1(男性组)的中位生存时间为270天,而性别= 2(女性)为426天。与男性相比,女性肺癌似乎有生存优势。但是,要评估这种差异是否具有统计显着性,需要进行正式的统计检验,这个问题将在下一节中讨论。
请注意,置信限度在曲线的尾部很宽,使得有意义的解释变得困难。这可以通过以下事实来解释:实际上,通常患者在随访结束时失去随访或存活。因此,在X轴追踪结束之前缩短阴谋可能是明智的(Pocock et al,2002)。
使用参数xlim可以缩短生存曲线,如下所示:
请注意,可以使用参数fun指定三个经常使用的转换:
“log”:生存者函数的日志转换,
“事件”:绘制累积事件(f(y)= 1-y)。这也被称为累计发病率,
“cumhaz”绘制累积危险函数(f(y)= - log(y))
例如,要绘制累积事件,请键入以下内容:
的累积性危险是常用来估计危险概率。它被定义为H(t)=-1og(survivalf)unction)=-log(S(t))H(Ť)=-升ØG(小号ü[Rv一世v一个升FüñCŤ一世Øñ)=-升ØG(小号(Ť))。累积危险(H(t)H(Ť))可以被解释为死亡率的累积力量。换句话说,如果事件是一个可重复的过程,它就相当于在时间t之前每个人所预期的事件的数量。
Kaplan-Meier生命表:生存曲线的总结
如上所述,您可以使用函数summary()来获得生存曲线的完整摘要:
summary(fit)
也可以使用函数surv_summary()[在survminer包中]获得生存曲线的总结。与默认的summary()函数相比,surv_summary()创建一个数据框,其中包含来自survfit结果的一个很好的总结。
res.sum<-surv_summary(fit)head(res.sum)
函数surv_summary()返回一个包含以下列的数据框:
时间:曲线有一个步骤的时间点。
n。风险:在t时刻有风险的科目数。
事件:在时间t发生的事件的数量。
n.censor:审查事件的数量。
幸存:估计生存概率。
std.err:生存的标准错误。
上:置信区间的上限
下限:置信区间的下限
地层:表示曲线估计的分层。层次(一个因子)是曲线的标签。
在生存曲线已经与一个或多个变量拟合的情况下,surv_summary对象包含表示变量的额外列。这使得有可能根据地层或某些因素的组合来面对ggsurvplot的输出。
surv_summary对象还有一个名为“table”的属性,其中包含关于生存曲线的信息,包括存活的置信区间的中位数,以及每个曲线中的主体总数和事件数量。要访问属性“表”,请输入:
attr(res.sum,"table")
Log-Rank检验比较生存曲线:survdiff()
对数秩检验是比较两条或更多条生存曲线的最广泛使用的方法。零假设是两组在生存期间没有差异。对数秩检验是一个非参数检验,不存在关于生存分布的假设。从本质上讲,对数秩检验将观察到的每组事件数量与假设假设为真(即生存曲线是否相同)所预期的数量进行比较。对数秩的统计近似地分布为卡方检验统计量。
存活包中的函数survdiff()可以用来计算比较两个或更多生存曲线的log-rank测试。
可以使用survdiff()如下:
surv_diff<-survdiff(Surv(time,status)~sex,data=lung)surv_diff
Call:survdiff(formula = Surv(time, status) ~ sex, data = lung)N Observed Expected (O-E)^2/E (O-E)^2/Vsex=1 138 112 91.6 4.55 10.3sex=2 90 53 73.4 5.68 10.3Chisq= 10.3 on 1 degrees of freedom, p= 0.00131
该函数返回一个组件列表,包括:
n:每组中的主题数量。
obs:每组中事件的加权观察数量。
exp:每组中事件的加权预期数量。
chisq:平等检验的统计量。
分层:可选地,每层中包含的主题的数量。
存活率差异的对数秩检验给出p = 0.0013的p值,表明性别组在存活方面差异显着。
适合复杂的生存曲线
在本节中,我们将使用多个因素的组合计算生存曲线。接下来,我们将面向ggsurvplot()的输出结合因素
require("survival")fit2<-survfit(Surv(time,status)~sex+rx+adhere,data=colon)
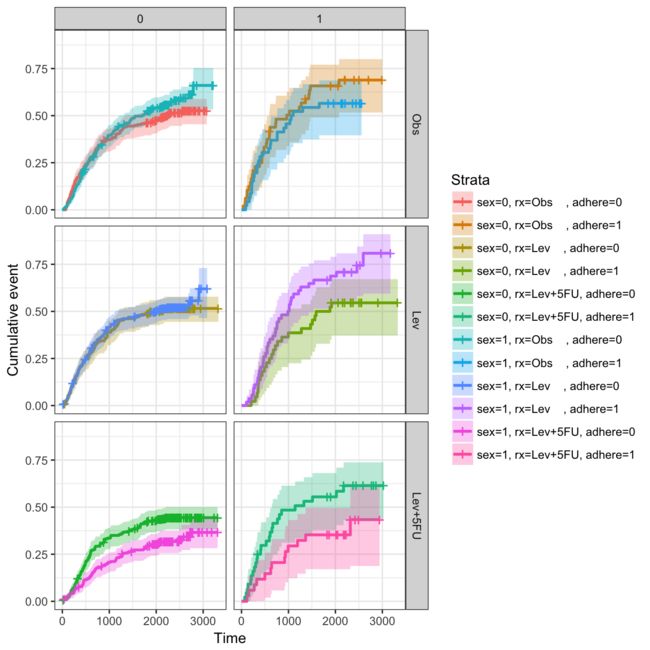
使用幸存者可视化输出。下面的图显示了性别变量根据rx&adhere的值生存的曲线。
# Plot survival curves by sex and facet by rx and adhereggsurv<-ggsurvplot(fit2,fun="event",conf.int=TRUE,ggtheme=theme_bw())ggsurv$plot+theme_bw()+theme(legend.position="right")+facet_grid(rx~adhere)
概要
生存分析是一组数据分析的统计方法,其中感兴趣的结果变量是事件发生之前的时间。
生存数据通常用两个相关函数来描述和建模:
幸存者函数表示个体从起源时间到时间t以后的某个时间存活的概率。通常采用Kaplan-Meier方法估算。logrank测试可以用来测试组之间的生存曲线之间的差异,例如治疗组。
危险函数给出了一次一个事件的瞬时潜能,并给出了直到那个时间的生存。它主要用作诊断工具或用于指定生存分析的数学模型。
在这篇文章中,我们演示了如何使用两个R软件包的组合来执行和可视化生存分析:生存(用于分析)和生存者(用于可视化)。
微信公众号