- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径
- (有向)无权图:BFS
- (有向)有权图:Dijkstra算法
- 多源最短路径问题:求任意两顶点间的最短路径
- 直接将单源最短路算法调用|V|遍
- Floyd算法
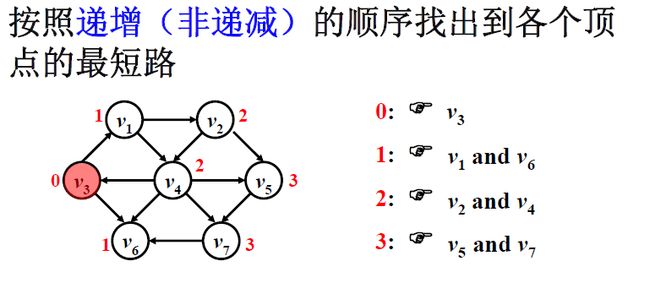
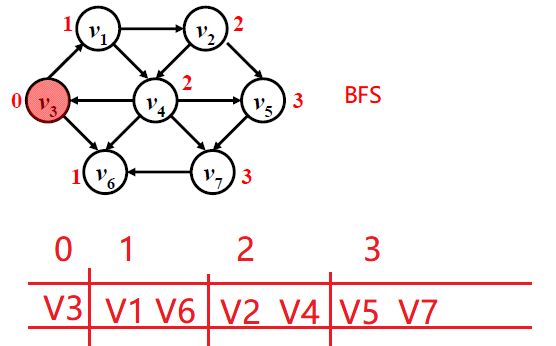
1.BFS算法求解单源无权图最短路径
1.1算法描述
广度优先搜索,开一个额外的数组存储每一个结点的访问状态,一层一层(取出队首元素,遍历所有相邻且未被访问的结点)的入队列,然后层数++
这里的额外数组就是dist[w],指的是从源点到顶点w的最短路径长度,初始化为-1,判断未访问即==-1,如果未访问且存在边G[v][w]则dist[w] = dist[v] +1 ;
path数组用于保存每一个顶点w的前驱顶点v,也即这条最短路径(s->w)必定是从(s->....->v->w),通过栈来逆序输出path[w] 、path[path[w]]....
更加详细的算法示例可以参考视频
1.2代码实现
#include
#include
#include
#include
#include
#define Init -1
#define MaxVertex 100
int path[MaxVertex]; // 存储路径,如果当前顶点v出队列,且存在顶点v->w的路径,则path[w] = v
int dist[MaxVertex]; // 存储路径长度,即从源顶点s到当前顶点w的最短路径dist[w]
int G[MaxVertex][MaxVertex]; // 图,采用邻接矩阵表示
int Ne; // 顶点数
int Nv; // 边
typedef int Vertex;
using namespace std;
void build(){
int v1,v2;
// 初始化点
cin>>Nv;
for(int i=1;i<=Nv;i++)
for(int j=1;j<=Nv;j++)
G[i][j] = 0;
// 初始化路径
for(int i=1;i<=Nv;i++)
path[i] = Init;
// 初始化路径长度
for(int i=1;i<=Nv;i++)
dist[i] = Init;
// 初始化边
cin>>Ne;
for(int i=0;i>v1>>v2;
G[v1][v2] = 1; // 有向图!
}
}
void Unweighted(Vertex v){
queue q;
dist[v] = 0; // 将自己的距离置 0 ,路径path[v]不变
Vertex w;
q.push(v);
while(!q.empty()){
w = q.front();
q.pop();
for(int i=1;i<=Nv;i++)
// 如果没被访问过,且连通
if(dist[i]==Init && G[w][i]){
dist[i] = dist[w]+1; // 是上一步的距离 + 1
path[i] = w; // w 是上一步要走路径的下一步路径
q.push(i);
}
}
}
// 获取路径
void getTail(Vertex v){
for(int i=1;i<=Nv;i++){
if(i==v)
continue;
stack s;
cout< 2.Dijkstra算法求解单源有权图最短路径
2.1算法描述
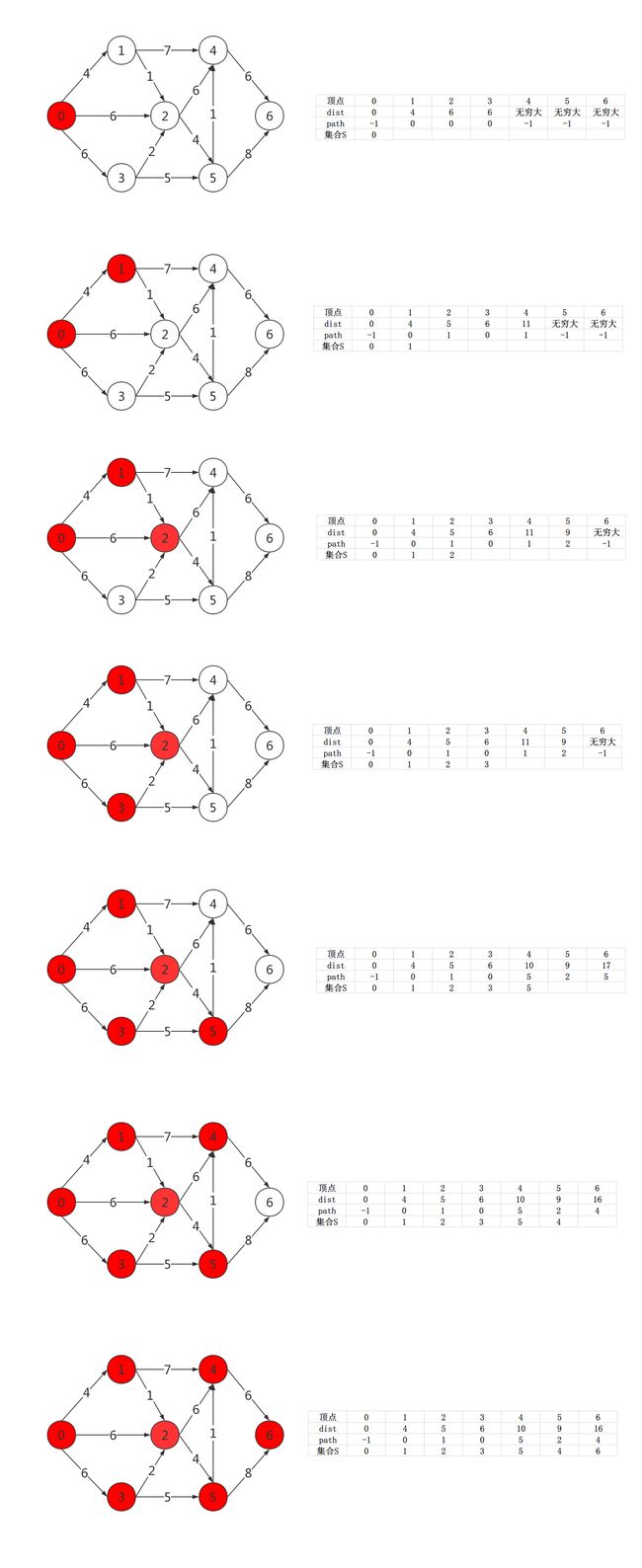
有权图的单源最短路算法可以使用Dijkstra算法实现,Dijkstra算法的基本思想是对图G(V,E)设置集合S,存放已被访问的顶点,然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。之后,令顶点u为中间点,优化所有起点s通过点u能够到达的邻接点v之间的最短路径。这样的操作执行n次,直到集合S已包含所有顶点。
算法的伪码描述如下:
void Dijkstra( Vertex s ) {
while (1) {
V = 未收录顶点中dist最小者;
if ( 这样的V不存在)
break;
collected[V] = true;
for ( V 的每个邻接点W )
if ( collected[W] == false )
if ( dist[V]+E < dist[W] ) {
dist[W] = dist[V] + E ;
path[W] = V;
}
}
} /* 不能解决有负边的情况*/ 引出了两个问题:
- 如何确定未收录顶点中dist最小者?
- 如何初始化dist[i]?
如何确定未收录顶点中dist最小者?
1.直接扫描所有未收录顶点,时间复杂度为– O( |V| ),总的时间复杂度为T = O( |V|^2 + |E| )对于稠密图效果好
2.将dist存在最小堆中,时间复杂度为– O( log|V| ),总的时间复杂度为T = O( |V| log|V| + |E| log|V| ) = O( |E| log|V| ),对于稀疏图效果好。
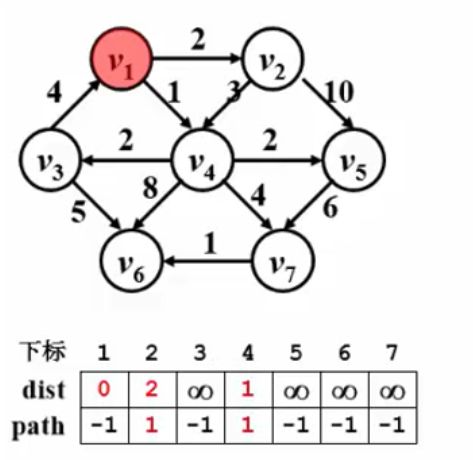
如何初始化dist[i]?
- 对于dist[0],也就是源点可以直接初始化为0
- 对于存在边
G[0][w],则dist[w]可以直接初始化为顶点s到顶点w的边权 - 其它的顶点w,初始化为infinity(无穷大)
- 初始状态,两个数组的初始化如上图所示
对于算法的详细示例可以参考视频
2.2代码实现
#include
#include
#define Inf 1000000
#define Init -1
#define MaxVertex 100
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int dist[MaxVertex]; // 距离
int path[MaxVertex]; // 路径
int collected[MaxVertex]; // 被收录集合
int Nv; // 顶点
int Ne; // 边
using namespace std;
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv;
// 初始化图
for(int i=1;i<=Nv;i++)
for(int j=1;j<=Nv;j++)
G[i][j] = 0;
// 初始化路径
for(int i=1;i<=Nv;i++)
path[i] = Init;
// 初始化距离
for(int i=0;i<=Nv;i++)
dist[i] = Inf;
// 初始化收录情况
for(int i=1;i<=Nv;i++)
collected[i] = false;
cin>>Ne;
// 初始化点
for(int i=0;i>v1>>v2>>w;
G[v1][v2] = w; // 有向图
}
}
// 初始化距离和路径信息
void crate(Vertex s){
dist[s] = 0;
collected[s] = true;
for(int i=1;i<=Nv;i++)
if(G[s][i]){
dist[i] = G[s][i];
path[i] = s;
}
}
// 查找未收录顶点中dist最小者
Vertex FindMin(Vertex s){
int min = 0; // 之前特地把 dist[0] 初始化为正无穷
for(Vertex i=1;i<=Nv;i++)
if(i != s && dist[i] < dist[min] && !collected[i])
min = i;
return min;
}
void Dijkstra(Vertex s){
crate(s);
while(true){
Vertex V = FindMin(s); // 找到
if(!V)
break;
collected[V] = true; //收录
for(Vertex W=1;W<=Nv;W++)
if(!collected[W] && G[V][W]){ // 如果未被收录
if(dist[V] + G[V][W] < dist[W]){
dist[W] = G[V][W] + dist[V];
path[W] = V;
}
}
}
}
void output(){
for(int i=1;i<=Nv;i++)
cout< 3.Floyd算法求解多源最短路径算法
#include
#include
#define INF 1000000
#define MaxVertex 100
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int dist[MaxVertex][MaxVertex]; // 距离
int path[MaxVertex][MaxVertex]; // 路径
int Nv; // 顶点
int Ne; // 边
using namespace std;
// 初始化图信息
void build(){
Vertex v1,v2;
int w;
cin>>Nv;
// 初始化图
for(int i=1;i<=Nv;i++)
for(int j=1;j<=Nv;j++)
G[i][j] = INF;
cin>>Ne;
// 初始化点
for(int i=0;i>v1>>v2>>w;
G[v1][v2] = w;
G[v2][v1] = w;
}
}
void Floyd(){
for(Vertex i=1;i<=Nv;i++)
for(Vertex j=1;j<=Nv;j++){
dist[i][j] = G[i][j];
path[i][j] = -1;
}
for(Vertex k=1;k<=Nv;k++)
for(Vertex i=1;i<=Nv;i++)
for(Vertex j=1;j<=Nv;j++)
if(dist[i][k] + dist[k][j] < dist[i][j]){
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = k;
}
}
void output(){
for(Vertex i=1;i<=Nv;i++){
for(Vertex j=1;j<=Nv;j++)
cout< 更多详细的算法描述请参考视频
以及文章