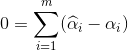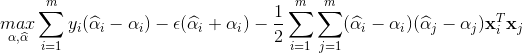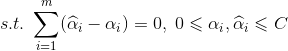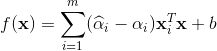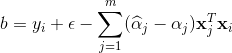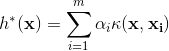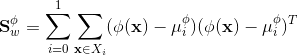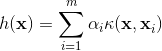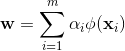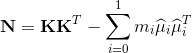《机器学习》西瓜书学习笔记（四）

上一篇笔记在这里：《机器学习》西瓜书学习笔记（三）

---

第六章 支持向量机

6.1 间隔与支持向量

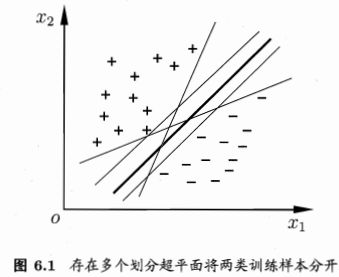
给定训练样本集D={(x₁,y₁),(x₂,y₂),...,(x_m,y_m)}，y_i∈{-1,+1}，分类学习就是基于训练集D在样本空间中找到一个划分超平面，将不同类别的样本分开。

直观上看，“最中间”的划分的鲁棒性最好。

在样本空间中，划分超平面可通过如下线性方程来描述：

其中w为法向量，决定了超平面的方向；b是位移项，决定了超平面和原点之间的距离。点x到该超平面的距离是：

这样的话，分类标准就是

支持向量和间隔

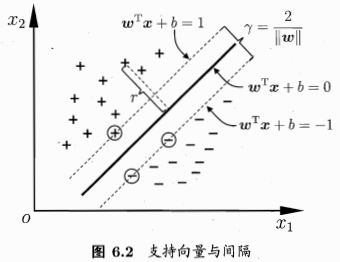
我们要做的就是找到“最大间隔”的划分超平面，即最小化||w||²，于是可重写为

这就是支持向量机（Support Vector Machine，简称SVM）的基本型。

6.2 对偶问题

对上面两个式子我们可以使用拉格朗日乘数法，对上式的每条约束添加拉格朗日乘子α_i>=0，则该问题的拉格朗日函数可写为

其中α=(α₁;α₂;...;α_m)，令L(w,b,α)对w和b的偏导为零可得

消去w和b，并考虑约束，可得对偶问题

解出α后，求出w与b即可得模型

从对偶问题解出的α_i是拉格朗日乘子，直接对应训练样本(x_i,y_i)。由于有不等式约束，因此上述过程需满足KKT（Karush-Kuhn-Tucker）条件，即要求

SMO（Sequential Minimal Optimization）算法：
基本思路：先固定α_i之外的所有参数，然后求α_i上的极值。由于α_？的和为0，若固定其他变量则可直接导出。所以选两个变量α_i和α_j. SMO算法不断执行以下两个步骤知道收敛：

• 选取一对需更新的变量α_i和α_j
• 固定α_i和α_j以外的参数，求解对偶问题获得更新后的α_i和α_j

注意到只需选取的α_i和α_j中有一个不满足KKT条件，目标函数就会在迭代后增大。直观来看，KKT条件违背的程度越大，则变量更新后可能导致的目标函数值增幅越大。于是，SMO先选取违背KKT条件程度最大的变量。第二个变量应选择一个使目标函数值增长最快的变量，但由于比较各变量所对应的目标函数值的复杂度变高，因此SMO采取一种启发式：使选取的两变量所对应样本之间的间隔最大。

如何确定偏移项b呢？注意到对任意向量(x_s,y_s)都有y
_sf(x_s)=1，即

其中S={i|α_i>0,i=1,2,...,m}为所有支持向量的下标集。理论上可选任意支持向量解得b，但现实我们适用所有支持向量求解的平均值

6.3 核函数

当样本线性不可分的时候，我们需要先做个映射Φ(x)，模型可表示为

其中w和b是模型参数，类似式(6,6)，有

其对偶问题是

直接算Φ( x _i) ^T和Φ( x _j)很困难，可以设想这样一个函数

将对偶问题重写为

求解后即可得到

其中κ(·,·)就是“核函数”，这一展式称为“支持向量模式”
定理6.1 （核函数）：
令X为输入空间，κ(·,·)是定义在X×X上的对称函数，则κ是核函数当且仅当对于任意数据D={x₁,x₂,...,x_m}，“核矩阵”K总是半正定的：

也就是说，只要对称函数所对应的核矩阵半正定，它就能作为核函数使用；反之，对于一个半正定核矩阵，总能找到一个与之对应的映射Φ。任何一个核函数隐式地定义了一个称为“再生核希尔伯特空间”（Reproducing Kernel Hilbert Space，RKHS）的特征空间。

核函数组合成新的核函数：

• 若κ₁和κ₂为核函数，则对于任意正数γ₁、γ₂，其线性组合
  
  
  也是核函数。
• 若κ₁和κ₂为核函数，则核函数的直积
  
  
  也是核函数。
• 若κ₁为核函数，则对于任意函数g(x)，
  
  也是核函数。

6.4软间隔与正则化

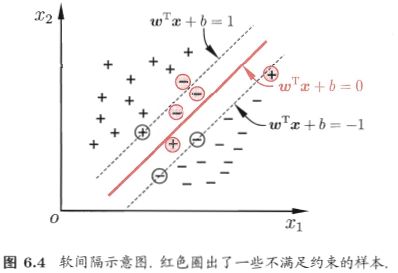
所谓“软间隔”，就是允许支持向量机在一些样本上出错。

软间隔允许某些样本不满足约束y_i(w^Tx_i+b)>=1。
所以我们在最大化间隔的同时，不满足约束的样本应尽可能的少，于是，优化目标为

6.29

其中，C>0是一个常数，l_0/1是“0/1损失函数”

但是l_0/1函数非凸非连续，所以人们用其他函数来代替l_0/1函数，称为“替代损失”：

hinge损失

指数损失

对率损失

若采用hinge损失，则式（6.29）则变为

引入“松弛变量”ξ_i>=0，可将上式重写为

使用拉格朗日乘数法

6.36

其中，α_i，μ_i是拉格朗日乘子。
对w，b，ξ_i偏导为0得

代入式（6.36）得到对偶问题

KKT要求是

我们可以将0/1损失函数换成别的替代损失函数以得到其他学习模型，可写成更一般的形式

其中Ω(f)称为“结构风险”，用于描述模型f的某些性质；第二项Σ^m_i=1l(f(x_i),y_i)称为“经验风险”，用于描述模型与训练数据的契合程度；C用于对二者进行折中。

6.5 支持向量回归（SVR）

我们考虑回归问题，给定样本D={(x₁,y₁),(x₂,y₂),...,(x_m,y_m))}

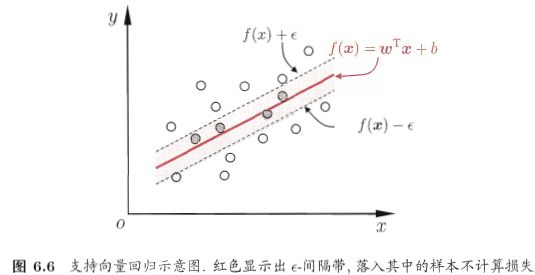
我们可以容忍f(x)与y之间最多有ε的偏差
SVR问题可形式化为

C为正则化常数，l_ε是ε-不敏感损失

引入松弛变量ξ_i和^ξ_i，重写为

引入拉格朗日乘子μ_i >= 0,^μ_i >= 0,α_i >= 0,^α_i >= 0，得到拉格朗日函数

将拉格朗日函数对w,b,ξ_i和^ξ_i求偏导置0可得

将以上四个式子代入拉格朗日函数，得到SVR的对偶问题

上述过程需满足KKT条件，即要求

SVR的解型为

由KKT条件可看出，对于每个样本(x_i,y_i)都有(C-α_i)ξ_i=0且α_i(f(x_i)-y_i-ε-ξ_i)=0.于是，在得到α_i后，若0<α_ii=0，进而有

因此，在解得α_i后，理论上来说可以任选0<α_ii

如果需要特征映射的时候w就变成

SVR可表示为

其中κ(x_i,x_j)=φ(x_i)^Tφ(x_j)为核函数。

6.6 核方法

表示定理：令H为核函数κ对应的再生核希尔伯特空间，||h||_H表示H空间中关于h的范数，对于任意单调递增函数Ω：[0,∞]→R和任意非负损失函数l：R^m→[0,∞]，优化问题

6.57

的解总可写为

表示定理对损失函数没有限制，对正则化项Ω仅要求单调递增，甚至不要求Ω是凸函数。

核线性判别分析（Kernelized Linear Discriminant Analysis，KLDA）：
先假设可通过某种映射φ：X→F将样本映射到一个特征空间F，然后在F中执行线性判别分析，以求得

6.59

KLDA的学习目标是

6.60

其中S_b^φ和S_w^φ分别为训练样本在特征空间F中的类间散度矩阵和类内散度矩阵。令X_i表示第i∈{0,1}类样本的集合，其样本数为m_i，总样本数m=m₀+m₁，第i类样本在特征空间F中的均值为

两个散度矩阵分别为

我们使用核函数方法，把J(w)作为式（6.57）中的损失函数l，在令Ω恒等于0，由表示定理，函数h(x)可写为

于是由式（6.59）得

令K∈R^m×m为核函数κ所对应的核矩阵，(K)_ij=κ(x_i,x_j)，令1_i∈{1,0}^m×1为第i类样本的指示向量，即1_i的第j个分量为1当且仅当x_j∈X_i，否则1_i的第j个分量为0.再令

式（6.60）等价为

其中α可由线性判别分析求解，进而可得投影函数h(x).

---

下一篇：《机器学习》西瓜书学习笔记（五）