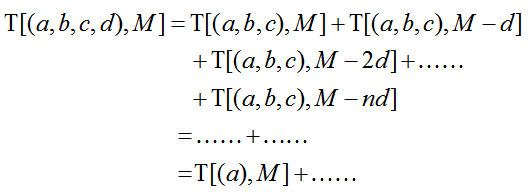前情参见:http://www.jianshu.com/p/558294dae12e
我叫欧木峰,是一名心理医生。
国外留学归来,我创办了辛境诊所。关小破是我的第一个患者,他是我高中同学子瑾的男朋友,患有幻听症。归国之前子瑾曾和我说起过她的男朋友,并寻求我的帮助。关小破,一个典型的理科IT男,天生有种不可理喻的执拗劲,对待任何事情都很专一。子瑾说她心底里很喜欢这种性格,她说可能是公司的加班压力大,生活节奏快才让关患上的幻听症,但是我并不这么认为,这件事也成为我回国办心理诊所的考量之一。
回国后,我和子瑾联系了几次,也特意叮嘱过她,不能让关知道我和她的同学关系。针对关小破的情况,我和子瑾制定了三个方案,最终选定哪一个,只有我见到本人才可以决定。
那天下午2点,我的诊所走进来一位男士,牛仔裤、T恤衫配上运动鞋,戴着大大的眼镜,长得很清秀,很阳光。
“我是关小坡,是瑾儿,是林子瑾介绍我来的”
“你好,我是欧木峰,这边坐,可乐、果汁还是咖啡”
“咖啡吧,这会有点困”
“你说一下你的大致情况吧”
“那我就和你说下今天上午的事情吧”
听完小破的自述,他的病因没有出乎我的意料。他是因为自我意识太过于强大,封闭了感官系统的外界连接,下意识的把自己的内心感受幻想为从外界得到的信息,从而产生幻听的感觉。简而言之就是脑洞太大。这种病如果任由其发展,就会完全陷入自己的意识里,不能脱离。
“你爱你女朋友吗”
“当然,如果没有他,这些日子我真不知道怎么度过”
“那你幻听过你女朋友的话吗”
“那倒没有,好像真没有过”
这更加验证了我的判断,因为他很爱子瑾,在接收来自子瑾的信息时,他强大的自我意识根本无法封闭住这连接,看来他真的很爱子瑾,也很爱推理。
“不好意思,我先出去一下打个电话,你在这等我一下啊,我这里有本数学谜题,你感兴趣可以看一下”
“子瑾,按方案三吧!我知道对你来说这个很难,但是这样是最好的。因为他从来没有幻听过你说的话”
“还来点咖啡吗”
“不用了,我看见数学题就来精神”
“我也很喜欢这些数学谜题,总想找到结果,前几天我看见一个有趣的问题,你听过换零钱吗,就是将面值100元的钱,换成面值1,2,5,10,20的钱,有多少种换法”
++++++一本正经的分割线+++++++
把100元兑换成1元,2元,5元,10元,20元,50元的零钱,共有多少种不同换法。
暴力依然可以解决问题,但是不优雅。因为需要多层for循环,并且移植性较差,对数值不同的问题需要更改程序。本文依然采用递归和动态规划的方法解决问题。
1,拆解子问题
下面以5元换成1,2,3元的零钱为例。T[(change),target]表示用零钱系列change组成target的所有方法。见下图:
其中T1可以看做用1和2元、不用3元组成5元的方法数;T2可以看做用1和2元、用1个3元组成5元的方法数;T6可看做用1元,用1个2元、不用3元组成3元的方法数;T9可看做用1元,用1个2元、1个3元组成0元的方法数。
状态转移表达式:
边界条件:
M-nd不得小于0,并且M-nd等于0时,表达式结果为1。如果表达式为T[(a),c],只有c除以a为整数,此表达式为1,否则为0。例如T[(2),5]=0,T[(2),6]=1。
1,递归的Python3实现
#根据边界条件,判断结果
def Solve(exlist,target):
#判断问题解
if target==0:
return 1
else:
if len(exlist)==1 and target%exlist[0]==0:
return 1
else:
return 0
#递归的方式,先将问题拆解子问题 ,然后在求解
def Dismantle(exlist):
if len(exlist[0][0])>1:
fu=[]
for ie in exlist:
for ji in range(int(ie[1]/ie[0][-1])+1):
fu.append([ie[0][0:-1],ie[1]-ji*ie[0][-1]])
return Dismantle(fu)
else:
return exlist
#计算结果
def Recursion(exlist,target):
structer=[[exlist,target]]
count=0
for jj in Dismantle(structer):#所有子问题的集合
if Solve(jj[0],jj[1])==1:#计算每一个子问题的结果
count+=Solve(jj[0],jj[1])
return count
print(Recursion([1,2,5,10,20,50],100))
结果:4562
2,动态规划的Python3实现
#动态规划
def DP_Com(exlist,num):
an=[1]+[0]*num
for i in exlist :
for j in range(i,num+1):
an[j]+=an[j-i]
return an[num]
print(Recursion([1,2,5,10,20,50],100))
结果:4562
++++++突如其来的分割线+++++++
关小坡这时给我说出了解题思路,但是事情并没有结束,他的眼睛直勾勾的盯着我,但是他根本没在看我。接下来的事情更加验证了我的推断。
++++++不能自已的分割线+++++++
有面值为1元、3元和5元的钱币若干张,如何用最少的钱币凑够11元,并列出组合方法。
子问题的状态转移表达式。
以下图为例:
动态规划的Python3实现
#记录
def DP_Min(exlist,target):
fan=[0]+[target]*target
record=['']*(target+1)
#存储最后一位
lic=[]
for i in exlist:
for j in range(i,target+1):
if fan[j-i]!=target:#如果等于target,说明之前没有数的结合可以达到这个数
fan[j]=min(fan[j-i]+1,fan[j])
#记录
if fan[j-i]+1<=fan[j]:
record[j]=record[j-i]+'%d*'%i
else:
record[j]=record[j]
if record[-1]!='':
lic.append(record[-1])
if len(lic)==0:
return '无解'
else:
return lic,fan[target]
#处理字符串
def Handle(exstr,num):
for i in set(exstr):
hu=i.split('*')
hu=list(filter(lambda x:x,hu))#去除掉split留下的空格
if len(hu)==num:
shuoming=''
for j in set(hu):
shuoming+='%s个%s '%(hu.count(j),j)
print(shuoming)
return 'Done'
ggg=DP_Min([1,3,5],11)
print(Handle(ggg[0],ggg[1]))
结果:最少为3。组合方法:2个5 1个1
++++++一剂猛药的分割线+++++++
未完待续