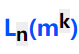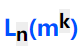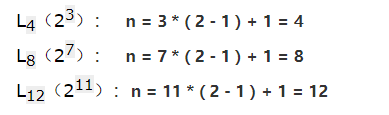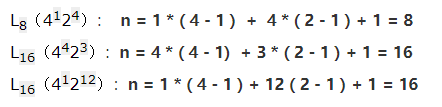关注 BeTester ,学习更多知识
让碎片成体系,让测试更专业
在科研和生产实践中,人们往往要做许多次实验来进行某项研究。实验结果一般由很多因素共同影响,因素的值不同产生不一样的试验结果。如果想把每个因素的每个值都要验证一遍,总验证次数就等于各因素的值的个数的乘积,而这个数往往超乎想象的巨大。
譬如,我们要研究是什么原因导致肥胖,经过一系列调查与分析,初步得出肥胖是由基因、睡眠时长、食物摄入量、运动量、摄入糖分比例、摄入脂肪比例6个因素影响。假设每个因素有3个取值,那要把每个因素的组合都验证一次,则要尝试 3x3x3x3x3x3 = 729 次。
为了减少实验次数,我们必须选出那些最有代表性的例子来完成尽可能多的覆盖验证。
1 正交试验概述
对于多输入条件组合类的测试方法,通常有两种方法,一种是正交试验法(Orthogonal Array),另一种是配对测试法(Pairwise或All-pairs)。这两种测试分析方法都是基于“缺陷都是单失效模式或双失效模式所发现的”,配对测试是完全基于两两组合所构成的测试用例,而正交试验则是在此基础上进行了简化,得到更加精细的测试用例。本文我们主要讲述正交试验测试分析法。
a. 单失效模式:失效是由单个因素引起的,只要针对独立参数进行测试即可发现问题。
b. 双失效模式:失效是由两个因素共同引起的,必须针对所有参数进行两两组合进行测试,才能确保发现问题。
c. 多失效模式:失效是由>3个因素共同引起的,只通过两两组合进行测试不能保证测试的充分性。
1.1 必知术语
因素:在试验中,影响试验结果的变量。
因素数:在试验中,影响试验结果的变量个数。
水平:因素所处的状态。
水平数:因素所包含的状态集合数量。
1.2 全面试验
全面试验,即全组合,也叫笛卡尔积,是对每个因素的每个水平互相搭配进行试验/验证。
假设,我们要完成某一款车的燃油消耗试验,经分析主要由车辆速度、车辆重量、车辆窗户开闭状态三个因素影响(因素数=3),并且每个因素都有3种状态,分别为高中低(水平数=3)。那么要进行全面试验的话,我们需要完成 3 x 3 x 3 = 27 次的试验。
1.3 正交试验
正交实验设计是研究多因素多水平的一种设计方法,它根据依据 Galois理论 从全面试验中挑选出部分具有代表性的水平组合进行试验,通过挑选部分有代表性的水平组合进行试验并对结果进行分析找出最优的水平组合。
正交试验让我们的工作带来了新的思考,有效提升工作效率。
同样,我们需要对汽车的燃油消耗进行试验,通过正交设计计算(后面介绍计算方法),我们可以得出只要 9 次就可以完成试验,工作效率提升2倍。
1.4 正交试验的意义
如果我们面对单因素或双因素进行试验的话,试验的设计、实施和分析都会比较简单。现实却是,我们总要面对3个或以上的因素,如果要进行全面试验,将会带来人力、时间、金钱的考验,甚至错过最佳的机会。
为了准确、合理减少不必要的试验成本,我们就可以使用正交试验。
1.5 正交试验的特点
分布均匀:任一列中,任一因素的水平(状态)出现的次数相同。
整齐可比:任两列中,任意一个水平组合出现的次数相同。
如果上述条件中的任一条不满足,则不再是正交表。
注:本节只讨论因素相互独立的正交试验法,因素间互相影响的在测试设计中无法使用。
2 正交试验使用方法
2.1 设计步骤
正交试验四步走:
(a)明确试验目的
(b)确定因素和水平
(c)选择合适正交表
(d)用例设计与编写
2.2 正交表
正交表是通过
来进行表达的,表示有 n 行的表格里,每一行有k个变量,每个变量的取值范围个数都是m。
从正交表的特性我们可以得知,并非所有 X x Y 的正交表都能够成为正交表,必须满足“均匀分布、整齐可比”才行。为此,我们需要一个已经存在的正交表提供我们选择,可参考下面内容:TS723_Designs 及 Taguchi Designs。
正交表的构造需要用到集合和概率学,如果正交表发生微小改变,其构造方法会产生也能产生巨大差异,甚至有些正交表其构造方法到目前还未解决。虽然简单的正交表可以自行推导出来,但建议采用现成的生成工具或参照先已公开的正交表模板进行设计以提高效率。
2.3 计算方法
L:正交表代号(没有实际意义)
n:正交表横行数(试验次数,即用例个数)
m: 因素水平数
k:正交表纵列数(最多能安排的因数个数)
用例数 n=k x (m-1)+1
2.4 计算实例
3 混合水平正交表
3.1 定义
混合水平正交表就是各因素水平数不完全相等的正交表。如
,表示有8行,5列(1+4),其中一列有4个水平,另外4列只有2个水平。
3.2 特性
任一列,不同数字出现次数相同
任两列,同行两个数字组成的各种不同的水平搭配出现的次数相同,但不同的两列所组成的水平搭配种类及出现次数不完全相同
3.3 计算实例
3.4 选择合适的正交表
当我们把因素和水平都找出来后,我们需要选择合适的正交表来完成试验。参考现有已经完成的正交表,我们需要选出与m^k形态 最接近的正交表 。
譬如,存在 m1 = 5, k1 = 5, m2 = 2, k2 = 1,根据计算公式:
n = 5x(5-1) + 1x(2-1) + 1= 22
我们发现没有 n = 22 的正交表,那如何选择合适自身的正交表呢?
(a)找出满足 n > 22 的正交表
(b)m > max(m1, m2) 即 m > max(5, 2) 且 k >= (k1+k2) = 5+1= 6
(c)选择 n 最小/最简单的正交表:
注:我们发现实际上 2^11 4^1 6^1 也符合,但是这个组合可能稍微复杂,我们可以选择更简单的正交表。
4 正交试验实例
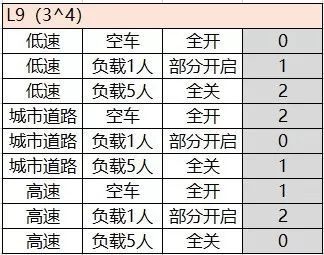
4.1 汽车燃油消耗
明确试验目的
对手机的拍照功能进行各种参数测试,使用正交试验对各个参数进行用例设计,提升测试效率。
确定因素和水平
车速:低速、城市道路、高速
车重:空车、负载一人、负载5人
车窗:全开、全关、部分开启
选择合适正交表
综上,存在 3个因素的水平数为3,所以 n = 3x(3-1) + 1= 7。
可选的正交表是:
把各个因素的水平与正交表进行一一映射。
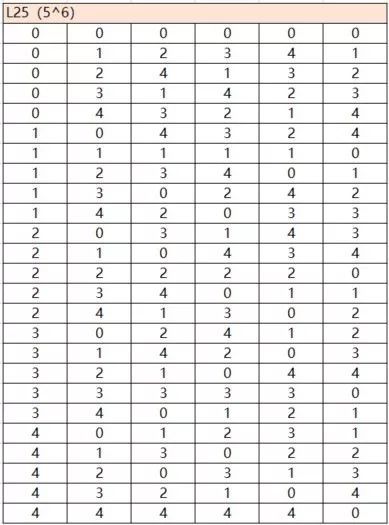
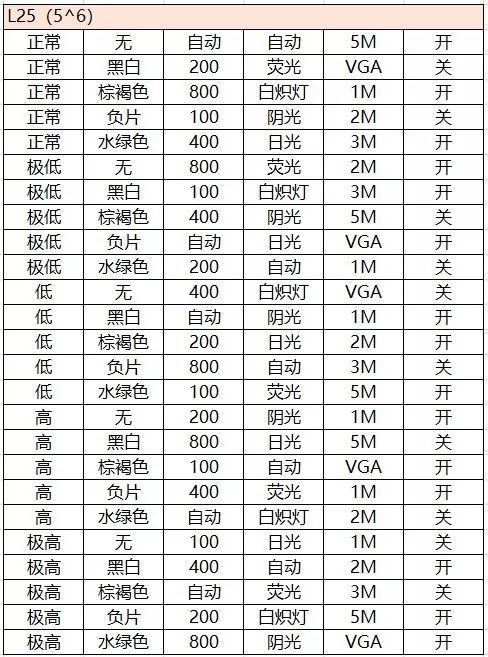
4.2 相机参数
明确试验目的
对手机的拍照功能进行各种参数测试,使用正交试验对各个参数进行用例设计,提升测试效率。
确定因素和水平
对比度:正常、极低、低、高、极高
色彩效果:无、黑白、棕褐色、负片、水绿色
感光度:自动、100、 200、 400、 800
白平衡:自动、白炽灯、日光、荧光、阴光
照片大小:5M、 3M、 2M、 1M、 VGA
闪光模式:开、关
选择合适正交表
综上,存在 5个因素的水平数为5, 1个因素的水平数为2,所以 n = 5x(5-1) + 1x(2-1) = 22 。
可选的正交表是:
把各个因素的水平与正交表进行一一映射。
注意:最后一列,水平不足时用其他数值替代,譬如选择偶数为开,奇数为关。
5 小结
在生活、工作、学习、生产等领域,我们都会经常使用正交试验,它为我们的工作效率带来了极大的提升。在测试领域里,测试是不可能穷尽的,并且缺陷具有群聚性,所以我们对正交试验的充分利用,能够给我们的测试工作带来极大的效率提升。
6 补充知识
6.1 N阶拉丁方
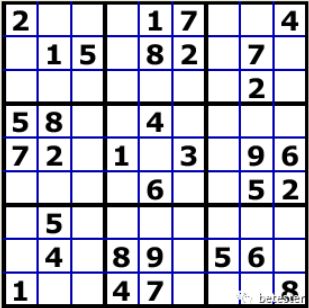
N阶拉丁方,也叫拉丁方阵,是一种 n x n 的方阵。在这种 n x n 的方阵里,恰好有 n 个不同的元素,每种不同的元素在同一行或同一列只出现一次。这不禁让我们想起自己曾经玩过的数学游戏,叫做 数独,在9x9的方格里,每行每列出现不一样的数字。
6.2 正交拉丁方
假设有 2 个 n阶拉丁方,如果把这两个拉丁方按照位置重新组合在一起,形成一个新的n阶拉丁方,并且恰好 组合而成的 n x n 元素各不相同,这种情况称之为两个拉丁方互相正交的拉丁方。
6.3 欧拉猜想(1782年)
有6个不同的师团,现在需要从6个师团中选取6位不同军衔的军官,共计36人。试问能否把这些军官排成6行6列的一个方阵,方阵中每行的6个军官恰好来自6个不同的师团,而且恰好不同军衔,每列也是来自6个不同军团的不同军衔。
欧拉猜想:不可能造出6阶正交拉丁方,同时对于10阶、14阶也不可能造出,一般来说,对于任何奇数的2倍(n=4k+2)都不可能造出。
直到 1966 年,才被 Lander和Parkin推翻,找出了 n = 5 的反例。但现在仍未找到 n> 5 的反例。
—— 更多文章 ——
黑盒测试设计专题:状态迁移
黑盒测试设计专题:判定表
黑盒测试设计专题:因果图
黑盒测试设计专题:边界值
黑盒测试设计专题:等价类
软件测试活动分类:按测试覆盖分类
软件测试活动分类:按测试方法分类
软件测试活动分类:按测试阶段分类
软件测试活动分类:按质量属性分类