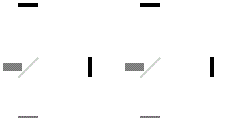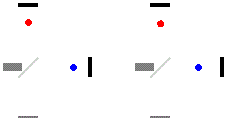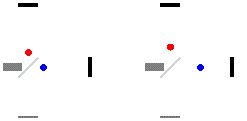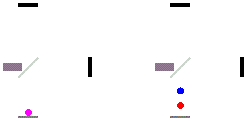我高中那会儿特别喜欢我们的地理老师(是地理,不是物理),按照现在的话来讲,就是他是一个段子手。
有一次课上,可能是说到白垩纪之类的,他说,如果你能站在距离地球两亿光年外的星球上用望远镜看地球,你就可以看到恐龙,这个就是因为相对论,时光倒流了。
这是我记忆中第一次听别人说起相对论,但其实这个说法和相对论压根就没什么关系。这就像是视屏聊天有延迟,并不代表你真的回到了几秒前的过去。
不过不管怎么样,我觉得任何一个人都不会对相对论这样的理论没有好奇心。你肯定或多或少听到过所谓的时间变慢、长度收缩之类的描述,并且还可能知道一个E等于mc平方的公式。但是我觉得除了理论的结论之外,提出理论的过程本身就已经够有意思的了,因此我将给你讲讲爱因斯坦到底是基于什么样的考虑想出狭义相对论这么一个匪夷所思的理论的。
一、伽利略相对性原理
我们先来做一个假想实验,时间回到1903年,那时麦克斯韦的电磁学理论已经建立,爱因斯坦刚刚入职成为瑞士专利局的助理鉴定员,从事电磁发明专利申请的技术鉴定工作,狭义相对论地提出还需要两年。
你一觉醒来发现身处一个房门紧闭,且没有窗户的封闭房间。你注意到房间里有一张桌子,桌子上放着一堆实验仪器,什么天平、计时器、弹力小球、弹簧秤之类的。你还发现房门紧锁,门上有两个分别标记着:“静止”和“匀速直线运动”的按钮,按钮旁边有个纸条威胁你道:”选择错误房间将爆炸!“。
你现在知道要做的就是用房间提供的仪器来检测到底房间是静止的还是匀速直线运动的,最后选择正确选项逃离这里。
你的主观感觉告诉你,你处于一个静止不动的房间中,但是你知道如果房间处于匀速直线运动的话,你同样感觉不到任何异样。
这时你想到了伽利略相对性原理:物理定律在一切惯性参考系中具有相同的形式,任何力学实验都不能区分静止和匀速运动的惯性参考系。
你想,妈呀!完了,这回出不去了。因为没办法通过力学实验来区分这个房间到底是匀速直线运动还是静止不动啊。
正当你沮丧的时候你突然发现仪器中有一些光学实验仪器,你灵机一动,想到有种叫以太的物质,它弥漫于宇宙之中。光的传播介质就是以太,以太是绝对不动的,如果房间相对于以太运动,测量房间各个方向的光速,看看是否不同,就可以知道房间是否在运动,以及朝哪个方向运动。
你为你的天才想法感到高兴,然后开始了如下实验:在房间的正中央同时向四面八方发射一束光,并且在上下四周的墙上装一面反射镜,哪面墙的光最先返回来,说明房间是在朝着这个方向运动,因为光速是相对于以太这个绝对静止的参考系的,房间朝这个方向运动了,光走的距离就短了,所以这个方向的光先反射回来了。
你心灵手巧,实验很快有了结果:各个方向的光都同时返回了。根据这个结果,你认为房间就是静止的,然后你把手放在了标记了”静止“的按钮上。房间有没有爆炸咱们待会再说,历史上真的就有人做过类似的实验。
二、迈克耳逊-莫雷实验
其实早在1887年的时候,就有一个叫迈克耳逊和一个叫莫雷的科学家把地球当成是运动的房子,做了测量各个方向光速的实验。
跟我们的封闭房子不同的是,当时已经知道地球以每秒30公里的速度绕太阳运动,也就是地球的公转。如果你把地球当成房子,那么就是已知房子正在高速运动,如果朝平行于公转方向和垂直于公转方向分别发射一束光,则预期结果就应该是朝着地球运动方向发射的光应该先返回,垂直地球运动的光后返回,如下图所示。
但实验显示出和左边图示一样的的结果:即两个方向的光同时到达。
前面提到本来是想证明以太存在,光就是以以太为介质传播的,垂直和平行两个方向的光速应该如右图所示才对。但现在实验结果和之前的预期不一样了,那要怎么解释呢?要么是实验做错了或者不精确,或者:
a. 根本就不存在以太,光速就是一个不依赖于参考系的绝对数;
b. 存在一种我们尚未理解的机制。
我们先说可能性b。
历史上一个叫洛伦兹的荷兰物理学家就觉得光的传播毕竟还是要有一个介质,实验结果其实说明不了以太不存在。迈克尔逊-莫雷实验之所以没有得到期望的结果,那是因为运动物体的长度会收缩,并且收缩只发生运动方向上,这样房间虽然在运动,但是由于尺度收缩了,光线走的距离短,还是同时反射回房间中央。并且洛伦兹在1904年还提出了一组公式,叫做洛伦兹变换,这个变换就定量描述了随着速度的变快,长度随之缩小,缩小到正好各个方向看不出差别。
洛伦兹的解释看起来挺不错,但是也有缺点:
首先,以太是没有直接观测到的,你必须假设以太要作为一个绝对参考系而存在;
第二是,因为以太存在于一个绝对静止的参考系中,绝对静止和匀速直线运动这两个参考系便有差别了,相对性原理从此就不成立了(相对性原理是说物理规律在静止和匀速直线运动参考系中是无区别的)。
现在再说可能性a。
缺点是它完全不符合我们的日常的经验:如果船以每秒3米的速度匀速直线运动,你以每秒1米的速度朝船头走去,那么你相对于海面的速度就是3+1=4(米/秒)。但是,对于光来说,你在船上朝船头发射一束速度为300000000米/秒的光,它相对于海面的速度却不是300000003米/秒,居然仍是300000000米/秒。
优点有两个:
一是相对性原理没有破坏,意思就是你在刚才那个封闭房间中死定了,因为无论力学实验还是电磁学、光学实验都没发区分到底你是在运动还是静止。这其实就是狭义相对性原理,他的完整表述就是:物理定律在一切惯性参考系中具有相同的形式。
二是不用假设目前观测不到的以太,不做多余的假设是一个优点。
你可能已经猜到了,爱因斯坦选择的就是这个可能性。不过你猜不到的是选择b中的洛伦兹变换和选择a并不矛盾。
三、伽利略变换与洛伦兹变换
爱因斯坦选择了可能性a,就是说相对性原理继续成立,并且要求光速在任意参考系中不变。
爱因斯坦于是把相对性原理和光速不变作为他的新理论的两个基本假设,且只有这两个假设,并由此推导出了洛伦兹变换。
哎,等等,你说洛伦兹变换不是洛伦兹提出的吗,怎么这里也可以得到?这里我们还得说说什么是伽利略变换与洛伦兹变换。
为了搞清楚什么是变换,我们先说参考系。你应该注意到了之前说的你在船上走,船在水上走正好就是两个参考系:你相对于船是一个,船相对于海是另一个。我们刚才还通过你相对于船的速度是1米/秒,船相对于海的速度是3米/秒计算出了你相对于海的速度是4米/秒。
那什么是变换呢?简单来讲,物体在一个参考系中的状态(位置、速度等)要通过一个数学变换,变换到另一个参考系中。例如对于速度来讲,简单相加就可以了。伽利略在他那个年代就总结出了这个规律,被称作伽利略变换。有了伽利略变换,物体的状态就可以从一个惯性坐标系转到另一个惯性坐标系。
但是,刚才你已经看到了,光速不变和伽利略变换是矛盾的。事实上整个麦克斯韦的电磁理论都不满足伽利略变换。
那如果我知道船上的电场强度或者磁场强度,如何转换到相对于大海这个参考系的电场强度或磁场强度呢?答案就是我们之前提到过的洛伦兹变换。
前面我们提到洛伦兹变换最早是洛伦兹在1904年提出用来解释迈克尔逊-莫雷实验的,后来又说通过相对性原理和光速不变两个基本假设可以直接推导出来。
那是不是意味着所有问题都解决了呢?
只要碰到力学问题,我们就用伽利略变换,碰到电磁学问题,我们就用洛伦兹变换,似乎所有问题都解决了。
但是爱因斯坦不满足于此,他认为所有的物理规律在惯性参考系中的变换都应该用洛伦兹变换而不是伽利略变换。
那么问题来了,伽利略变换用的好好的,都好几百年了,也没见有什么问题,怎么就突然给推翻了呢,推翻了之后你又怎么解释力学现象呢?
物理理论的进步不是简单的推翻旧的建立新的,爱因斯坦发现伽利略变换其实是洛伦兹变换的低速近似,其中的低速是相对于光速而言的。
我给你举个例子看看低速的近似到底精确度怎么样。比如还是我们在船上行走的例子:船相对于水面的速度是3米/秒,你朝船头走去,相对于船的速度是1米/秒,按照伽利略变换,你相对于海面的速度就是3+1=4(米/秒)。
但是按照洛伦兹变换,你相对于海面的速度是:4.00000000000000003米/秒(计算器已经计算不了这样的数了,我不得不写一个程序来计算光速这么大的数的平方并得到以上结果)。
这么说来,伽利略变换在低速情况下已经很好地描述了这个世界。
我们再看看高速情况下会发生什么。如果你能以0.9倍的光速朝船头跑动,同时船相对于海面的速度也是0.9倍光速,按照伽利略变换,那么你相对于海面的速度就是0.9+0.9=1.8倍光速。
但是按照洛伦兹变换,你相对于海面的速度是0.947倍的光速,你相对于海面的速度确实比相对船要快,但没有超光速,只是更加接近光速了。
事实上,根据洛伦兹变换的数学表达式,可以证明变换后的速度无论如何也不可能超过光速。
四、狭义相对论
刚才我们说到爱因斯坦不满足于电磁学和力学分别遵守两套变换,认为一切力学的规律也应该遵从洛伦兹变换,并且伽利略变换只是一个低速近似。
那么从洛伦兹变换出发,肯定可以得到一套升级版的力学理论,牛顿力学是这套力学理论的低速近似。
狭义相对论就是这样的理论。狭义相对论统一了牛顿力学和麦克斯韦的电磁理论,他们都遵守相对性原理(现在叫狭义相对性原理),满足洛伦兹变换。
由于洛伦兹变换中不是空间、时间各变各的,而是交织在一起的,因此狭义相对论才会得出大家可能已经听过的钟慢效应和尺缩效应的。
至此,整个发现狭义相对论的过程就讲完了。最后,我再给你总结一下整体的逻辑思路:
在电磁理论问世之前,牛顿的经典力学满足相对性原理,即物理定律在任意一个惯性参考系中都是一样的,并且物体的状态在各惯性参考系中的变换叫做伽利略变换。
随着麦克斯韦电磁理论的发展,波动方程中出现了光速。当时人们认为任何波动都要通过介质传播,并假设以太就是光传播的介质,它弥漫在全宇宙,方程中的c就是光相对于以太传播的速度。
但是这个假设有一个问题,就是如果真的存在这样一种以太,那么就必须推翻相对性原理,因为以太就是一个和其他惯性参考系都不同的特殊参考系。如果光的速度是相对于这个参考系的,在其他参考系中的电磁定律的形式肯定会不一样。
为了证明以太真的存在,迈克耳逊和莫雷两人用一束平行于地球公转方向的光和一束垂直于地球运动方向的光做了实验,但是实验结果和预期不同,没有证明以太确实存在。
1904年,荷兰物理学家洛伦兹为认为光的传播还是应该有个介质,为了解释迈克尔逊-莫雷实验,他提出了以他名字命名的洛伦兹变换。
这个变换有别于伽利略变换,它表明运动物体的长度会收缩,并且收缩只发生运动方向上,这样就解释了为什么测量不到垂直和平行方向上的差别,因为平行方向的收缩正好抵消了光速的差别。
但是爱因斯坦认为根本不需要借助以太也能解释,只需要相信光速不变并且不依赖于介质传播即可。没有以太,相对性原理将继续有效。
之后,爱因斯坦从相对性原理和光速不变两个假设出发,也得到了洛伦兹变换。并且爱因斯坦进一步认为,不只是电磁理论满足洛伦兹变换,一切物理规律都应该满足洛伦兹变换。
于是他把牛顿力学中的伽利略变换升级为了洛伦兹变换,并且正好伽利略变换就是洛伦兹变换在低速情况下的近似。
爱因斯坦从洛伦兹变换出发,得出了一系列令人匪夷所思的新现象,最终得到狭义相对论。
以上,我们从头梳理了狭义相对论提出的逻辑脉络,如果你有一些高等数学的知识并且感兴趣的话,你可以对解狭义相对论有更好的理解。
五、进一步推广
从以上逻辑你可以看出,物理学的发展似乎是一个升级的过程,旧的理论解释力差,或是不精确,或是解释不了所有现象,慢慢就有新的理论被提出。
但是新理论并不是完全推翻旧理论,而是把旧理论囊括进来。
物理学的发展就像大泡泡包裹小泡泡,理论越新,泡泡就越大,它能包裹住里头的旧理论,也就是小泡泡。随着物理学的发展,游离在外头的小泡泡慢慢被更大的泡泡包裹进来。
例如20世纪发展出来的量子力学和狭义相对论就是两个泡泡,结果被一个更大的量子场论的泡泡给包裹了进来。
那么有没有这么一种最大的泡泡,可以包含所有的小泡泡呢?爱因斯坦穷其一生想要寻找的大统一理论就是这个思路。