R语言实战__第9章方差分析

第9章方差分析

名义型或有序因子也可作为预测变量进行建模。当包含的因子是解释变量时，关注的重点通常从预测转向组别差异的分析，这种分析方法称作**方差分析（ANOVA）。

9.1 术语速成

9.2 ANOVA模型拟合

ANOVA也是广义线性模型的特例，可以用lm()函数分析ANOVA模型。不过本章基本使用aov()函数。两者结果等同。

9.2.1 aov( )函数

aov( )函数的语法为`aov(formula, data = dataframe)。

符号及表达式.png

9.2.2 表达式中各项的顺序

因子顺序.png

基础性的效应需要放在表达式前面。首先是协变量，然后是主效应，接着是双因素的交互项，再接着是三因素的交互项，以此类推。

car包中的Anova()函数（不要与标准anova()函数混淆）提供了类型Ⅱ和类型Ⅲ方法的选项，而aov()函数使用的是类型Ⅰ的方法。

9.3 单因素方差分析

单因素方差分析中，比较分类因子定义的两个或多个组别中的因变量均值。

代码清单9-1 单因素方差分析

> library(multcomp)
> attach(cholesterol)
> table(trt)
trt
 1time 2times 4times  drugD  drugE 
    10     10     10     10     10 
> aggregate(response, by=list(trt), FUN=mean)
  Group.1        x
1   1time  5.78197
2  2times  9.22497
3  4times 12.37478
4   drugD 15.36117
5   drugE 20.94752
> aggregate(response, by=list(trt), FUN=sd)
  Group.1        x
1   1time 2.878113
2  2times 3.483054
3  4times 2.923119
4   drugD 3.454636
5   drugE 3.345003
> fit <- aov(response ~ trt)
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
trt          4 1351.4   337.8   32.43 9.82e-13 ***
Residuals   45  468.8    10.4                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> library(gplots)
> plotmeans(response ~ trt, xlab="Treatment", ylab="Response", 
+           main="Mean Plot\nwith 95% CI")
> detach(cholesterol)

ANOVA对治疗方式（ trt）的F检验非常显著（p<0.0001），说明五种疗法的效果不同。

gplots包中的plotmeans()可绘制带有置信区间的组均值图形。

置信区间下组均值图形.png

9.3.1 多重比较

探究各变量之间的不同。TukeyHSD()函数提供了对各组均值差异的成对检验。
代码清单9-2 Tukey HSD的成对组间比较

> TukeyHSD(fit)
  Tukey multiple comparisons of means
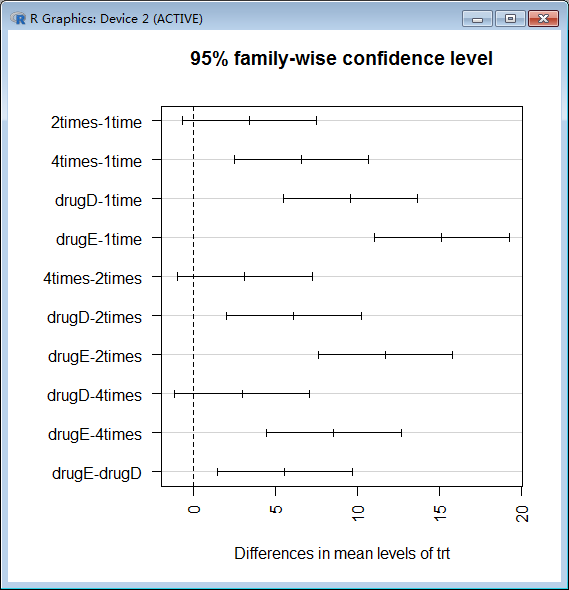
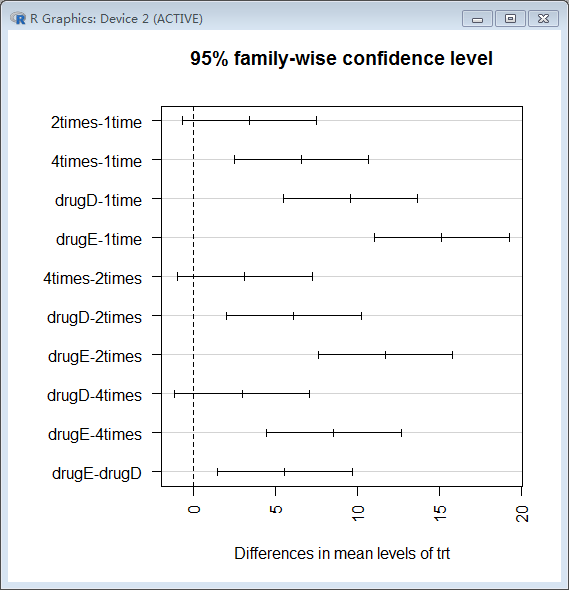
    95% family-wise confidence level

Fit: aov(formula = response ~ trt)

$trt
                  diff        lwr       upr     p adj
2times-1time   3.44300 -0.6582817  7.544282 0.1380949
4times-1time   6.59281  2.4915283 10.694092 0.0003542
drugD-1time    9.57920  5.4779183 13.680482 0.0000003
drugE-1time   15.16555 11.0642683 19.266832 0.0000000
4times-2times  3.14981 -0.9514717  7.251092 0.2050382
drugD-2times   6.13620  2.0349183 10.237482 0.0009611
drugE-2times  11.72255  7.6212683 15.823832 0.0000000
drugD-4times   2.98639 -1.1148917  7.087672 0.2512446
drugE-4times   8.57274  4.4714583 12.674022 0.0000037
drugE-drugD    5.58635  1.4850683  9.687632 0.0030633

> par(las=2) #标签文字方向
> par(mar=c(5, 8, 4, 2)) #图形边距：下、左、上、右
> plot(TukeyHSD(fit))

1time和2times的均值差异不显著（ p=0.138），而1time和4times间的差异非常显著（p<0.001）。

多重比较_置信区间图.png

图中置信区间包含0组别说明差异不显著（p>0.05）。

multcomp包中的glht()函数提供了多重均值比较更为全面的方法，适用于线性模型及广义线性模型。下面的代码重现了Tukey HSD检验，并用不同图形展示结果。

> library(multcomp)
> par(mar=c(5, 4, 6, 2))
> tuk <- glht(fit, linfct=mcp(trt="Tukey"))

multcomp包中glht()函数.png

有相同字母的组说明均值差异不显著。

从结果看，一天四次5mg剂量比一天一次20mg效果更佳。

9.3.2 评估检验的假设条件

单因素方差分析中，假设因变量服从正态分布，各组方差相等。结果的有效性取决于统计检验时数据满足假设条件的程度。

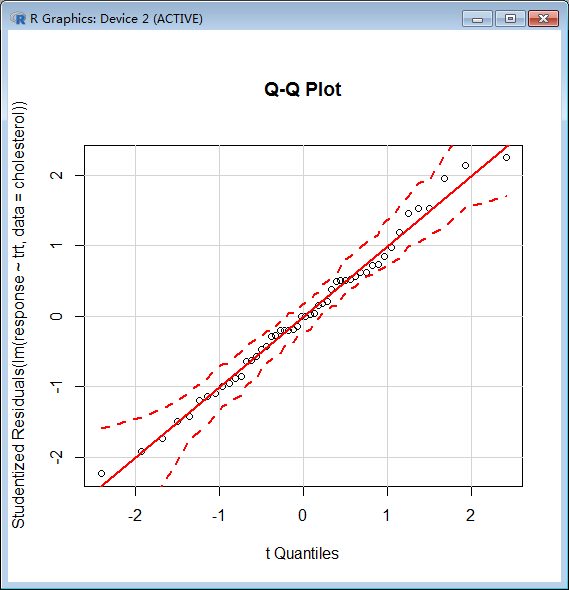
Q-Q图可用来检验正态性假设，若数据落在95%的置信区间内，说明满足正态性假设。

> library(car)
> qqPlot(lm(response ~ trt, data=cholesterol), 
+        simulate=TRUE, main="Q-Q Plot", labels=FALSE)

正态性假设_Q-Q图.png

R提供了一些方差齐性检验的函数。如下代码做Bartlett检验：

> bartlett.test(response ~ trt, data=cholesterol)

        Bartlett test of homogeneity of variances

data:  response by trt
Bartlett's K-squared = 0.57975, df = 4, p-value = 0.9653

p=0.97,五组方差无显著不同。

其他检验如Fligner-Killeen检验（fligner.test()函数）和Brown-Forsythe检验（HH包中的hov()函数）。它们的检验结果与Bartlett检验相同。

方差齐性分析对离群点非常敏感。car包中的outlierTest()函数可检测离群点：

> library(car)
> outlierTest(fit)

No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
   rstudent unadjusted p-value Bonferonni p
19 2.251149           0.029422           NA

当p>1时产生NA，因此说明数据中没有离群点。

综上，根据Q-Q图、Bartlett检验和离群点检验，该数据似乎可以用ANOVA模型很好地拟合。这些方法证明了结果的可靠。

9.4 单因素协方差分析

单因素协方差分析（ANCOVA）扩展了单因素方差分析（ANOVA），包含一个或多个定量的协变量。
代码清单9-3 单因素ANCOVA

> data(litter, package="multcomp")
> table(dose)
dose
  0   5  50 500 
 20  19  18  17 
> aggregate(litter$weight, by=list(litter$dose), FUN=mean) #此处用数据框$变量名
  Group.1        x
1       0 32.30850
2       5 29.30842
3      50 29.86611
4     500 29.64647
> fit <- aov(litter$weight ~ litter$gesttime + dose)
> summary(fit)
                Df Sum Sq Mean Sq F value  Pr(>F)   
litter$gesttime  1  134.3  134.30   8.049 0.00597 **
dose             3  137.1   45.71   2.739 0.04988 * 
Residuals       69 1151.3   16.69                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

利用table()函数可以看到，不同剂量下产仔数不同。
aggregate()函数获得各组均值，未用药幼崽体重均值最高。
ANCOVA的F检验说明：gesttime与weight有关，控制gesstime，dose与weight有关。

由于使用了协变量，可以求去除协变量效应后的组均值。使用effects包中的effects()函数来计算调整的均值：

> library(effects)
> effect("litter$dose", fit)
Error in model.frame.default(litter$weight ~ litter$gesttime + litter$dose +  : 
  参数'litter'的种类(list)不对

本例中，调整的均值与aggregate()函数得出的未调整的均值类似。

F检验表明了不同处理方式造成体重均值不同，但无法表明哪种处理方式与其他方式不同。使用multcomp包对所有均值进行比较。multcomp包还可以检验用户自定义的均值假设。
代码清单9-4 对用户定义的对照的多重比较

> library(multcomp)
> contrast <- rbind("no drug vs. drug" = c(3, -1, -1, -1))
> summary(glht(fit, linfct=mcp(dose=contrast)))
Error in mcp2matrix(model, linfct = linfct) : 
  Variable(s) ‘dose’ have been specified in ‘linfct’ but cannot be found in ‘model’! 
> #遇错未实现

9.4.1 评估检验的假设条件

ANCOVA与ANOVA相同，都需要正态性和同方差性假设，9.3.2中方法可以检验这些假设条件。

另外ANCOVA还假订回归斜率相同。模型包含交互项时，可对回归斜率的同质性进行检验。

代码清单9-5 检验回归斜率的同质性

> library(multcomp)
> fit2 <- aov(weight ~ gesttime*dose, data=litter)
> summary(fit2)
              Df Sum Sq Mean Sq F value  Pr(>.4.2 koF)   
gesttime       1  134.3  134.30   8.289 0.00537 **
dose           3  137.1   45.71   2.821 0.04556 * 
gesttime:dose  3   81.9   27.29   1.684 0.17889   
Residuals     66 1069.4   16.20                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

交互效应不显著，支持了斜率相等的假设。

若假设不成立，可尝试变换协变量或因变量，或使用能对每个斜率独立解释的模型，或使用不需假设回归斜率同质性的非参数ANCOVA方法。sm包中的sm.ancova()函数为后者提供了一个例子。

9.4.2 结果可视化

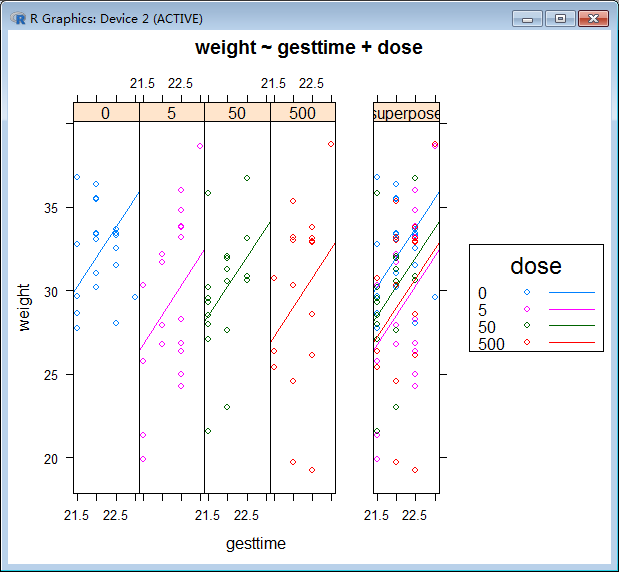
HH包中的ancova()函数可以绘制因变量、协变量和因子之间的关系图。例如代码：

> library(HH)
> ancova(weight ~ gesttime + dose, data=litter)
Analysis of Variance Table

Response: weight
          Df  Sum Sq Mean Sq F value   Pr(>F)   
gesttime   1  134.30 134.304  8.0493 0.005971 **
dose       3  137.12  45.708  2.7394 0.049883 * 
Residuals 69 1151.27  16.685                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

ancova()函数可视化.png

9.5 双因素方差分析

在双因素方差分析中，受试者被分配到两因子的交叉类别组中。

> attach(ToothGrowth)
> table(supp, dose)
    dose
supp 0.5  1  2
  OJ  10 10 10
  VC  10 10 10
> aggregate(len, by=list(supp, dose), FUN=mean)
  Group.1 Group.2     x
1      OJ     0.5 13.23
2      VC     0.5  7.98
3      OJ     1.0 22.70
4      VC     1.0 16.77
5      OJ     2.0 26.06
6      VC     2.0 26.14
> aggregate(len, by=list(supp, dose), FUN=sd)
  Group.1 Group.2        x
1      OJ     0.5 4.459709
2      VC     0.5 2.746634
3      OJ     1.0 3.910953
4      VC     1.0 2.515309
5      OJ     2.0 2.655058
6      VC     2.0 4.797731
> fit <- aov(len ~ supp*dose)
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4  12.317 0.000894 ***
dose         1 2224.3  2224.3 133.415  < 2e-16 ***
supp:dose    1   88.9    88.9   5.333 0.024631 *  
Residuals   56  933.6    16.7                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

table语句表明该设计为均衡设计（各设计单元中样本大小相同），aggregate获得各单元均值和标准差。summary()函数得到方差分析表，可以看到主效应（supp和dose）和交互效应都非常显著。

有多种结果可视化处理，

interaction.plot()函数

> interaction.plot(dose, supp, len, type="b", col=c("red", "blue"), pch=c(16, 18), main="Interaction between Dose and Supplement Type")

interaction.plot().png

gplots包中plotmeans()函数

> library(gplots)
> plotmeans(len ~ interaction(supp, dose, sep=" "),
+           connect=list(c(1, 3, 5),c(2, 4, 6)),  #1，3，5为一组连线
+           col=c("red","darkgreen"),
+           main = "Interaction Plot with 95% CIs", 
+           xlab="Treatment and Dose Combination")

plotmeans().png

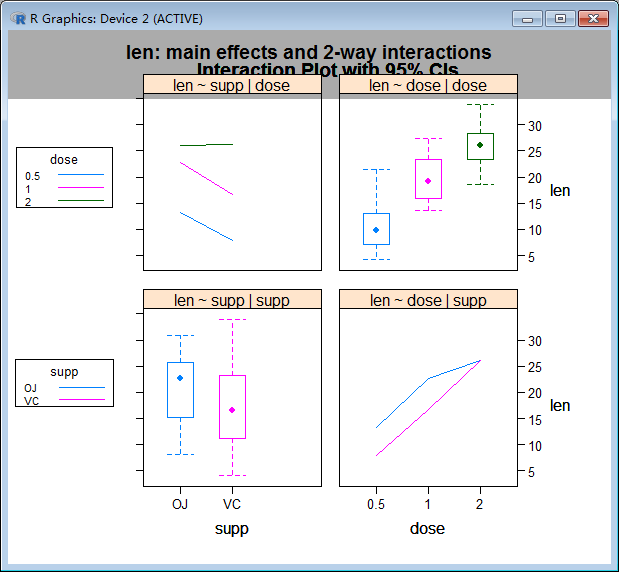
最后，还可用HH包中的interaction2wt()函数可视化结果：

> library(HH)
> interaction2wt(len~supp*dose)

interaction2wt.png

9.6 重复测量方差分析

所谓重复测量方差分析，即受试者被测量不止一次。本节重点关注含一个组内和一个组间因子的重复测量方差分析。

代码清单9-7 含一个组内因子和一个组间因子的重复测量方差分析

> CO2$conc <- factor(CO2$conc)
> wlbl <- subset(CO2, Treatment='chilled')
> fit <- aov(uptake ~ (conc*Type) + Error(Plant/(conc)), wlbl)
> summary(fit)

Error: Plant
          Df Sum Sq Mean Sq F value  Pr(>F)    
Type       1   3366    3366   22.49 0.00079 ***
Residuals 10   1497     150                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Error: Plant:conc
          Df Sum Sq Mean Sq F value   Pr(>F)    
conc       6   4069   678.1 101.322  < 2e-16 ***
conc:Type  6    374    62.4   9.324 3.23e-07 ***
Residuals 60    402     6.7                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
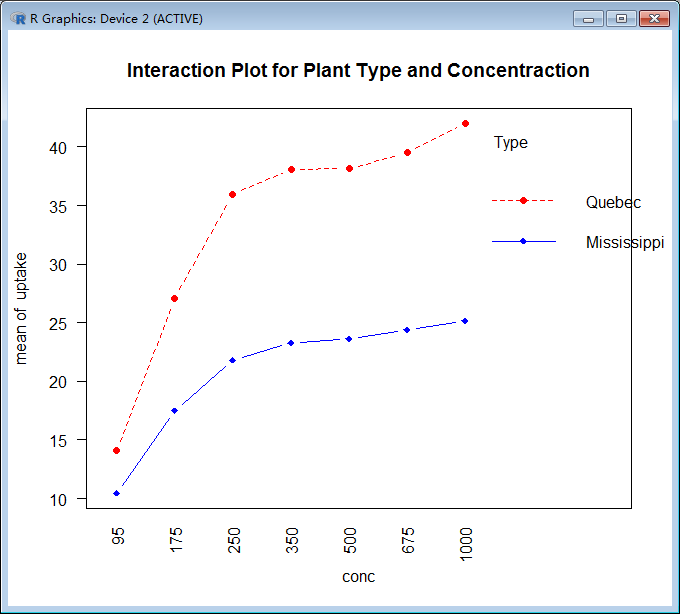
> par(las=2)
> par=(mar=c(10, 4, 4, 2))
> with(wlbl, interaction.plot(conc, Type, uptake, type="b", col=c("red", "blue"), pch=c(16, 18), main="Interaction Plot for Plant Type and Concentraction"))
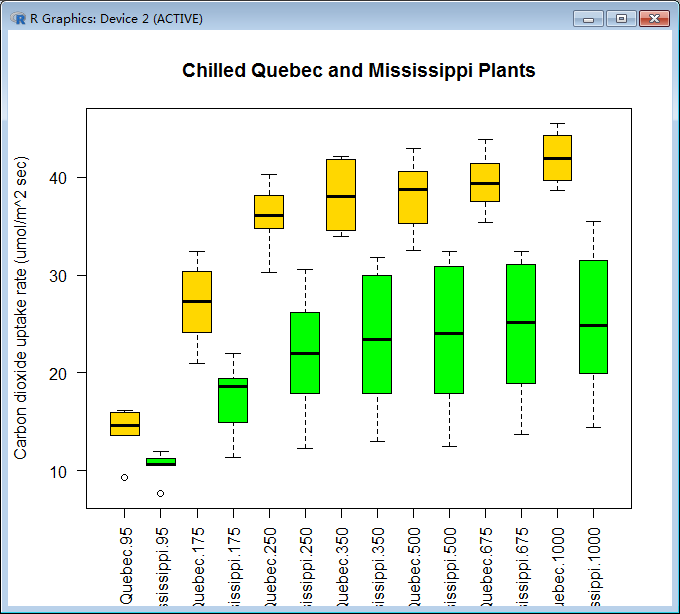
> boxplot(uptake ~ Type*conc, data=wlbl, col=(c("gold", "green")), 
+         main = "Chilled Quebec and Mississippi Plants", 
+         ylab = "Carbon dioxide uptake rate (umol/m^2 sec)")

方差分析表明在0.01水平下，主效应类型和浓度以及交叉效应类型x浓度都非常显著。

interaction.plot函数绘图.png

boxplot函数绘图.png

通常处理的数据集是宽格式（wide format），即列是变量，行是观测值，而且一行一个受试对象。9.4节中litter数据库即为此类。
不过在处理重复测量设计时，需要有长格式（long format）数据才能拟合模型。长格式中，因变量的每次测量都要放到它独有的行中，CO2数据集即是该种形式。5.6.3节中的reshape包可方便地将数据转换为相应的格式。

以上分析均针对单个因变量的情况。

9.7 多元方差分析

当因变量（结果变量）不止一个时，可用多元方差分析（MANOVA）对它们同时进行分析。

代码清单9-8 单因素多元方差分析

> library(MASS)
> attach(UScereal)
> y <- cbind(calories, fat, sugars)
> aggregate(y, by=list(shelf), FUN=mean)
  Group.1 calories       fat    sugars
1       1 119.4774 0.6621338  6.295493
2       2 129.8162 1.3413488 12.507670
3       3 180.1466 1.9449071 10.856821
> cov(y)
           calories       fat     sugars
calories 3895.24210 60.674383 180.380317
fat        60.67438  2.713399   3.995474
sugars    180.38032  3.995474  34.050018
> fit <- manova(y ~ shelf)
> summary(fit)
          Df  Pillai approx F num Df den Df  Pr(>F)   
shelf      1 0.19594    4.955      3     61 0.00383 **
Residuals 63                                          
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> summary.aov(fit)
 Response calories :
            Df Sum Sq Mean Sq F value    Pr(>F)    
shelf        1  45313   45313  13.995 0.0003983 ***
Residuals   63 203982    3238                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 Response fat :
            Df  Sum Sq Mean Sq F value   Pr(>F)   
shelf        1  18.421 18.4214   7.476 0.008108 **
Residuals   63 155.236  2.4641                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 Response sugars :
            Df  Sum Sq Mean Sq F value  Pr(>F)  
shelf        1  183.34  183.34   5.787 0.01909 *
Residuals   63 1995.87   31.68                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

manova()函数能对组间差异进行多元检验。
summary.aov()函数对每一个变量做单因素方差分析。

9.7.1 评估假设检验

单因素多元方差分析有两个前提假设：

多元正态性（因变量组成的向量服从多元正态分布），可用Q-Q图检验。
方差-协方差矩阵同质性（各组的协方差矩阵相同），通常用Box's M检验，该函数自寻。

代码清单9-9 检验多元正态性

> center <- colMeans(y)
> n <- nrow(y)
> p <- ncol(y)
> cov <- cov(y)
> d <- mahalanobis(y, center, cov)
> coord <- qqplot(qchisq(ppoints(n), df=p),
+                 d, main="Q-Q Plot Assessing Multivariate Normality",
+                 ylab="Mahalanobis D2")
> abline(a=0, b=1)
> identify(coord$x, coord$y, labels=row.names(UScereal))

检验多元正态性Q-Q图.png

若数据服从多元正态分布，那么点将落在斜率为1、截距项为0的直线上。

9.7.2 稳健多元方差分析

如果多元正态性或者方差-协方差均值假设都不满足，或担心多元离群点。可以考虑用稳健或非参数版本的MANOVA检验。稳健单因素MANOVA可通过rrcov包中的Wilks.test()函数实现。vegan包中的adonis()函数提供了非参数的MANOVA的等同形式。下面是Wilks.test()的应用。
代码清单9-10 稳健单因素MANOVA

fit.lm <- lm(response ~ trt, data=cholesterol)
summary(fit.lm)
contrasts(cholesterol$trt)
#系统bug无数据

9.8 用回归来做ANOVA

9.2节提到ANOVA和回归都是广义线性模型的特例。因此本章所有的设计都可用lm()函数来分析。但是，为更好理解结果，需明白在拟合模型是，R是如何理解类别型变量的。

> #aov()函数拟合模型
> fit.aov <- aov(response ~ trt, data=cholesterol)
> summary(fit)
          Df Pillai approx F num Df den Df    Pr(>F)    
shelf      2 0.4021   5.1167      6    122 0.0001015 ***
Residuals 62                                            
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

> #lm()函数拟合模型
> fit.lm <- lm(response ~ trt, data=cholesterol)
> summary(fit.lm)

Call:
lm(formula = response ~ trt, data = cholesterol)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.5418 -1.9672 -0.0016  1.8901  6.6008 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.782      1.021   5.665 9.78e-07 ***
trt2times      3.443      1.443   2.385   0.0213 *  
trt4times      6.593      1.443   4.568 3.82e-05 ***
trtdrugD       9.579      1.443   6.637 3.53e-08 ***
trtdrugE      15.166      1.443  10.507 1.08e-13 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.227 on 45 degrees of freedom
Multiple R-squared:  0.7425,    Adjusted R-squared:  0.7196 
F-statistic: 32.43 on 4 and 45 DF,  p-value: 9.819e-13

因为线性模型要求预测变量是数值型，当lm()函数遇到因子时，会用一系列与因子水平对应的数值对照变量来代替因子。如果因子有k个水平，将会创建k-1个对照变量。R提供了五种创建对照变量的内置方法。默认情况下，对照处理用于无序因子，正交多项式用于有序因子。

内置对照.png

contrasts()函数查看编码过程：

> contrasts(cholesterol$trt)
       2times 4times drugD drugE
1time       0      0     0     0
2times      1      0     0     0
4times      0      1     0     0
drugD       0      0     1     0
drugE       0      0     0     1

修改lm()中默认的对照方法。例如使用Helmert对照：

> fit.lm <- lm(response ~ trt, data=cholesterol, contrasts="contr.helmert")
> #修改
> options(contrasts = c("contr.SAS", "contr.helmert"))

9.9 小结

基本实验和准实验设计的分析方法：ANOVA/ANCOVA/MANOVA。组内和组间设计，单因素ANOVA、单因素ANCOVA、双因素ANOVA、重复测量ANOVA和单因素MANOVA。

下章介绍功效分析，功效分析可以帮助我们在给定置信度的情况下，判断达到要求效果所需样本大小。

——2017.3.7
——于510

R语言实战__第9章 方差分析

第9章 方差分析