一.两个有序数组的排顺
如果有两个有序的数组合并为一个有序数组,我们可以用下面的代码实现:
public void merge(int[] a, int[] b, int[] c){
int i=0,j=0,k=0;
while (i其中数组a,b为我们已经排好序的两个升序数组,c为我们新建的一个长度为a,b两数组相加的一个空数组。
我们用一组测试用例来测试上述算法,并加上log使之更加清晰:
public class TwoListSort {
public static void main(String args[]){
int[] a = {2,6,11 }; //声明数组
int[] b = {8,9,9,15};
int[] c = new int[7];
merge(a,b,c);
}
public static void merge(int[] a, int[] b, int[] c){
int i=0,j=0,k=0;
while (ilog输出为:
2,0,0,0,0,0,0, i = 1, j = 0, k = 1
2,6,0,0,0,0,0, i = 2, j = 0, k = 2
2,6,8,0,0,0,0, i = 2, j = 1, k = 3
2,6,8,9,0,0,0, i = 2, j = 2, k = 4
2,6,8,9,9,0,0, i = 2, j = 3, k = 5
2,6,8,9,9,11,0, i = 3, j = 3, k = 6
2,6,8,9,9,11,15, i = 3, j = 4, k = 7
我们对照log来分析一下上述过程:
初始:i=0,j=0,k=0;
a[0]b[0]
c[2] = b[0] = 8;
c = 2,6,8,0,0,0,0, i = 2, j = 1, k = 3
a[2]>b[1]
c[3] = b[1] = 9;
c = 2,6,8,9,0,0,0, i = 2, j = 2, k = 4
a[2]>b[2]
c[4] = b[2] = 9;
c = 2,6,8,9,9,0,0, i = 2, j = 3, k = 5
a[2] 上面算法设置的非常巧妙,大家可以多测试几组用例,针对不同情况做出分析。
二.无序数组的排序
现在假设有一个无序数组需要排序,但是可以人为的通过一定操作划分为两个有序的数组A和B,那么我们借助上述算法可以很快的将A和B两个有序的子数组进行归并排序。
现在有一个无序数组需要排序,并且他是完全无序的,不能划分为任何有序数组,这个时候需要怎么排序呢?这个问题可以转换为,上一种情况中,A和B两个子数组也是无序的,那么我们可以继续将A和B两个数组拆分下去,拆成更小的子数组:a1,a2和b1,b2...如此下去,我们一直将子数组拆分到最小元素,即一个子数组只有一个元素(也就是拆分成一个个元素,每个元素视为长度为1的数组),那么这一个个长度为1的数组,就可以视为有序数组了(毕竟他只有一个元素)。
那么此时我们可以两个元素,视为“一.两个有序数组的排顺”情况中的A.B两个数组,然后两两合并,知道合并为最初长度的数组,可以看到,这实际上是一个递归的过程。
看到这里不理解的话没关系,我们会在代码中带大家一步步分析:
public class MergeSort {
public static void main(String args[]){
int[] nums = {27, 8, 57, 9, 23, 41, 65, 19, 0, 1, 2 }; //声明数组
mergeSort(nums);
}
//归并排序
public static void mergeSort(int[] arr){
int[] temp =new int[arr.length] ;
internalMergeSort(arr, temp, 0, arr.length-1);
}
private static void internalMergeSort(int[] a, int[] b, int left, int right){
if (left上面展示的就是一个归并排序的过程,internalMergeSort(int[] a, int[] b, int left, int right)该方法就是拆分数组为一个个最小子元素的方法,可以看到该方法中动用了递归调用;mergeSortedArray(int arr[], int temp[], int left, int middle, int right)则是“一.两个有序数组的排顺”情况中将两个有序数组排序的算法,也就是归并方法:
我们给上述两个方法加上必要的log:
private static void internalMergeSort(int[] a, int[] b, int left, int right){
//当left==right的时,已经不需要再划分了
if (left private static void mergeSortedArray(int arr[], int temp[], int left, int middle, int right){
System.out.println("");
System.out.println( "(left合并 , middle合并,right合并) = " + " (" + left + "," + middle + "," + right + ") " );
System.out.print("排序前:");
for(int h = left; h < right +1; h++) {
System.out.print( arr[h] + ",");
}
int i=left;
int j=middle+1;
int k=0;
while ( i<=middle && j<=right){ // 逐个归并
if (arr[i] <=arr[j]){
temp[k++] = arr[i++];
} else{
temp[k++] = arr[j++];
}
}
while (i <=middle){ // 将左边剩余的归并
temp[k++] = arr[i++];
}
while ( j<=right){ // 将右边剩余的归并
temp[k++] = arr[j++];
}
for (i=0; i由于运行的结果比较长,我们将在下面的分析中逐步分开讲解:
下面我们来分析一遍上面的结果——首先是第一部分:
(left左 , middle左,right左) = (0,5,10)
27,8,57,9,23,41,65,19,0,1,2,
(left左 , middle左,right左) = (0,2,5)
27,8,57,9,23,41,
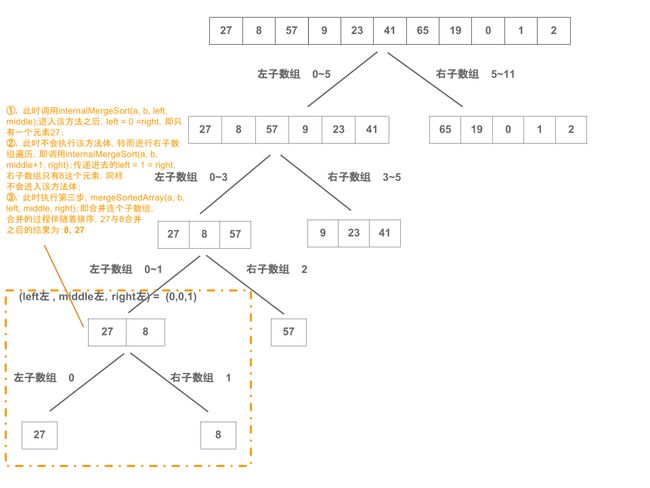
(left左 , middle左,right左) = (0,1,2)
27,8,57,
(left左 , middle左,right左) = (0,0,1)
27,8,
(left右 , middle右,right右) = (0,1,1)
8,
(left合并 , middle合并,right合并) = (0,0,1)
排序前:27,8,
排序后:8,27,
这个部分的log代表的过程图示如下,即第一次循环遍历到左子树的最底层,开始向上归并一层,归并的过程伴随着排序:
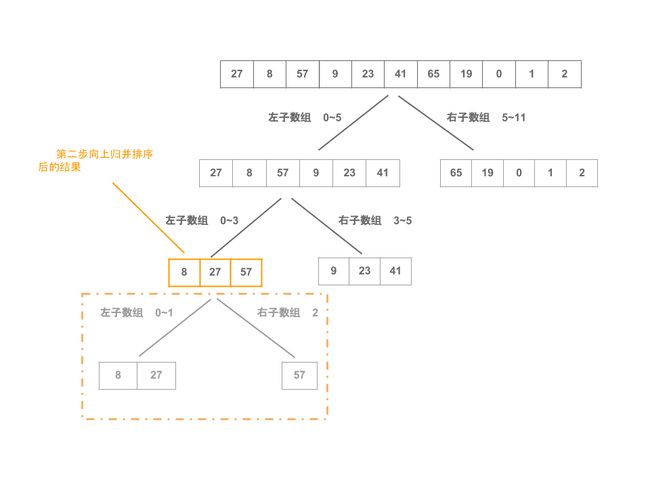
归并后的结果为8,27,然后向上递归调用,再归并一层:
(left右 , middle右,right右) = (0,2,2)
57,
(left合并 , middle合并,right合并) = (0,1,2)
排序前:8,27,57,
排序后:8,27,57,
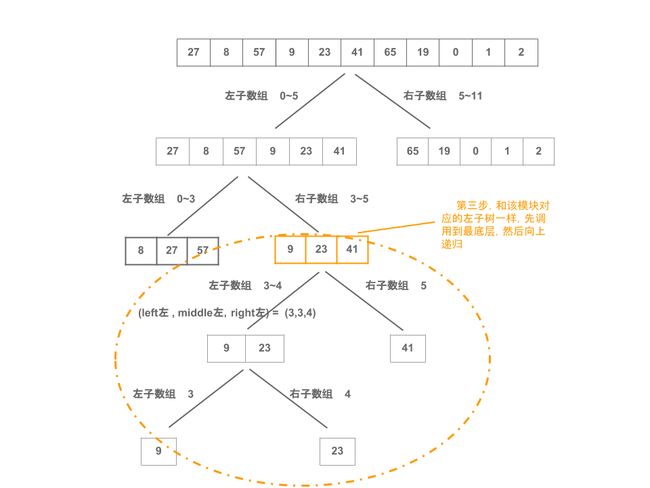
接着归并第三层:
(left右 , middle右,right右) = (0,3,5)
9,23,41,
(left左 , middle左,right左) = (3,4,5)
9,23,41,
(left左 , middle左,right左) = (3,3,4)
9,23,
(left右 , middle右,right右) = (3,4,4)
23,
(left合并 , middle合并,right合并) = (3,3,4)
排序前:9,23,
排序后:9,23,
(left右 , middle右,right右) = (3,5,5)
41,
(left合并 , middle合并,right合并) = (3,4,5)
排序前:9,23,41,
排序后:9,23,41,
(left合并 , middle合并,right合并) = (0,2,5)
排序前:8,27,57,9,23,41,
排序后:8,9,23,27,41,57,
这一步就是合并8,27,57和9,23,41这两个有序子数组,毕竟这两个子数组的底层已经递归调用完了,然后合并的过程中伴随着排序,最终得到第二层有序的左子数组:8,9,23,27,41,57,
接着是同样的递归合并第二层右子数组:
(left右 , middle右,right右) = (0,6,10)
65,19,0,1,2,
(left左 , middle左,right左) = (6,8,10)
65,19,0,1,2,
(left左 , middle左,right左) = (6,7,8)
65,19,0,
(left左 , middle左,right左) = (6,6,7)
65,19,
(left右 , middle右,right右) = (6,7,7)
19,
(left合并 , middle合并,right合并) = (6,6,7)
排序前:65,19,
排序后:19,65,
(left右 , middle右,right右) = (6,8,8)
0,
(left合并 , middle合并,right合并) = (6,7,8)
排序前:19,65,0,
排序后:0,19,65,
(left右 , middle右,right右) = (6,9,10)
1,2,
(left左 , middle左,right左) = (9,9,10)
1,2,
(left右 , middle右,right右) = (9,10,10)
2,
(left合并 , middle合并,right合并) = (9,9,10)
排序前:1,2,
排序后:1,2,
(left合并 , middle合并,right合并) = (6,8,10)
排序前:0,19,65,1,2,
排序后:0,1,2,19,65,
最后是归并第二层已经拍好队的两个有序子数组:8,9,23,27,41,57,和0,1,2,19,65,,最终得到有序的原数组:
(left合并 , middle合并,right合并) = (0,5,10)
排序前:8,9,23,27,41,57,0,1,2,19,65,
排序后:0,1,2,8,9,19,23,27,41,57,65,