-
- Validate Binary Search Tree
-
- Same Tree (基础)
- 101.symmetric tree (基础)
-
- Maximum Depth of Binary Tree
-
- Construct Binary Tree from Preorder and Inorder Traversal
- 106、 中序后序构建二叉树
-
- Convert Sorted Array to Binary Search Tree
-
- Convert Sorted List to Binary Search Tree
-
- Balanced Binary Tree
-
- Minimum Depth of Binary Tree
-
- Path Sum (重要)
- 113.path sum II (重要)
-
- Flatten Binary Tree to Linked List (理解)
-
- Populating Next Right Pointers in Each Node
-
- Populating Next Right Pointers in Each Node II
-
- Sum Root to Leaf Numbers
- 130 . Surrounded Regions
-
- Clone Graph
-
- Binary Tree Right Side View
-
- Number of Islands
-
- Course Schedule (重要)
-
- Binary Tree Paths
-
- Reconstruct Itinerary
-
- House Robber III (重要)
98. Validate Binary Search Tree
验证是否是二叉搜索树。采用DFS思想。
class Solution(object):
def isValidBST(self, root):
return self.isValidBSTRecu(root, float("-inf"), float("inf"))
def isValidBSTRecu(self, root, low, high):
if root is None:
return True
return low < root.val and root.val < high \
and self.isValidBSTRecu(root.left, low, root.val) \
and self.isValidBSTRecu(root.right, root.val, high)
100. Same Tree
Given two binary trees, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical and the nodes have the same value.
最暴力直接的方法:
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def isSameTree(self, p, q):
"""
:type p: TreeNode
:type q: TreeNode
:rtype: bool
"""
res1, res2 = [], []
self.preOrdersort(p, res1)
self.preOrdersort(q, res2)
if len(res1) != len(res2):
return False
for i in xrange(0, len(res1)):
if res1[i] != res2[i]:
return False
return True
def preOrdersort(self, node, res):
if node == None:
res.append(None)
else:
res.append(node.val)
self.preOrdersort(node.left, res)
self.preOrdersort(node.right,res)
但比较简单的方法如下:
class Solution2:
# @param p, a tree node
# @param q, a tree node
# @return a boolean
def isSameTree(self, p, q):
if p is None and q is None:
return True
if p is not None and q is not None:
return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
return False
101.symmetric tree
判断树是否是对称树
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3
But the following [1,2,2,null,3,null,3] is not:
1
/ \
2 2
\ \
3 3
肯定是使用递归求解,从左右两个支树出发
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if root is None:
return True
return self.symmetric(root.right,root.left)
def symmetric(self, p, q):
if p is None and q is None:
return True
if p is None or q is None or p.val != q.val:
return False
return self.symmetric(p.left, q.right) and self.symmetric(p.right, q.left)
另一种思路:
class Solution:
# @param root, a tree node
# @return a boolean
def isSymmetric(self, root):
if root is None:
return True
stack = []
stack.append(root.left)
stack.append(root.right)
while stack:
p, q = stack.pop(), stack.pop()
if p is None and q is None:
continue
if p is None or q is None or p.val != q.val:
return False
stack.append(p.left)
stack.append(q.right)
stack.append(p.right)
stack.append(q.left)
return True
104. Maximum Depth of Binary Tree
求一个二叉树的最大深度。属于常规的递归求解问题。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
105. Construct Binary Tree from Preorder and Inorder Traversal
Given preorder and inorder traversal of a tree, construct the binary tree.
给定一个树的前序和中序遍历,构建这个树。
思路如下:
先序遍历的第一个数一定是根节点,而中序遍历中根据根节点可以将树分为左右两个子树,依次递归既可以得到这个完整的树。
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
lookup = {}
for i, item in enumerate(inorder):
lookup[item] = i
return self.constrctTree(lookup, preorder, inorder, 0, 0, len(inorder))
def constrctTree(self, lookup, preorder, inorder,pre_start,in_start,in_end):
if in_start == in_end:
return None
node = TreeNode(preorder[pre_start]) # root node
i = lookup[preorder[pre_start]]
node.left = self.constrctTree(lookup, preorder, inorder, pre_start+1, in_start, i)
node.right = self.constrctTree(lookup, preorder, inorder, pre_start + 1 + i - in_start, i+1, in_end)
return node
还是有很多疑问,constrctTree(self, lookup, preorder, inorder,pre_start,in_start,in_end)中每个参数代表的含义是什么。
更符合常规理解的解法为:
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
if inorder:
index = inorder.index(preorder[0])
del preorder[0]
root = TreeNode(inorder[index])
root.left = self.buildTree(preorder, inorder[:index])
root.right = self.buildTree(preorder, inorder[index + 1:])
return root
106、 中序后序构建二叉树
class Solution(object):
def buildTree(self, inorder, postorder):
"""
:type inorder: List[int]
:type postorder: List[int]
:rtype: TreeNode
"""
if inorder:
index = inorder.index(postorder.pop())
root = TreeNode(inorder[index])
# 下面两行调换位置就不可以,为什么
root.right = self.buildTree(inorder[index+1:], postorder)
root.left = self.buildTree(inorder[:index], postorder)
return root
class Solution:
# @param inorder, a list of integers
# @param postorder, a list of integers
# @return a tree node
def buildTree(self, inorder, postorder):
lookup = {}
for i, num in enumerate(inorder):
lookup[num] = i
return self.buildTreeRecu(lookup, postorder, inorder, len(postorder), 0, len(inorder))
def buildTreeRecu(self, lookup, postorder, inorder, post_end, in_start, in_end):
if in_start == in_end:
return None
node = TreeNode(postorder[post_end - 1])
i = lookup[postorder[post_end - 1]]
node.left = self.buildTreeRecu(lookup, postorder, inorder, post_end - 1 - (in_end - i - 1), in_start, i)
node.right = self.buildTreeRecu(lookup, postorder, inorder, post_end - 1, i + 1, in_end)
return node
总结105和106两个题,有两种思路,但主思想都是根据先序或后序遍历找到根节点,在由根节点找到中序遍历中序号,由序号确定左右子树,重复这个过程,直到二叉树构建完毕。
对第一种,思路比较简单,找到序号后,重复这个过程,但是要注意对preorder的处理。对先序遍历[1,2,4,5,3,6,7]来说,1是整个树的根节点,2是左子树的根节点,但如何确定右子树呢,采用动态弹出方式,因为构建左子树时先序中确定的是[4,2,5],因此,构建完左子树后先序遍历变为[3,6,7],再执行构建右子树。需要明确的有:
1、由于对先序列表执行删除操作,左右子树先后顺序十分重要,需要明确105和106的区别
2、在python中传递的是变量的引用。
第二种方法整体流程没有大问题,通过使用字典提高查找速度,由于对列表不删除,因此对根节点的定位比较关键。对左子树来说根节点位置是pre_start+1没问题,但是右子树中为什是是pre_start + 1 + i - in_start,这个表达式分为2个部分,第一个是pre_start+1,第二是i-in_start
留作进一步理解。
108. Convert Sorted Array to Binary Search Tree
Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
给定一个升序列表,转换为一个平衡二叉树。
初步想法分为两个步骤,一是找到中间节点作为根节点,然后递归
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if nums:
mid = len(nums) / 2
node = TreeNode(nums[mid])
node.left = self.sortedArrayToBST(nums[:mid])
node.right = self.sortedArrayToBST(nums[mid+1:])
return node
109. Convert Sorted List to Binary Search Tree
这道题和108的最大区别在于108的升序列表这里采用链表表示。
class ListNode(object):
def __init__(self, x):
self.val = x
self.next = None
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def sortedListToBST(self, head):
"""
:type head: ListNode
:rtype: TreeNode
"""
p_current = head
val_lsit = []
while p_current:
val_lsit.append(p_current.val)
p_current = p_current.next
return self.sortedArrayToBST(val_lsit)
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if nums:
mid = len(nums) / 2
node = TreeNode(nums[mid])
node.left = self.sortedArrayToBST(nums[:mid])
node.right = self.sortedArrayToBST(nums[mid+1:])
return node
整体思路还是没有变。
110. Balanced Binary Tree
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
这道题还是有点难度。
class Solution(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if root is None:
return True
left = self.getDepth(root.left)
right = self.getDepth(root.right)
if abs(left-right) > 1:
return False
else:
return self.isBalanced(root.left) and self.isBalanced(root.right)
def getDepth(self,root):
if root is None:
return 0
return 1 + max(self.getDepth(root.left), self.getDepth(root.right))
上面这种解法效率在24%,主要思路是从根节点开始,依次计算左右两边子树的最大深度,如果根节点平衡,在递归判断下面节点是否平衡。这样从上往下带来的最大问题就是造成大部分计算的重复。
如何进一步提升效率?
看看discuss 里最受欢迎的那个,我靠,不是和我一样嘛
public class Solution {
public boolean isBalanced(TreeNode root) {
if(null == root) {
return true;
}
return Math.abs(height(root.left) - height(root.right)) < 2 && isBalanced(root.left) && isBalanced(root.right);
}
public int height(TreeNode root) {
if(null == root) {
return 0;
}
return 1 + Math.max(height(root.left), height(root.right));
}
}
111. Minimum Depth of Binary Tree
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
以下理解出现偏差,最短距离指的是从根节点到叶子节点的最短距离。
所以要先判断一个节点是不是叶节点,如果左右子树都为None,就是叶节点。
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
if root.right is None and root.left is None:
return 1
if root.right and root.left:
return min(self.minDepth(root.left), self.minDepth(root.right)) + 1
if root.left:
return self.minDepth(root.left) + 1
if root.right:
return self.minDepth(root.right) + 1
这写的还是随意了点,效率也比较低。但主要考虑的细节有:如果左右支树都有元素,则要取最小。如果只有某一子树有元素,则说明不是叶子节点,还需要继续寻找。
class Solution:
# @param root, a tree node
# @return an integer
def minDepth(self, root):
if root is None:
return 0
if root.left and root.right:
return min(self.minDepth(root.left), self.minDepth(root.right)) + 1
else:
return max(self.minDepth(root.left), self.minDepth(root.right)) + 1
参考:
public class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
return getMin(root);
}
public int getMin(TreeNode root){
if (root == null) {
return Integer.MAX_VALUE;
}
if (root.left == null && root.right == null) {
return 1;
}
return Math.min(getMin(root.left), getMin(root.right)) + 1;
}
}
112. Path Sum
Given a binary tree and a sum, determine if the tree has a root-to-leaf path
such that adding up all the values along the path equals the given sum.
For example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
给定一个数和一个值,确定是否存在一条路径使value之和等于该值。
最直观的做法就是将所有根节点到叶节点的路径计算一遍,再判断。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
# @param root, a tree node
# @param sum, an integer
# @return a boolean
def hasPathSum(self, root, sum):
if root is None:
return False
if root.left is None and root.right is None and root.val == sum:
return True
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
113. Path Sum II
Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
For example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
return
[
[5,4,11,2],
[5,8,4,5]
]
class Solution(object):
def pathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: List[List[int]]
"""
if not root: return []
if root.left is None and root.right is None:
if sum == root.val:
return [[root.val]]
else:
return []
a = self.pathSum(root.left, sum - root.val) + \
self.pathSum(root.right, sum - root.val)
return [[root.val] + i for i in a]
def pathSum(self, root, sum):
if not root:
return []
if not root.left and not root.right and sum == root.val:
return [[root.val]]
tmp = self.pathSum(root.left, sum-root.val) + self.pathSum(root.right, sum-root.val)
return [[root.val]+i for i in tmp]
class Solution:
def pathSum(self, root, sum):
if not root:
return []
val, kids = root.val, (root.left, root.right)
if any(kids):
return [[val] + path
for kid in kids
for path in self.pathSum(kid, sum - val)]
return [[val]] if val == sum else []
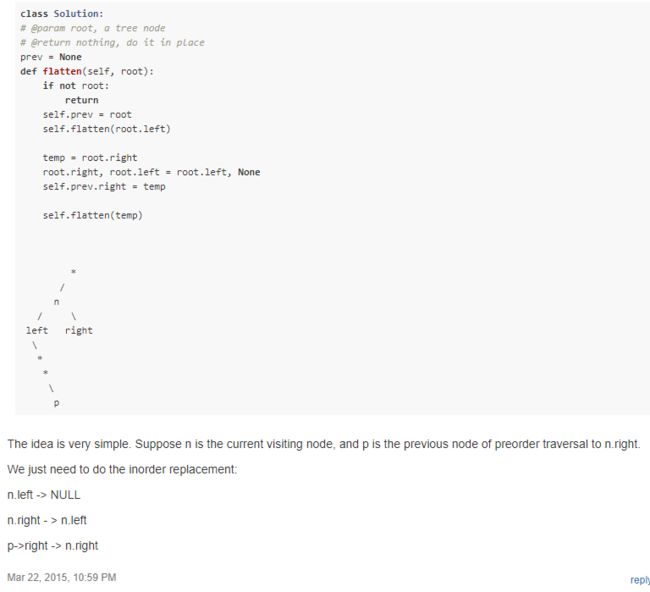
114. Flatten Binary Tree to Linked List
Given a binary tree, flatten it to a linked list in-place.
For example,
Given
1
/ \
2 5
/ \ \
3 4 6
The flattened tree should look like:
1
\
2
\
3
\
4
\
5
\
6
If you notice carefully in the flattened tree, each node's right child points to the next node of a pre-order traversal.
主要思路是先用先序遍历整个树,然后依次重构成链状。
class Solution(object):
def flatten(self, root):
"""
:type root: TreeNode
:rtype: void Do not return anything, modify root in-place instead.
"""
res = []
self.preorderSort(root,res)
for i in xrange(1,len(res)):
res[i-1].left = None
res[i-1].right = res[i]
def preorderSort(self,root,res):
if root:
res.append(root)
self.inorderSort(root.left,res)
self.inorderSort(root.right,res)
树的遍历比较基础,但值得注意的是还有用栈的方式,不用递归,如下:
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
if root == None:return []
stack = [root]
result = []
while len(stack) != 0:
tmp_root = stack.pop()
if tmp_root == None:continue
result.append(tmp_root)
stack.append(tmp_root.right)
stack.append(tmp_root.left)
return result
上面这种方法效率还不是很高。
上面思路还是有点没有理解。
class Solution1:
# @param root, a tree node
# @return nothing, do it in place
def flatten(self, root):
return self.flattenRecu(root, None)
def flattenRecu(self, root, list_head):
if root != None:
list_head = self.flattenRecu(root.right, list_head)
list_head = self.flattenRecu(root.left, list_head)
root.right = list_head
root.left = None
return root
else:
return list_head
class Solution2:
list_head = None
# @param root, a tree node
# @return nothing, do it in place
def flatten(self, root):
if root != None:
self.flatten(root.right)
self.flatten(root.left)
root.right = self.list_head
root.left = None
self.list_head = root
return root
116. Populating Next Right Pointers in Each Node
Given a binary tree
struct TreeLinkNode {
TreeLinkNode *left;
TreeLinkNode *right;
TreeLinkNode *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Note:
You may only use constant extra space.
You may assume that it is a perfect binary tree (ie, all leaves are at the same level, and every parent has two children).
For example,
Given the following perfect binary tree,
1
/ \
2 3
/ \ / \
4 5 6 7
After calling your function, the tree should look like:
1 -> NULL
/ \
2 -> 3 -> NULL
/ \ / \
4->5->6->7 -> NULL
这道题还是比较不直接,下面通过两层while循环,比较巧妙。
class Solution:
# @param root, a tree link node
# @return nothing
def connect(self, root):
if root is None:
return
pre = root
while pre.left:
cur = pre
while cur:
cur.left.next = cur.right
if cur.next:
cur.right.next = cur.next.left
cur = cur.next
pre = pre.left
还一种递归的方法:
class Solution2:
# @param root, a tree node
# @return nothing
def connect(self, root):
if root is None:
return
if root.left:
root.left.next = root.right
if root.right and root.next:
root.right.next = root.next.left
self.connect(root.left)
self.connect(root.right)
两个方法的关键其实就是如何将一个根节点的右子树指向相邻根节点的左子树。也就是下面一步很关键。
if root.right and root.next: # 不能写成 if root.next
root.right.next = root.next.left
上面两种方法本质是一样的,也是递归和循环的相互转换。
117. Populating Next Right Pointers in Each Node II
在116的基础上由完全二叉树,变为一般二叉树。
这个题可以使用BFS。
class Solution:
# @param root, a tree link node
# @return nothing
def connect(self, root):
if root is None:
return
head = root
while head:
prev, cur, next_head = None, head, None
while cur:
if next_head is None:
if cur.left:
next_head = cur.left
elif cur.right:
next_head = cur.right
if cur.left:
if prev:
prev.next = cur.left
prev = cur.left
if cur.right:
if prev:
prev.next = cur.right
prev = cur.right
cur = cur.next
head = next_head
129. Sum Root to Leaf Numbers
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
For example,
1
/ \
2 3
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Return the sum = 12 + 13 = 25.
首先想到的思路就是将树所有的路径遍历一遍,并保存成一个数组。
代码实现为:
class Solution(object):
def sumNumbers(self, root):
"""
:type root: TreeNode
:rtype: int
"""
res = 0
path = self.allpath(root)
for p in path:
res += self.listToint(p)
return res
def listToint(self,path=[]):
sum = 0
for item in path:
sum = sum*10 + item
return sum
def allpath(self,root):
if root is None:
return []
if root.left is None and root.right is None:
# warning not retrurn [root.val]
return [[root.val]]
a = self.allpath(root.left) + self.allpath(root.right)
return [[root.val] + i for i in a]
上面的解法不够简练,参考别人:
# DFS
def sumNumbers(self, root):
self.res = 0
self.dfs(root, 0)
return self.res
def dfs(self, root, value):
if root:
# if not root.left and not root.right:
# self.res += value*10 + root.val
self.dfs(root.left, value * 10 + root.val)
# if not root.left and not root.right:
# self.res += value*10 + root.val
self.dfs(root.right, value * 10 + root.val)
if not root.left and not root.right:
self.res += value * 10 + root.val
# dfs + stack
def sumNumbers1(self, root):
if not root:
return 0
stack, res = [(root, root.val)], 0
while stack:
node, value = stack.pop()
if node:
if not node.left and not node.right:
res += value
if node.right:
stack.append((node.right, value*10+node.right.val))
if node.left:
stack.append((node.left, value*10+node.left.val))
return res
# bfs + queue
def sumNumbers2(self, root):
if not root:
return 0
queue, res = collections.deque([(root, root.val)]), 0
while queue:
node, value = queue.popleft()
if node:
if not node.left and not node.right:
res += value
if node.left:
queue.append((node.left, value*10+node.left.val))
if node.right:
queue.append((node.right, value*10+node.right.val))
return res
130 . Surrounded Regions
Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.
A region is captured by flipping all 'O's into 'X's in that surrounded region.
For example,
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
X X X X
X X X X
X X X X
X O X X
以下是DFS常规解法:
class Solution(object):
def solve(self, board):
"""
:type board: List[List[str]]
:rtype: void Do not return anything, modify board in-place instead.
"""
m = len(board)
if m == 0:
return
n = len(board[0])
if n == 0:
return
for i in xrange(m):
self.dfs(i,0,board,m,n)
self.dfs(i,n,board,m,n)
for j in xrange(n):
self.dfs(0,j,board,m,n)
self.dfs(m,j,board,m,n)
for i in xrange(m):
for j in xrange(n):
if board[i][j] == '1':
board[i][j] = 'O'
elif board[i][j] == 'O':
board[i][j] = 'X'
def dfs(self,i,j,board,m,n):
if i < 0 or i > m or j < 0 or j > n or board[i][j] != 'O':
return
board[i][j] = '1'
self.dfs(i + 1, j, board, m, n)
self.dfs(i - 1, j, board, m, n)
self.dfs(i, j + 1, board, m, n)
self.dfs(i, j - 1, board, m, n)
133. Clone Graph
# Method 1: BFS
# Definition for a undirected graph node
# class UndirectedGraphNode(object):
# def __init__(self, x):
# self.label = x
# self.neighbors = []
import Queue
class Solution(object):
def __init__(self):
self.visited = {}
def cloneGraph(self, node):
"""
:type node: UndirectedGraphNode
:rtype: UndirectedGraphNode
"""
if not node:
return None
newHead = UndirectedGraphNode(node.label)
self.visited[node] = newHead
myQueue = Queue.Queue()
myQueue.put(node)
while myQueue.qsize():
current = myQueue.get()
for neighbor in current.neighbors:
if neighbor not in self.visited:
newNode = UndirectedGraphNode(neighbor.label)
self.visited[current].neighbors.append(newNode)
self.visited[neighbor] = newNode
myQueue.put(neighbor)
else: # turn directed graph to undirected graph
self.visited[current].neighbors.append(self.visited[neighbor])
return newHead
# Method 2: DFS
class Solution(object):
def cloneGraph(self, node):
"""
:type node: UndirectedGraphNode
:rtype: UndirectedGraphNode
"""
if not node:
return None
return self.dfs(node, {})
def dfs(self, node, map):
if node in map:
return map[node]
newNode = UndirectedGraphNode(node.label)
map[node] = newNode
for neighbor in node.neighbors:
newNode.neighbors.append(self.dfs(neighbor, map))
return newNode
作者:Jason_Yuan
BFS解法比较直观,DFS这样的递归一直比较绕,需要多理解理解。
199. Binary Tree Right Side View
Given a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
For example:
Given the following binary tree,
1 <---
/ \
2 3 <---
\ \
5 4 <---
You should return [1, 3, 4].
简单的思路应该是不断递归,并向下传递上一层的度,从右向左遍历。
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def rightSideView(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
lookup = {}
self.dfs(root,0,lookup)
return lookup.values()
def dfs(self,root,level,lookup):
if root:
if level not in lookup:
lookup[level] = root.val
self.dfs(root.right,level+1,lookup)
self.dfs(root.left,level+1,lookup)
if __name__ == '__main__':
root = TreeNode(1)
root.right, root.left = TreeNode(2), TreeNode(3)
s = Solution()
print s.rightSideView(root)
讨论区提供的参考,思路和自己一样,但性能相差不大。
def rightSideView(self, root):
def collect(node, depth):
if node:
if depth == len(view):
view.append(node.val)
collect(node.right, depth+1)
collect(node.left, depth+1)
view = []
collect(root, 0)
return view
200. Number of Islands
Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
11110
11010
11000
00000
Answer: 1
Example 2:
11000
11000
00100
00011
Answer: 3
DFS和BFS的灵活使用问题。
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
m = len(grid)
if m == 0:
return 0
n = len(grid[0])
if n == 0:
return 0
res = 0
for i in xrange(m):
for j in xrange(n):
if grid[i][j] == 0:
continue
res += 1
self.dfs(grid,m,n,i,j)
return res
def dfs(self,grid,m,n,i,j):
if i < 0 or i >= m or j < 0 or j >= n:
return
if grid[i][j]:
grid[i][j] = 0
self.dfs(grid, m, n, i-1, j)
self.dfs(grid, m, n, i + 1, j)
self.dfs(grid, m, n, i, j-1)
self.dfs(grid, m, n, i, j+1)
上面的程序是最基本的DFS,但总是出现问题,递归深度超出限制。
膜拜下别人的程序
def numIslands(self, grid):
def sink(i, j):
if 0 <= i < len(grid) and 0 <= j < len(grid[i]) and grid[i][j] == '1':
grid[i][j] = '0'
map(sink, (i+1, i-1, i, i), (j, j, j+1, j-1))
return 1
return 0
return sum(sink(i, j) for i in range(len(grid)) for j in range(len(grid[i])))
上面程序确实很妙,很简化,厉害。
207. Course Schedule (拓扑排序)(重要)
There are a total of n courses you have to take, labeled from 0 to n - 1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
For example:
2, [[1,0]]
There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.
2, [[1,0],[0,1]]
There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.
这道题的关键就是看这些关联课程有没有形成一个环,如果成了一个环就说明不可能。本质还是一个DFS搜索问题。关键还是问题的描述和建模。
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
if numCourses < 2 or len(prerequisites) < 2:
return True
# prerequisites.sort()
while True:
count = 0
mark = [True] * numCourses
for pre in prerequisites:
mark[pre[0]] = False
for pre in prerequisites:
if mark[pre[1]]:
count += 1
prerequisites.remove(pre)
if prerequisites == []:
return True
elif count == 0:
return False
上面效率比较低
import collections
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
zero_in_degree_queue, in_degree, out_degree = collections.deque(), {}, {}
for i, j in prerequisites:
if i not in in_degree:
in_degree[i] = set()
if j not in out_degree:
out_degree[j] = set()
in_degree[i].add(j)
out_degree[j].add(i)
for i in xrange(numCourses):
if i not in in_degree:
zero_in_degree_queue.append(i)
while zero_in_degree_queue:
prerequisite = zero_in_degree_queue.popleft()
if prerequisite in out_degree:
for course in out_degree[prerequisite]:
in_degree[course].discard(prerequisite)
if not in_degree[course]:
zero_in_degree_queue.append(course)
del out_degree[prerequisite]
if out_degree:
return False
return True
257. Binary Tree Paths
这道题比较简单呀,常规题。
class Solution(object):
def binaryTreePaths(self, root):
"""
:type root: TreeNode
:rtype: List[str]
"""
if root is None:
return []
if root:
if root.left is None and root.right is None:
return [str(root.val)]
a = self.binaryTreePaths(root.left) + self.binaryTreePaths(root.right)
return [str(root.val) + '->' + i for i in a]
332. Reconstruct Itinerary
def findItinerary(self, tickets):
targets = collections.defaultdict(list)
for a, b in sorted(tickets)[::-1]:
targets[a] += b,
route = []
def visit(airport):
while targets[airport]:
visit(targets[airport].pop())
route.append(airport)
visit('JFK')
return route[::-1]
Iterative version:
def findItinerary(self, tickets):
targets = collections.defaultdict(list)
for a, b in sorted(tickets)[::-1]:
targets[a] += b,
route, stack = [], ['JFK']
while stack:
while targets[stack[-1]]:
stack += targets[stack[-1]].pop(),
route += stack.pop(),
return route[::-1]
下面两个程序是神奇,基本上一样输出却不一样
from collections import defaultdict
class Solution(object):
def findItinerary(self, tickets):
"""
:type tickets: List[List[str]]
:rtype: List[str]
"""
ticket_map = defaultdict(list)
for a,b in sorted(tickets)[::-1]:
print a, b
ticket_map[a] += b,
route = []
def visit(airport):
while ticket_map[airport]:
visit(ticket_map[airport].pop())
route.append(airport)
print route
visit('JFk')
return route[::-1]
def findItinerary1(self, tickets):
targets = defaultdict(list)
for a, b in sorted(tickets)[::-1]:
print a, b
targets[a] += b,
route = []
def visit(airport):
while targets[airport]:
visit(targets[airport].pop())
route.append(airport)
print route
visit('JFK')
return route[::-1]
337. House Robber III
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the "root." Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that "all houses in this place forms a binary tree". It will automatically contact the police if two directly-linked houses were broken into on the same night.
Determine the maximum amount of money the thief can rob tonight without alerting the police.
Example 1:
3
/ \
2 3
\ \
3 1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
Example 2:
3
/ \
4 5
/ \ \
1 3 1
Maximum amount of money the thief can rob = 4 + 5 = 9.
class Solution(object):
def rob(self, root):
"""
:type root: TreeNode
:rtype: int
"""
def robHelper(root):
if not root:
return (0, 0)
left, right = robHelper(root.left), robHelper(root.right)
return (root.val + left[1] + right[1], max(left) + max(right))
return max(robHelper(root))
这道题还是要和之前I、II结合起来考虑,都需要考虑当前偷还是不偷,返回一个数组,第一个元素代表偷当前,第二个元素代表不偷。其他思路和之前一样,采用动态规划。
复习 : https://www.youtube.com/watch?v=-i2BFAU25Zk