GraphicsLab Project之Diffuse Irradiance Environment Map

 

作者：i_dovelemon

日期：2020-01-04

主题：Rendering Equation,Irradiance Environment Map,Spherical Harmonic

 

引言

        在实时图形渲染中，Global Illumination 是圣杯级的效果。为了实现这个效果，前辈们开发了很多的技术。但是这些技术大都只能用于静态物体上，对于动态的物体却不能很好的支持。所以，为了让动态的物体也有一点 GI 的效果，开发出了一系列的技术。今天，我们就来介绍其中一种技术：Diffuse Irradiance Environment Map。在游戏开发领域，一般称之为 Light Probe(注：当然 Light Probe 能够实现更多的效果，Diffuse 的 GI 是其中一种)。

        Diffuse Irradiance Environment Map 是基于 Environment Map 来实现的。所以，它不会考虑阴影和模型本身的光照影响。同时，我们也只探讨光照中的 Diffuse 部分，即 Lambert BRDF 部分。

        文章中会存在大量的渲染相关的术语，诸如 irradiance，radiance，solid angle 等等。我们假设你已经了解了这些基础性的概念知识，如果不是，PBRT [文献1] 是一个很好的参考资料。

        本文将主要从两个方面来讲述：一个是传统的计算 Diffuse Irradiance Environment Map 的方法，我们称之为 Brute force；另外一种是基于 Spherical Harmonic 的方法。

 

背景知识

        我们回顾下渲染方程，可以知道一个点在半球范围里面受到的 irradiance 为：

$E(\vec{n})=\int_{\Omega(\vec{n})}^{ }L(\vec{w})(\vec{n}\cdot\vec{w})d\vec{w} \ \ \ \ \ \ \ \ (1)$

也就是说，对于一个固定的 Environment Map (即 $L(\vec{w})$ 相同)来说，irradiance 只和 normal 有关。所以，我们可以通过预计算，将 Environment Map 对应的 Irradiance Environment Map 保存为一个和 normal 相映射的形式，然后通过顶点的 normal 来获取对应的 irradiance 信息。获取到 irradiance 信息之后，带入下面的公式，就能够得到最终需要显示的颜色值：

$B(\vec{p},\vec{n})=f(\vec{p})E(\vec{n}) \ \ \ \ \ \ \ \ (2)$

其中 $f(\vec{p})$ 表示的是 Diffuse 的 BRDF。

 

BruteForce 方法

        公式(1)中计算 irradiance 的方法，是一个在半球范围里面积分的形式，这种方式不存在解析解，没有办法直接去计算得到。但是，由于光照环境是通过 Environment Map 来表达的，我们可以将公式(1)转化为离散的形态，如下公式所示：

$E(\vec{n})=\sum_{i=0}^{N-1}L(\vec{w})(\vec{n}\cdot\vec{w})d(\vec{w})\ \ \ \ \ \ \ \ (3)$

其中，N 表示的是整张 Environment Map 上的所有像素的数量；$L(\vec{w})$ 表示的是在 $\vec{w}$ 方向上的 radiance；$d(\vec{w})$ 表示的是在 $\vec{w}$ 方向上像素的 solid angle。

        这样，我们就有了一个方法来实际计算一个 normal 方向上的 irradiance 的值了。

        我们知道了如何计算一个 normal 对应的 irradiance 的值，那么这个值该怎么保存了？很明显的，我们可以利用另外一张 Cubemap 来保存各个 normal 计算出来的对应的 irradiance 的值，而这个新的 Cubemap 就是 Diffuse Environment Irradiance Map。以下是整个过程的伪代码：

for pixel_iem in IrradianceEnvironmentMap
        n = GetNormal(pixel_iem)
        irradiance = 0
        for pixel in EnvironmentMap
                L = GetRadiance(pixel)
                w = GetRadianceDir(pixel)
                dw = GetTexelSolidAngle(pixel)
                irradiance += L * max(0, dot(n,w)) * dw
        pixel_iem = irradiance

 

Cubemap Texel Solid Angle

　　上面的代码中，唯一可能比较难计算的是：GetTexelSolidAngle。[文献2] 中详细的解释了如何定义这个函数，以及该函数背后的数学原理，这里给出实际的代码，不再赘述：

    private static float AreaElement(float x, float y)
    {
        return Mathf.Atan2(x * y, Mathf.Sqrt(x * x + y * y + 1.0f));
    }

    private static float TexelCoordSolidAngle(float x, float y, int size)
    {
        // Scale up to [-1,1] range (inclusive), offset by 0.5 to point to texel center
        float u = 2.0f * (x + 0.5f) / size - 1.0f;
        float v = 2.0f * (y + 0.5f) / size - 1.0f;

        float invRes = 1.0f / size;

        // Project area for this texel
        float x0 = u - invRes;
        float y0 = v - invRes;
        float x1 = u + invRes;
        float y1 = v + invRes;
        return AreaElement(x0, y0) - AreaElement(x0, y1) - AreaElement(x1, y0) + AreaElement(x1, y1);
    }

        我们知道，solid angle 在整个球上的积分值为 $4\pi$。前面我们将公式(1)转化成了离散的形式，这样就导致所有像素的 solid angle 的总和与 $4\pi$ 存在一定的误差，所以需要进行修正。修正之后的伪代码如下所示：

for pixel_iem in IrradianceEnvironmentMap
        n = GetNormal(pixel_iem)
        irradiance = 0
        totalSolidAngle = 0
        for pixel in EnvironmentMap
                L = GetRadiance(pixel)
                w = GetRadianceDir(pixel)
                dw = GetTexelSolidAngle(pixel)
                irradiance += L * max(0, dot(n,w)) * dw
                totalSolidAngle += dw
        pixel_iem = irradiance * 4 * PI / totalSolidAngle

        好了，至此我们就得到了一张 Diffuse Irradiance Environment Map。在渲染的时候，我们只要通过像素的 normal 来采样 Irradiance Environment Map 就可以得到对应的 irradiance。然后带入公式(2)中，得到最终需要显示的颜色值。

 

To PI or not to PI?

        这里有一个容易引起困惑的地方。我们知道，Lambert 光照模型的 BRDF 如下所示：

$f = \frac{c_{diff}}{\pi}\ \ \ \ \ \ \ \ (4)$

而有游戏开发经验的同学就知道，在游戏里面我们定义 Diffuse 的光照模型如下所示：

$B=c_{diff}*c_{light}*max(0,dot(\vec{n},\vec{w}))\ \ \ \ \ \ \ \ (5)$

这里却没有 $\pi$ 相关的值。这是因为在传统的游戏里面，我们定义的 $c_{light}$ 并不是以光学辐射度的单位来定义的，而是以一种对美术更加友好的定义方式：当一个纯白的 Lambert 表面被一束平行于表面 normal 的光所照射时所呈现的颜色为 $c_{light}$。也就是说，传统游戏开发中定义的 $c_{light}$，实际上是真实光学辐射度单位输入除以 $\pi$ 之后的结果，所以公式(5)中就不存在 $\pi$。

       说这么多的意思是，我们定义 Environment Map 是以真实的辐射度单位来保存的，也就是说在计算最终颜色的时候，我们需要自己除以 $\pi$ 来保证结果的正确性，即将公式(4)带入公式(2)中计算最终的颜色值，即：

$B=\frac{c_{diff}}{\pi}E(\vec{n})\ \ \ \ \ \ \ \ (6)$

这里为了简化 shader 中的计算，我们将 $\pi$ 的计算放在了 Diffuse Irradiance Environment Map 里，即：

for pixel_iem in IrradianceEnvironmentMap
        n = GetNormal(pixel_iem)
        irradiance = 0
        totalSolidAngle = 0
        for pixel in EnvironmentMap
                L = GetRadiance(pixel)
                w = GetRadianceDir(pixel)
                dw = GetTexelSolidAngle(pixel)
                irradiance += L * max(0, dot(n,w)) * dw
                totalSolidAngle += dw
        pixel_iem = irradiance * 4 * PI / totalSolidAngle
        pixel_iem = pixel_iem / PI

关于 $\pi$ 的详细讨论可以参考[文献3]。

 

结果 

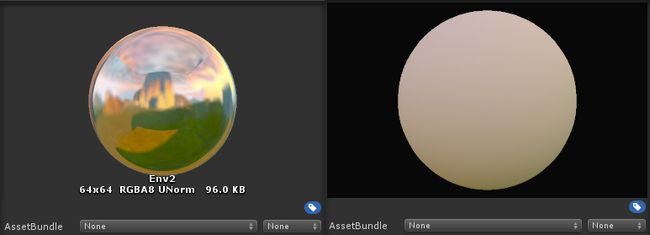
        以下是一些通过 BruteForce 方法计算出来的 Diffuse Irradiance Environment Map 和原始 Environment Map 的对比结果图，Diffuse Irradiance Environment Map 大小是 32x32：

 

 

 

Spherical Harmonic 方法

        Spherical Harmonic 是信号处理里面的一种变换方法。和 Fourier 变换相似，都是将信号转化到频域中去，以此来更加精简的表达原始复杂的信号。不同的是，Spherical Harmonic 更加适合用来处理球面相关的信号。而渲染相关的问题，都是在一个球面范围里面进行，所以选择使用 SH 的方法。关于 SH 的描述，[文献4] 讲解的非常详细，这里就不再赘述。神奇的地方在于，BruteForce 的方法得到的是最终的 Diffuse Irradiance Environment Map，而 SH 的方法得到的是 SH 系数（一般是9个系数）。然后在实际渲染的时候，我们根据这9个系数，重建原始的信号，得到对应的 irradiance。

 

Prefilter

        根据[文献5]中的描述，我们知道如果使用 SH coefficient 的表示方法来编码 Environment Map 的话，将使用如下的公式：

$L(\theta,\phi)=\sum_{l,m}^{ }L_{lm}Y_{lm}(\theta,\phi)\ \ \ \ \ \ \ \ (7)$

而同样的，使用 SH 编码 Irradiance Environment Map 的话，将使用如下的公式：

$E(\theta,\phi)=\sum_{l,m}^{ }E_{lm}Y_{lm}(\theta,\phi)\ \ \ \ \ \ \ \ (8)$

同时定义：

$A=(\vec{n}\cdot\vec{w})$

$A(\theta)=\sum_l^{ }A_lY_{l0}(\theta)\ \ \ \ \ \ \ \ (9)$

根据上面的定义，我们得到：

$E_{lm}=\sqrt{\frac{4\pi}{2l+1}}A_lL_{lm}\ \ \ \ \ \ \ \ (10)$

引入新的变量：

$\hat{A}_l=\sqrt{\frac{4\pi}{2l+1}}A_l\ \ \ \ \ \ \ \ (11)$

将公式(9)(10)(11)带入公式(8)，得到：

$E(\theta,\phi)=\sum_{l,m}^{ }\hat{A}_lL_{lm}Y_{lm}(\theta,\phi)\ \ \ \ \ \ \ \ (12)$

公式(12)中，$\hat{A}_l$是可以预先计算出来的，$Y_{lm}(\theta,\phi)$ 通过带入 normal，也能够计算出来，只有 $L_{lm}$ 是未知的。所以，我们 Prefilter 操作的目的就是计算出 $L_{lm}$ 的值。

        [文献5]中讲述了我们只需要3阶的 SH 系数，就能够很好的表达信号，所以我们只需要计算出来 $l <= 2$ 的 SH 系数即可。

        根据文献[4]中的描述，计算 SH 系数的方式就是将信号投影到对于的基向量上去即可，即：

$L_{lm}=\int_{\Omega}^{ }L(\vec{w})Y_{lm}(\vec{w})d(\vec{w})\ \ \ \ \ \ \ \ (13)$

同样的，我们将这个积分形式的方程，转化为离散的形式[文献6]，如下所示：

$L_{lm}=\sum_{i=0}^{N-1}L(\vec{w})Y_{lm}(\vec{w})d(\vec{w})\ \ \ \ \ \ \ \ (14)$

这样，我们就能够通过计算，得到3阶球谐的9个系数。但是我们知道光的单位是有RGB三个部分组成，每一个部分可以单独的进行 SH 系数的求解，所以最终的结果是9个RGB系数。以下是求解这些系数的伪代码：

foreach sh_coefficient
        sh_coefficient = 0
        totalSolidAngle = 0
        for pixel in EnvironmentMap
                L = GetRadiance(pixel)
                sh = GetSHBais(pixel)
                dw = GetTexelSolidAngle(pixel)
                sh_coefficient += L * sh * dw
                totalSolidAngle += dw
        sh_coefficient = sh_coefficient * 4 * PI / totalSolidAngle

计算过程十分简单，唯一需要注意的点是GetSHBais 函数的实现。这个函数的定义可以通过预先计算得到，如下所示[文献5]：

 

至此，Prefilter 的工作就完成了。 

 

Rendering

        通过公式(12)，我们在知道了 SH 系数的情况下，就可以重建原始的 irradiance 信号。由于公式(12)中只有 $L_{lm}$ 是未知的，其他两个部分都是可以通过预计算得到，所以合并预计算的部分，我们得到根据 SH 系数重建信号的公式[文献5]：

 

         这样，在知道了 irradiance 的情况下，带入到公式(2)中，得到：

$B=\frac{c_{diff}}{\pi}E\ \ \ \ \ \ \ \ (15)$

 

结果

        以下是通过 SH 的方法得到的 Diffuse Irradiance Environment Map 和原始 Environment Map 的对比：

 

 

 

 

两种方法对比

        我们假设原始 Environment Map 的尺寸是 NxNx6，而 BruteForce 方法计算得到的 Diffuse Irradiance Environment Map 的尺寸为 MxMx6，那么对于 BruteForce 的方法来说，就是一个 O(NxNxMxM) 的操作。而对于 SH 方法来说，它的计算时间为 O(9xNxN)。两个方法在Prefilter上面，SH 的速度大大提高。同时，对于 BruteForce 方法来说，得到的结果是一张 Cubemap，在渲染的时候需要进行采样，而 SH 的方法则是通过一些简单的计算得到最终的结果。

        以下是两种方式得到的 Diffuse Irradiance Environment Map 的对比：

 

 可以看到，通过 SH 方式得到的结果和 BruteForce 的方法得到的结果误差非常小。

 

结论

        如果在实际使用过程中，你需要使用 Diffuse Irradiance Environment Map，也是建议通过先求 SH 系数，然后重建 Diffuse Irradiance Environment Map，这样的方法比 BruteForce 来计算得到 Diffuse Irradiance Environment Map 的速度要快的多。

        当然除了这里提到的方法，还有很多其他的方法来计算 Diffuse Irradiance Environment Map，比如[文献7]中，使用 Rieman 积分的方式，加速 BruteForce 方法来得到结果。

        这里只是介绍了基础的知识，在实际项目开发过程中还需要处理诸多的问题，比如：Light Probe Auto Layout，Light Probe Blend 等等复杂的问题，后面有机会会专门讲解这方面的知识。

        本文的配套代码可以在这里获取得到：https://github.com/idovelemon/UnityProj/tree/62eff639347645f380d651dd80b8720010f6097b/IrradianceEnvironmentMap。值得注意的是，学术界对球面坐标系的定义是 Z 轴朝上，而在 Unity 里面是 Y 轴朝上，实际代码实现的时候需要转化下方向。

 

参考文献

[1] Physically Based Rendering : From Theory to Implementation

[2] Cubemap Texel Solid Angle

[3] PI or not to PI in game lighting equation

[4] Spherical Harmonic Lighting:The Gritty Details

[5] An Efficient Representation for Irradiance Environment Maps

[6] Real-Time Computation of Dynamics Irradiance Environment Maps

[7] GraphicsLab Project 之 IBL - Diffuse 光照