冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外,似乎没有什么值得推荐的。--by Donald E. Kunth
冒泡排序的基本思想:每次比较两个相邻的元素,如果他们的顺序错误就把它们换过来。
例如把一组数字(1,3,5,2,7,8,4,6,9)从小到大排序。
根据基本思想
先让1和3比较,1<3不用交换(1,3,5,2,7,8,4,6,9)
然后3和5比较,3<5不用交换(1,3,5,2,7,8,4,6,9)
然后5和2比较,2<5交换位置(1,3,2,5,7,8,4,6,9)
然后5和7比较(1,3,2,5,7,8,4,6,9)
然后7和8比较(1,3,2,5,7,8,4,6,9)
然后8和4比较(1,3,2,5,7,4,8,6,9)
然后8和6比较(1,3,2,5,7,4,6,8,9)
然后8和9比较(1,3,2,5,7,4,6,8,9)
到此完成一轮比较共比较了八次(元素总数减一次)
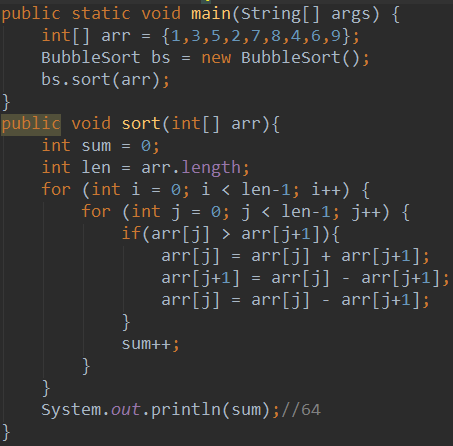
重复以上步骤即可完成排序,代码如下(图bubbleSort00)
这是粗暴的实现了基本思想,其中有可以优化的地方
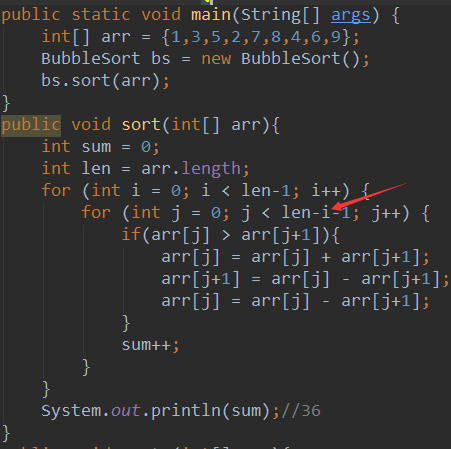
1、当一次循环以后就找到了最大的元素所以在下一次循环的时候就可以不用再比较了,代码如下(图bubbleSort01)
2、另一种情况可能在某一次循环结束后就已经排好了则不需要再对剩余的元素循环比较了(最极端的情况就是所有元素初始状态就是排好序的),所以我们可以加一个变量来记录本次循环是否有交换数据的情况,如果没有则说明已经排好序。代码如下(图bubbleSort02)
时间复杂度:
可以看出如果元素最开始有序只需一次循环就可以搞定,所以最好的时间复杂度为O(n)。
不凑巧如果需要循环所有元素比如初始是反序的状态,即时间复杂度为n(n-1)/2=O(n²)
算法稳定性:
可以看出排序过程中只有不相等的时候才会出现交换元素的情况,所以排序算法是稳定的。