全书章节:
Preface
Part 1. Linearity
Part 2. Inference
Part 3. Expectation
Part 4. Regression
Part 5. Existence
Preface
大众一直对学习数学有什么用感到困惑,似乎生活中很少会用到抽象的数学公式,但更重要的是学习数学思维。如下面这个故事:
在二战期间,The Statistical Research Group (SRG) 为战时的美军服务,他们面对的问题是,既要武装战机,又不想让战机过于沉重影响其灵活性,那么就要武装最重要的部位,而舍弃其他。他们发现,返回的机身上发动机上弹孔最少,而主机身的弹孔最多。SRG 的官员认为,如果把有限的武装用在弹孔最多的地方,会提升战机的效能。但当他们把这个问题抛给 Abraham Wald (著名数学家)以后,他给出的答案却超出了大家的想象。他认为武装最应该用于弹孔最少的部位,即发动机,因为那些发动机中弹过多的飞机,根本就没有机会安全返回。
这就好像你在医院的术后恢复室里看到的病人,更多的是腿部中弹而非胸部中弹。那是因为胸部中弹的人很难康复。
上面这个故事中可以用上一个古老的数学方法:把某一变量设为零。在上面的例子中,就是把一架飞机发动机中了一弹后还能继续飞行的概率设为零。这意味着一架飞机一旦发动机中弹,就会坠毁。于是当你看到,返回的飞机机身上布满了弹孔,唯独发动机上没有弹孔。现在你有两种解释方法:一是德国的子弹正好打到机身的各个部位,除了发动机;二是发动机是整架飞机最脆弱的部分。这样看来,第二种解释更合理。
为什么 Wald - 这一不懂任何空中战斗的数学家,会比美军官员更能看到问题的本质?这就要提到他的数学思维。数学家永远会问:你的假设是什么?它被证实过吗?在上面的故事中,官员的假设是:返回的飞机是所有飞机中的随机取样。如果真是这样,你就可以通过观察返回的飞机机身上弹孔的分布来决定怎样武装战机。一旦你意识到你在做这样的假设,你就很容易发现它根本就是错的。你很难相信,不管哪个部位中弹,飞机存活的概率都相同。
Wald 的另一优势是他的抽象思维。上面的整个故事在他眼里就是幸存者偏差(survivorship bias)。正如在共同基金(mutual funds)的评判中,如果你直接计算十年内的平均增长率,你可能会得出很大的数字。但你忽略了那些退出共同基金的基金。在十年中,有些基金出现了,有些消失了。如果你只计算那些在十年后还存在的基金,那么与只计算那些安全返回的飞机机身上的弹孔没什么两样。如果你找不到一架中弹超过两次的飞机,这代表什么?这不代表飞行员能够安全避开子弹,而是那些中弹两次的飞机都坠毁了。
说到这里,我们应该知道,数学就是用其他的方法来延伸常识。尽管真正的数学家在解决问题时,会用到复杂的公式。但普通人不需要掌握复杂的公式,而要了解其背后的思想。如我们很小的时候学习的加法交换律和乘法交换律。它们是这样,不是因为书本告诉我们要这样做,而是因为它就是事实。12 个苹果分成 5 个和 7 个,或者 7 个和 5 个,其总和都是 12 个苹果,而不会变成 11 个或 13 个。下图排列的 12 个小孔,当你横着看时是4×3 个小孔,当你把脑袋偏向左边 90 度看时,就变成了 3×4 个小孔,但不管你从什么角度看,它都是 12 个,这一点不会变。
o o o o
o o o o
o o o o
如果说数学可以分成四个象限
简单,深刻 复杂,深刻 简单,浅显 复杂,浅显
那么,本书中的数学就处于左上角的象限,就是要教你用简单的数学对各种现象产生深刻的理解。
Part 1. Linearity
1. Less like Sweden
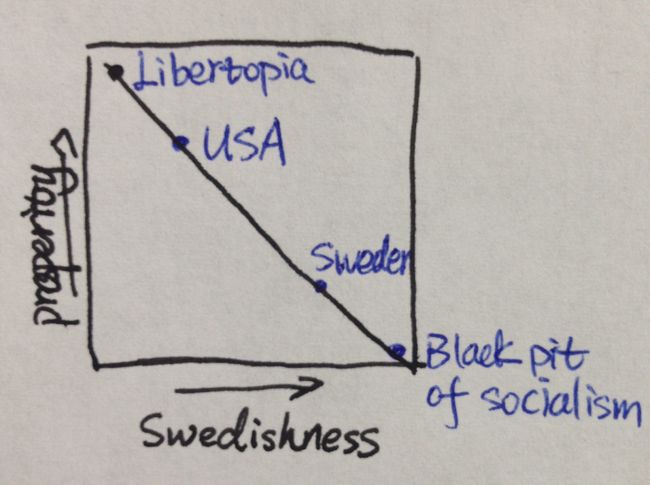
几年前,当奥巴马开始推行全民医保时,Daniel J. Mitchell 就问:“为什么当瑞典在试图变得更不 ‘瑞典’(less like Sweden) 时,奥巴马却力图使美国变得更 ‘瑞典’ 呢?”
这个问题提得好,该问题的提出是基于以下的假设:社会的繁荣程度和它 ‘瑞典’ 化的程度呈反向线性关系,如下图:
但实际上是否如此呢?有另外一种观点认为它不是一种线性关系,而是非线性关系。
这样看来,以上 Mitchell 的推理就是错误的线性关系(false linearity)。
这种非线性关系被称为拉弗曲线(Laffer curve)。他在 1974 年与别人在餐馆吃晚饭聊到政府收入与征税率之间的关系,于是在餐巾纸上画下这样的图:
当税率为零时,政府当然什么也得不到;但当税率为 100% 时,也没有人会愿意工作,让所有的劳动果实都归政府所有。只有当税率适当时,政府收入才可能最高。那么问题的关键就是找到我们所处的位置,这决定了我们需要如何改变。有的人认为现在的税率太高了,应该降低税率;也有的人认为税率还不够高。我们无法仅凭这张图就确定我们处于什么位置。
当然,政府收入和税率之间的关系不是线性的,但也不一定就如 Laffer curve 所显示的那样,是个完美的抛物线,它可能是下图中的任何一条线,或者更复杂。但它指出了,当降低税率时,政府的收入有可能升高。但不能因为有这个可能,并且你希望在降低税率时,政府的收入能够提高,而认为,当降低税率时,政府的收入一定会升高。
另外,政府的收入达到最高,并不是我们所追求的。如何合理分配政府的收入,是个更重要的问题。
2. Straight locally, curved
这一章讲述了数学上的无理数、积分和柯西数列的来源。一个圆整体来看是曲线,但如果放大到足够大,局部也可能近似直线。就好像我们站在地球上,感觉脚下是平地,但其实从太空看,地球表面其实是曲面。
3. Everyone is obese
线性回归(linear regression)是使用非常广泛的数学工具,但要注意使用前提。一段抛物线,如果看整体,它是曲线;但如果放大到足够小,也可以看成直线。所以在使用线性拟合时,要注意使用范围,不能延伸到无限。
有研究表明,到 2048 年,所有的美国人都会患上肥胖症,其根据是下图的几个点。
如果用线性回归来分析,就是下图。
然而真实情况可能是,肥胖症随时间的变化并不是线性的,它可能是下图这样的。
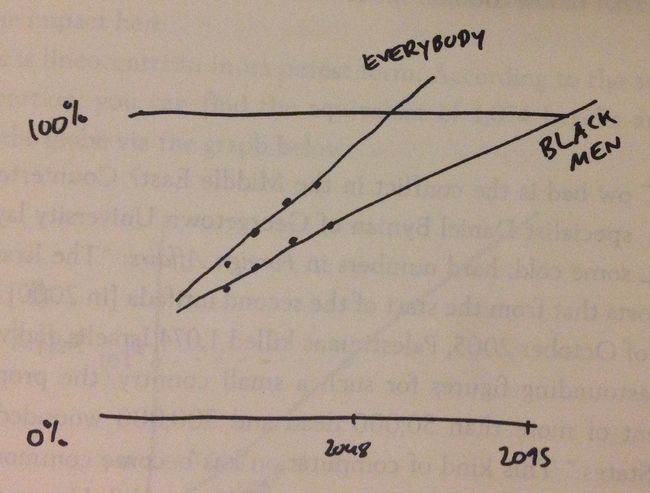
另外有研究表明,美国黑人患肥胖症的比例要低于整体美国人中患肥胖症的比例。如果按照线性回归来分析,一直到 2095 年,美国黑人才会全体患上肥胖症。到 2048 年,当全体美国人都患上肥胖症时,只有 80% 的美国黑人会患上肥胖症,这岂不荒谬?
综上所述,在做线性回归分析之前,要先分析这样做是否符合常理。
4. How much is that in dead Americans?
当世界上某地发生不幸,产生一些受害者时,我们喜欢把它换算成美国人。如在 2000 年和 2005 年十月之间,有 1074 名以色列人被杀害,有 7520 名受伤。如果换算成美国人,就相当于超过 50000 人死亡,和超过 300000 人受伤。这里面的逻辑是,看受害者人数占以色列总人口的比例,乘以美国总人口,就得出相应的数据。然而这样换算真的对吗?
这里有一种数学思维可以帮助分析这类计算:当你在实际中运用一种数学方法时,尝试从不同的角度来分析同一件事。如果你得出了几个不同的答案,那么就要小心了,你所使用的数学方法可能有问题。
例如:发生在 2004 年马德里的阿托查(Atocha)火车站的爆炸造成了 200 人死亡。如果爆炸发生在纽约中央火车站,会造成什么结果?美国总人口是西班牙的 7 倍,200 人约占西班牙总人口的 0.0004%,于是相当于美国的 1300 人。换一种思路,200 人是马德里人口的 0.006%,纽约市人口是马德里的 2.5 倍,于是相当于 463 名受害者。如果把马德里州与纽约州相比,则相当于 600 人。我们到底应该相信哪一种算法呢?
当然,也不能完成否认比例的作用。如果你想知道美国的哪个地方患脑癌的比例最高,你不能只看患脑癌人数最多的州:加州,德克萨斯,纽约和佛罗里达,因为这些地方人口最多。那么更好的方法是看比例。其中比例最高的州是南达科他州、内布拉斯加、阿拉斯加、特拉华和缅因州,而比例最低的是怀俄明、佛蒙特、北达科他、夏威夷和哥伦比亚特区。为什么相邻的南北达科他州、佛蒙特和缅因差距这么大?
有一个答案:因为上榜的十个州有一个共同特点为,全都人烟稀少。但是为什么人口少就会出现这样的情况呢?这就要提到大数法则(the Law of Large Numbers)了,即当一个实验重复的次数越多,你得到的结果就越趋于一个固定的平均数。反过来讲,当重复的次数很少时,你得到的数据就会有很大的波动。在这里就表现为,当一个州的人口特别少时,其患脑癌的比例就比较容易出现极大或极小值。
另外,基数越大时,其偏离真实值的幅度大概与基数的根号值相当。当你扔硬币时,有 50% 机率扔到带花的一面,当你扔 10 次时,扔到花的次数与 5 次的偏差大概在 3 左右(根号 10 大约为 3);扔 100 次时,大概在 10 左右(根号 100 为 10);扔 1000 次时,大约为 31 (根号 1000 大约为 31)。因此,当你在 100 里有 60 次扔到花时,它与 50-50 的真实值相差 10,等于根号 100。而当你在 1000 里有 538 次扔到花时,它与 500-500 真实值相差 38,这比根号 1000 还要大,因此,尽管两次的比例中(60% 和 53.8%),前者比例大,但后者的结果更反常。这就带出了钟形曲线(Bell curve)或正态分布,即长期来看,与 50-50 的偏差符合正态分布,偏差越大,其出现的几率就越小。
有一件事大家容易误解。如果你扔硬币连续扔出 10 个花,那么第 11 次会出现什么呢?假设硬币没有被做手脚,那么下一次扔出花的几率仍然是 50%!因为硬币没有记忆,它不会因为你之前连扔出 10 个花,下一次就不出现花了。如果你接下来再扔 1000 次硬币,那么在总的 1010 次里,扔出花的比例很可能会接近 50%。这并不是因为后来扔的硬币平衡了之前连续出现的 10 个花(出现花的几率更小),而是因为后面的新数据稀释了之前的数据,使之前连续出现的 10 个花变得不那么重要了,甚至可以忽略不计。
5. More pie than plate
当牵涉到负数时,不要谈论百分比。例如,我这个月卖咖啡损失了 500 元,而卖蛋糕盈利 750 元,卖 CD 盈利 750 元,总盈利 1000 元,那么我可以说卖蛋糕的盈利占总盈利的 75%,同样我也可以说卖 CD 的盈利占总盈利的 75%。于是你就发现,这两个比例加起来超过了 100%。但如果你只提到卖蛋糕的盈利占比 75%时,不了解内情的人可能以为你的大部分盈利来自卖蛋糕,而实际上你卖蛋糕和卖 CD 的盈利和盈利占比相同。
用一个数除以另一个数是计算,而弄清楚你应该用哪个数除以哪个数是数学。
Part 2. Inference
6. The Baltimore stockbroker and The Bible Code
本章讲述了两个类似的故事,说明极不可能发生的事(如百万分之一的概率)实际上经常发生,只要样本足够大。
7. Dead fish don't read minds
紧接着上一章,还是讲到当基数足够大时,极小概率事件也很有可能发生,所以我们不能只看那些发生的事,而忽略了更多没有发生的事。还提到了概率学上很重要的一个概念:null hypothesis(零假设)。书中举了两个例子,第一个例子是,如果我说我有超能力,能把太阳从地平线下拉起来,你每天早上都能看到太阳升起,于是这就证明了我有超能力。不,我们都知道这称不上是证据。但如果我能让太阳不出现,并且太阳真的没有在通常的时间升起,那才算是我有超能力的证据。
第二个例子是,假如我在研发一种新药,做了一组实验,实验组和对照组各 50 名病人,实验组吃我的新药,对照组吃安慰剂。实验完成后发现,实验组的病人比对照组的死亡率更低,于是我说我的药对这种病有效果。不,这其实称不上是新药有效的证据。假如 null hypothesis 为每名病人的死亡率都是 10%(也就是存活率为 90%),但这并不意味着实验组和对照组各会有 5 (50 × 10% = 5)名病人死亡。通过计算得出,实验组与对照组有相同人数的病人死亡的概率是 13.4%,实验组比对照组死亡病人人数多的概率是 43.3%,实验组比对照组死亡病人人数少的概率是 43.3%。我们看到,实验组比对照组死亡病人人数少的概率其实不低。只有当实验组病人死亡人数远比对照组低时,才能说这种新药有效。多低才算低呢?假如对照组有 5 名病人死亡,而实验组没有一个人死亡,我们来计算一下发生这种事的概率。0.9 的 50 次方是 0.00515,这个数字很低。与什么相比很低呢?这里就要提到 p 值,通常 p 值取 0.05,如果在 null hypothesis 的情况下计算得出观察到的现象出现的概率比 p 值低,我们就说排除了零假设。在这个例子里,0.00515 < 0.05,这说明这种新药是有效的。
In common language, 'significance' means something like "important" or "meaningful". But the significance test that scientists use doesn't measure importance. When we're testing the effect of a new drug, the null hypothesis is that there is no effect at all; so to reject the null hypothesis is merely to make a judgement that the effect of the drug is not zero. But the effect could still be very small - so small that the drug isn't effective in any sense that an ordinary non-mathematical Anglophone would call significant.
以上这段话完美解释了什么是零假设和 p 值,以及它们存在的意义。当一个结果通过了 p 值的检验,也只能说这一结果是 "statistically noticeable" 或者 "statistically detectable",而不是 "statistically significant"!因为如果事件出现的概率极低,就算翻倍也算不了什么。如 1995 年英国药管局发布一项警告,说有些避孕药会使人患上静脉血栓的概率增大到吃另外一些避孕药的人的两倍。这一警告使英国出现了一波婴儿潮和流产潮。1996 年比 1995 年多出了 26000 例受孕和 13600 例流产。但实际上吃一代或二代避孕药的人患上静脉血栓的几率为 1:7000,使用新药的人患上静脉血栓的几率为之前的两倍,也就是 2:7000。虽然增大到两倍,该几率仍然很小,因为一个小数的两倍还是小数!
另外,对比两个数据时,其前提可能不同。如有研究发现,在家里被照顾的婴儿比在育儿中心被照顾的婴儿,死亡率要高出 7 倍,也就是 1.6:100000 和 0.23:100000。但是大家不要忽略一个前提,育儿中心一般离家比较远,而每年在车祸中丧生的婴儿有几十例。如果你在路上花了太多时间,那么很可能婴儿的死亡率会比在家里更高。
8. Reductio ad unlikely
验证一个假设是否为真,有一个很简单的方法,也就是假设零假设为真:
- 假设 A 假设是真的
- 如果 A 假设是真的,那么 B 不可能为真
- 但 B 是真的
- 因此,A 假设是假的
举例来说,如果有人说 2012 年华盛顿特区有 200 名儿童死于枪击,而你在网上找不到证据证明这句话是真的还是假的。如果假设这句话是真的,那么 2012 年华盛顿特区发生的杀人事件不会少于 200 例。但事实上就是少于 200 例,因此前面那句话就是假的。
9. The international journal of haruspicy
2005 年一个名叫 John Ioannidis 的人发表了一篇文章:"Why most published research findings are false"。其文章的理论是,科学家只发表那些通过了 p 值检验的结果,而剩下的压根没提。这就好像在第一章的飞机中弹的例子中,只计算了返回的飞机,而没有计算没有返回的。科学界应该允许大家发表没有通过 p 值检验的结果,因为 0.05 的 p 值是规定的数值,而不是一个正确的数值,我们同样可以把 p 值规定为 0.1 或 0.01。
概率是帮你作决定,而不是回答具体问题。科学研究中,能否重复是个很重要的指标。对于任何研究,你都不能死板地使用一个规则或一个公式来判断结论是否正确,永远要具体问题具体对待,因为你对每件事的想法不同,得到的证据也不同,这就牵涉到贝叶斯定理。
10. Are you there, god? It's me, Bayesian inference
当考虑一件事发生的概率时,一个有用的方法是贝叶斯推断(Bayesian inference)。它强调你要先有一个先验概率(prior probability),这个概率不是客观的,而是你主观上在多大程度上相信一件事会发生。另外书中还提到一点,当考虑这个世界上是否存在神时,你不能只考虑存在和不存在,还要考虑存在多个神,或这个世界是个虚拟世界,等等。否则,你很可能得到错误的结论。还有一个有意思的现象,当你让一个人从 0 和 9 中随机挑出一个数时,你很可能会挑 7,若从 1 到 20 中挑出一个数时,很可能会挑 17。相反,很少有人会选以 0 或 5 结尾的数,因为人们潜意识中认为这样的数看起来不像是随机选择的,但实际上这些数和以 7 结尾的数出现的概率相同!在 2009 年伊朗的总统选举中,有人怀疑有选票造假,但没有人能够证实。后来哥伦比亚大学的两名研究生,想到了一个方法。他们找到候选人的支持选票数,按照常理,这些选票数的最后一位数应该是随机的,因此从 0 到 9 每个数字出现的概率都应该接近 10%。但现实不是这样,他们发现了很多个位数为 7 的选票数,差不多是正常概率的两倍,很像是人为写下的数字。虽然这不能作为直接的证据,但指出了一个方向。
Part 3. Expectation
11. What to expect when you're expecting to win the lottery
当买彩票时,或做任何一件事时,你计算的期望值并不是你所期望的。“期望值”这个词会让人产生误解,实际上它代表的是一个平均值,即如果我重复做一件事千百次,它会产生的平均值大概是多少。如果某件事我只做一次,那期望值没有多大用处。用在买彩票上,如果你只买一张彩票,你极大可能会什么也得不到,但如果你买上几万张或几十万彩票,你赢得大奖的概率就高出很多,这时期望值就派上用场了。本章讲述了一些人利用这一规律,把买彩票作为谋生的工具,赚了很多钱。
文中还插入了一个小故事,当你面对一个难题时,如果不能直接解答,你有两个努力的方向,一个是把问题简化,这一方法通常很有效,但有时你还可以把问题复杂化,或者说普遍化或抽象化,得到一个更普遍的解法,或把问题转移,这种方法有时候也会奏效。
12. Miss more planes!
如果你从未错过过一次飞机航班,那么你很可能在机场度过了太长时间。这一章讲了效能(utility)的问题。拿搭乘飞机来说,假设如果你提前 2 小时到达机场,有 2% 的概率会错过航班;若提前 1.5 小时,有 5% 的概率误机;若提前 1 小时,有 15% 的概率误机。假设若错过飞机,会减少 6 个小时的效能,那么以上的三种选择,每种选择带给你的总效能就分别为:-2 + 2% × (-6) = -2.12; -1.5 + 5% × (-6) = -1.8; -1 + 15% × (-6) = -1.9。若作一条效能随到达机场时间的曲线,就如下图,总有一个时间会让效能达到顶点。这也是一条拉弗曲线。
但在使用效能理论时,也要小心。例如,假设一个瓮中装有 90 个球,你只知道其中有 30 个红球,剩下的 60 个里有黑球也有黄球。现在做这样一个实验:
红:如果下一个从瓮中取出的球是红色的,你就得到 100 美元,否则你什么也得不到;
黑:如果下一个从瓮中取出的球是黑色的,你就得到 100 美元,否则你什么也得不到;
非红:如果下一个从瓮中取出的球是黑色或黄色的,你就得到 100 美元,否则你什么也得不到;
非黑:如果下一个从瓮中取出的球是红色或黄色的,你就得到 100 美元,否则你什么也得不到。
相比之下,你更愿意选择 “红” 还是 “黑”?“非红” 还是 “非黑”?
Ellsberg 测试了很多人,他发现大多数人倾向于选择 “红” 或 “非红”,而不是 “黑” 或 “非黑”。因为选择 “红” 或 “非红”,你知道你赢的概率是确定的。
现在换个玩法,假设你要从以上的选择中同时选择两个,要和选 “红” 和 “非红”,要么选择 “黑” 和 “非黑”。如果在上一个实验中你更倾向于选择 “红” 或 “非红”,而不是 “黑” 或 “非黑”,那么合理地推测,这次你也会更愿意选择 “红” 和 “非红”,而不是 “黑” 和 “非黑”。但是,实际上,选择 “红” 和 “非红” 和选择 “黑” 和 “非黑” 结果一样!为什么会这样呢?
这里涉及到 “已知的未知” 和 “未知的未知”。 “已知的未知” 就像 “红”,我们不知道哪一只红球会被选中,但我们能够知道红球出现的概率。而 “黑” 就是 “未知的未知”,我们不仅不知道哪只球是黑色,我们也不知道黑球出现的概率。在决策理论中,前者的未知被叫作 “风险”,而后者的未知被称作 “不确定性”。前者可以被定量分析,而后者却不在数学分析的范围内。
13. Where the train tracks meet
这一章提到的问题很有意思,代数或概率问题有时可以和几何联系起来。还是讨论买彩票的问题,有两种方式买彩票,一种是让电脑随机选,一种是人为挑选号码,两种方法产生的期望值相同,那么为什么还要费那么多时间精力人工填写号码呢?
现在假设有两种选择摆在你面前,一种是直接拿 5 万美元,另一种是你有 50% 的可能失去 10 万美元,有 50% 的可能得到 20 万美元,你选哪一个?大多数人会选择前者,因为后者的风险大,赢和输带给你的效能不同。假如你输了,你很可能没有本钱再来一次,尽管长期来看,你的平均盈利还是 10 万美元。
为了讨论的方便,现在假设彩票由从 1 到 7 的 7 个数字组成,其中的三个数字是特别号码,如果这三个数字全对,你就可以得大奖,若这三个数字你猜对了两个,也可以得小一点的奖。从 这 7 个数字中选出 3 个数字的组合,一共有 35 种可能。现在假设特别号码是 1,4,7,那么经过计算,你猜中两个特别号码的期望值是 2.4。如果手动填写数字,其期望值也是 2.4。但是,后者的方差要小得多。
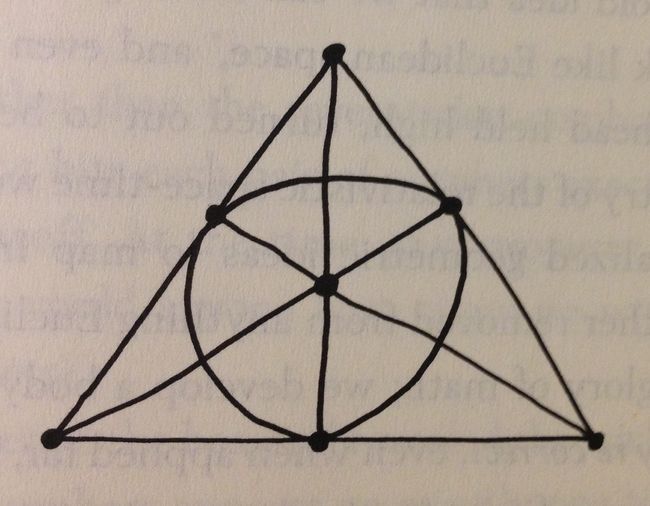
随后,作者由画画中的投射平面引出空间三维点线面的关系,随后提到了一个图形,如下图,它满足两个条件:
- 每两个点只同时出现在一条线中;
- 每两条线只有一个交点。
如果给图中的 7 个点标上数字,如下图,它被叫作 Fano plane。如果把图中的七条线上经过的数字写下来,就是:
124, 135, 167, 257, 347, 236, 456
这与前面提到的彩票游戏完全是一个问题!
在信息传输中有个问题,假设用 0 和 1 来传输信息,如 1110101...,如果其中有一个信号出错了,如果是用在航空卫星中,那么后果可能会很严重。于是人们想到一个办法,就是重复一遍信息,变成 11 11 11 00 11 00 11,于是当意外出现时,如信号变成 10 11 11 00 11 00 11,你就知道有信号出错了,但到底第一个信号应该是 11 还是 00 呢?你还是不清楚。于是人们想到,可以重复两遍信息,于是以上的信息就变成 111 111 111 000 111 000 111,当信息变成 101 111 111 000 111 000 111 时,你就知道很有可能第一个信号是 111。这种编码叫作纠错编码。
但是把信息重复两遍需要消耗很多时间,如果你想即时得到信息,这种方法就不适用了。这时有人想出了一种更便捷的方法,叫作汉明码(Hamming code)。它是把三位数的信号转变成七位数的编码,其编码如下:
000 -> 0000000
001 -> 0010111
010 -> 0101011
011 -> 0111100
101 -> 1011010
110 -> 1100110
100 -> 1001101
111 -> 1110001
接收端只接收八位数的编码,如果中间出错了,假如你收到了 1010001,这不在编码书上,你知道一定有什么地方出错了,对比编码书以后,你发现这个信息与 1110001 只差一个数字,其他的编码都有至少两个以上的数字与接收到的编码不同,从而很可能你接收到的编码实际上是 1110001,而不太可能是其他的编码。
你可能觉得这是个巧合,但它其中蕴含了数字的规律。还是回到买彩票上,如果把 Fano plane 上的七组数字用一个七拉数的编码表示,用 0 代表点在线上,用 1 代表点不在线上,那么 124 就可以表示成 0010111,135 就可以表示成 0101011。我们发现这两组编码都出到在汉明码中。实际上 Fano plane 上的七组数字都可以表示成汉明码。
同样的,在真实的彩票游戏中,你要从 1 到 48 的 48个数字中选出 6 个。Denniston 写下了 285384 种 6 个数字的组合,以下面这些组合开始:
1 2 48 3 4 8
2 3 48 4 5 9
1 2 48 3 6 32 ...
你发现头两张彩票有四个数字相同:2,3,4,48。但是 Denniston 系统的奇妙之处在于,你不会在 285384 张彩票中找出两张有 5 个数字相同的彩票来。我们可以把他的系统转化为一串由 1 和 0 组成的 48 位的数字串,于是第一张彩票就变成:
000011101111111111111111111111111111111111111110
于是,没有两张彩票有 5 个相同的数字就意味着,没有哪两个数字串可以由距离小于 4 的汉明码分开。实际上,每 5 个数字的组合只出现在一张票上。如果你小心选择数字,你可以得到与用电脑随机选择数字相同的期望值,而且风险更小。
以上都是从数学的角度谈论彩票,也可以从别的角度考虑这件事。有的人买彩票并不只是为了赢得大奖,可能他买彩票只是为了一个简单的快乐,可以有一份小小的期待。实际上,如果你去创业,有很大可能失败,这与你买彩票中大奖的概率可能差不多,但从道德层面来讲,创业比赌博好得多。但我们评价一件事,并不只从盈利出发。毕竟,创业时,你实现梦想的过程,甚至是为实现梦想所作的努力,它本身就是一种奖励。
Part 4. Regression
14. The triumph of mediocrity
Secrist 发现,表现最好的公司会逐渐表现得不太好,而表现不好的公司则会逐渐表现得更好,这两种公司都在往中间靠拢。实际上,这不仅发生在生意场上,几乎生活中任何涉及随机变动的事情都可能受到这种回归影响。
15. Galton's ellipse
另一个例子是父子的身高的相关度,Galton 发现,父子的身高有一定的相关性,但也受到一些随机变量的影响。换言之,高挑的父亲的儿子仍然比普通人高,但比父亲稍矮,而矮个子的父亲的儿子仍然比一般人矮,但比父亲稍高。
若把每一个点看作是从原点出发的向量,如果两个向量正交,说明这两个向量没有相关性。但是向量和向量之间不具有传递性,即如果向量 1 和向量 2 相关,向量 2 和向量 3 相关,那么向量 1 和向量 3 相关吗?不一定,见下图,1 和 3 完全有可能正交。
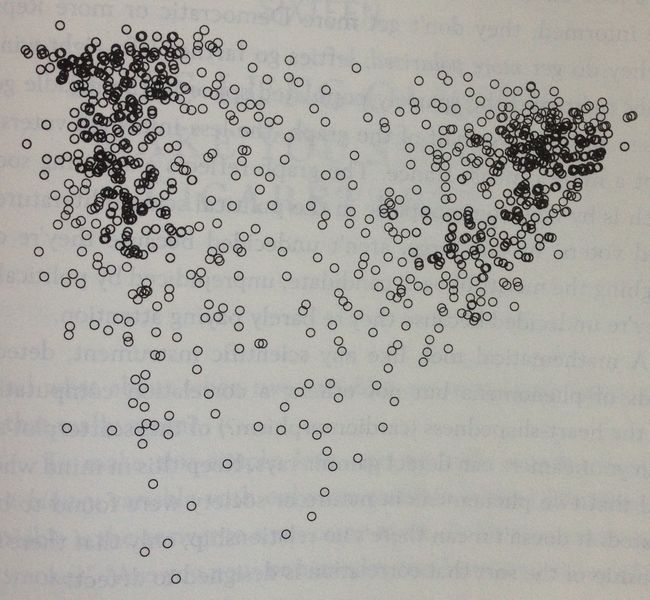
另外,两个变量 uncorrelated 不意味着它们 unrelated (不知道怎么翻译这两个词)。比如在下图中,横坐标代表人们的政治倾向,越靠左越倾向民主党,越靠右越倾向共和党,纵坐标代表人们的知情情况,越靠下越容易回答 “不知道”。显然,横纵坐标代表的变量并没有表现出相关性(uncorrelated),但是它给出了别的信息,即选民了解的情况越深,越两极化,而那些不怎么关心政治的人,想法则更中庸。这些信息是无法从相关性上体现出来的。
16. Does lung cancer make you smoke cigarettes?
很多研究发现了患肺癌和吸烟之间存在相关性,但究竟是吸烟导致了肺癌,还是由于某种未知的原因,患肺癌的人更容易吸烟呢?尽管大多数研究者认为是吸烟导致了肺癌,但另一种可能性也不能完全被排除。
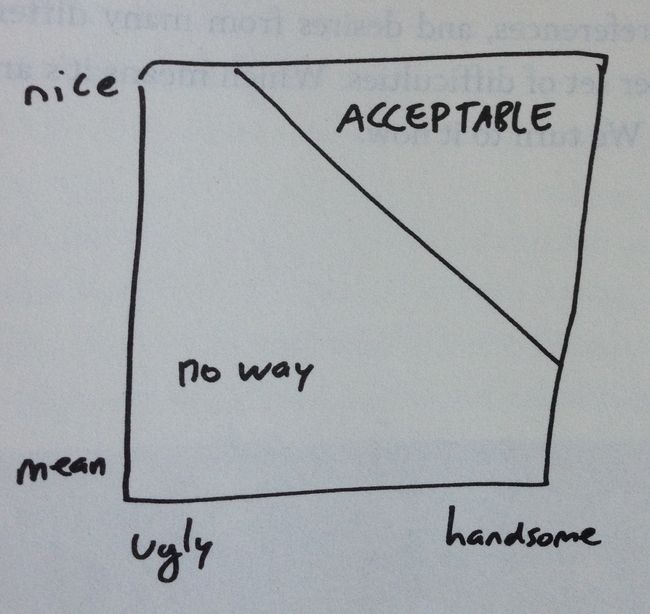
另一个值得注意的现象叫 Berkson's fallacy。当你在和人约会时,往往会发现,越帅的对象脾气越不好,而脾气好的对象往往没那么帅,为什么会这样呢?其实这是因为你已经预先剔除了一大部分人,在你可接受的约会对象里,脾气好但没那么帅以及脾气不好但帅的人所占的比例天然就比脾气又好又长得帅的人多。如果你放低标准,则会发现这一现象没那么明显了。
Part 5. Existence
17. There is no such thing as public opinion
现存的民意调查不能很好地代表实际情况,即使每个人都是理智的,但把大家的意见放到一起时,就会产生矛盾的结果。
18. "Out of nothing I have created a strange new universe"
永远有一些人走在你前面,永远有比你更聪明更富有更幸运的人,但是,不能因为这样,你就放弃自己的目标。一个学科的发展、一个社会的进步,靠的不是那些天才,而是所有人共同的努力和成果。尽管有些人在某些时候更加耀眼,但这不能抹杀其他人的存在。就好像踢足球一样,总有一些球星比其他人更优秀,但他的成功离不开整个团队的配合。
How to be right
想要得到正确的答案,一个建议是,白天拼命证明它,晚上拼命反驳它。这不仅适用于数学,而适用于所有的信仰、社交、政治、科学和哲学。