对于大量的输入数据,链表的线性访问时间太慢,不宜使用。 本章讨论一种简单的数据结构,其大部分操作的运行时间平均为O(logN)。 我们还要简述对这种数据结构在概念上的简单的修改,它保证了在最坏情形下上述的时间界。 此外,还讨论了第二种修改,对于长的指令序列它基本上给出每种操作的O(logN)运行时间。
这种数据结构叫作二叉查找树(binarysearch tree)。二叉查找树是两种库集合类TreeSet 和TreeMap实现的基础,它们用于许多应用之中。在计算机科学中树(tree)是非常有用的抽象概念,因此,我们将讨论树在其他更一般的应用中的使用。
4.1 预备知识
树(tree)可以用几种方式定义。定义树的一种自然的方式是递归的方式。一棵树是一些节点的集合。这个集合可以是空集;若不是空集,则树由称作根(root)的节点r以及0个或多个非 空的(子)树T1'Tz,…,兀组成,这些子树中每一棵的根都被来自根r的一条有向的边(edge)所连结。
每一棵子树的根叫作根r的儿子(child), 而r是每一棵子树的根的父亲(parent)。图4-1显示用递归定义的典型的树。
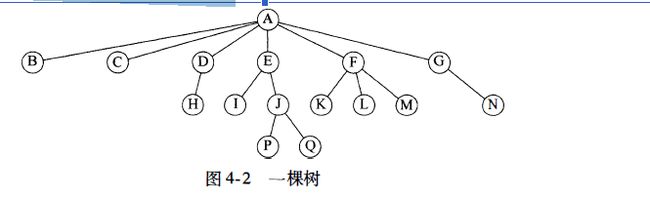
从递归定义中我们发现,一棵树是N个节点和N-1条边的集合,其中的一个节点叫作根。存在N-1条边的结论是由下面的事实得出的:每条边都将某个节点连接到它的父亲,而除去根节点外每一个节点都有一个父亲(见图4-2)。
在图4-2的树中,节点A是根。节点F有一个父亲A并且有儿子K、L和M。每一个节点可以有任意多个儿子,也可能是零个儿子。没有儿子的节点称为树叶(leaf); 上图中的树叶是B、C、H、I,p、Q、K、L,M和N。具有相同父亲的节点为兄弟(siblings); 因此,K、L和M都是兄弟。用类似的方法可以定义祖父(grandparent)和孙子(grandchild)关系。
从节点n1 到m的路径(path) 定义为节点n 1 , n2 , …,nk 的一个序列,使得对于1<= i < k节点ni是ni+ 1的父亲。这条路径的长(length) 是为该路径上的边的条数,即k -1。从每一个节点到它自己有一条长为0 的路径。注意,在一棵树中从根到每个节点恰好存在一条路径。
对任意节点ni, n,i的深度(depth) 为从根到n; 的唯一的路径的长。因此,根的深度为0。ni的高(height) 是从ni到一片树叶的最长路径的长。因此所有的树叶的高都是0。一棵树的高等于它的根的高。对于图4-2中的树,E的深度为1而高为2;F的深度为1而高也是1; 该树的高为3。一棵树的深度等于它的最深的树叶的深度;该深度总是等于这棵树的高。
如果存在从n 1 到nz 的一条路径,那么n 1 是n z 的一位祖先(ancestor) 而nz 是n1 的一个后裔(descendant) 。如果n 1!=n2 , 那么n 1 是n2 的真祖先(proper ancestor) 而n 2 是n 1 的真后裔(properdescendant) 。
4. 1. 1 树的实现
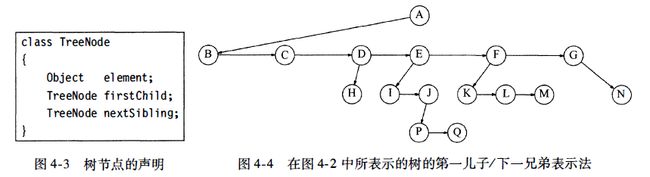
实现树的一种方法可以是在每一个节点除数据外还要有一些链,使得该节点的每一个儿子都有一个链指向它。然而,由于每个节点的儿子数可以变化很大并且事先不知道,因此在数据结构中建立到各(儿)子节点直接的链接是不可行的,因为这样会产生太多浪费的空间。实际上解决方法很简单:将每个节点的所有儿子都放在树节点的链表中。图4-3 中的声明就是典型的声明。
图4-4指出一棵树如何用这种实现方法表示出来。图中向下的箭头是指向firstChild(第一儿子)的链,而水平箭头是指向nextSibling(下一兄弟)的链。因为null 链太多了,所以没有把它们画出。
在图4-4的树中,节点E有一个链指向兄弟(F)'另一链指向儿子(/)'而有的节点这两种链都没有。
4.2 二叉树
二叉树(binary tree) 是一棵树,其中每个节点都不能有多于两个的儿子。
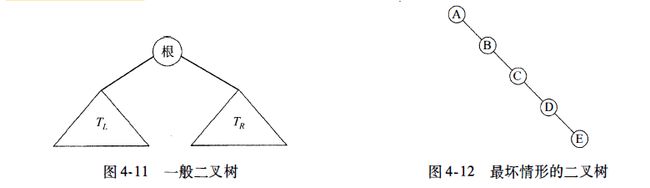
图4-11显示一棵由一个根和两棵子树组成的二叉树,子树兀和兀均可能为空。
二叉树的一个性质是一棵平均二叉树的深度要比节点个数N 小得多,这个性质有时很重要。分析表明,其平均深度为O(√n),而对于特殊类型的二叉树,即二叉查找树(binary search tree),其深度的平均值是O(log N)。
不幸的是,正如图4-12中的例子所示,这个深度是可以大到N-1的。
4.3 查找树ADT——二叉查找树
二叉树的一个重要的应用是它们在查找中的使用。假设树中的每个节点存储一项数据。 在我们的例子中,虽然任意复杂的项在 Java 中都容易处理,但为简单起见还是假设它们是整数。还将假设所有的项都是互异的,以后再处理有重复元的情况。
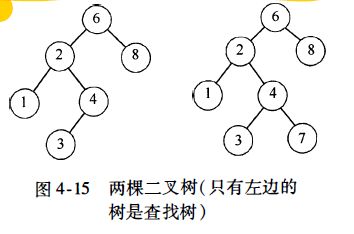
使二叉树成为二叉查找树的性质是,对于树中的每个节点X, 它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项。注意,这意味着该树所有的元素可以用某种一致的方式排序。在图4-15 中,左边的树是二叉查找树,但右边的树则不是。右边的树在其项是6的节点(该节点正好是根节点)的左子树中,有一个节点的项是7。
现在给出通常对二叉查找树进行的操作的简要描述。注意,由于树的递归定义,通常是递归地编写这些操作的例程。因为二叉查找树的平均深度是O(log N),所以一般不必担心栈空间被用尽。图4-15 两棵二叉树(只有左边的树是查找树)
二叉查找树要求所有的项都能够排序。要写出一个一般的类, 我们需要提供一个interface(接口)来表示这个性质。这个接口就是Comparable, 第1 章曾经描述过。该接口告诉我们,树中的两项总可以使用compareTo 方法进行比较。由此,我们能够确定所有其他可能的关系。特别是我们不使用equals 方法,而是根据两项相等当且仅当compareTo 方法返回O来判断相等。另一种方法是使用一个函数对象,将在4. 3. 1 节中描述。图4-16 还指出,BinaryNode 类象链表类中的节点类一样,是一个嵌套类。
https://gitee.com/sunyunjie/DataStrycturesAndAlgorithmAnalysis
4. 4 AVL树
AVL( Adelson-V elskii 和Lnadis)树是带有平衡条件(balance condition)的二叉查找树。
一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。在图4-29中,左边的树是AVL树,但是右边的树不是。每一个节点(在其节点结构中)保留高度信息。可以证明,粗略地说,一个AVL树的高度最多为1.44 log (N + 2) -1. 3 28 ,但是实际上的高度只略大于log N 。作为例子,图4-30显示了一棵具有最少节点(143)高度为9的AVL树。这棵树的左子树是高度为7且大小最小的AVL树,右子树是高度为8且大小最小的AVL树。它告诉我们,在高度为h 的AVL树中,最少节点数S(h) 由S(h)=S(h -1) +S(h -2) + 1给 出。对于h=O, S(h)= l; h=l, S(h)= 2 。函数S(h)与斐波那契数密切相关,由此推出上面提到的关于AVL树的高度的界。
因此,除去可能的插入外(我们将假设懒惰删除),所有的树操作都可以以时间O(log N)执行。当进行插入操作时,我们需要更新通向根节点路径上那些节点的所有平衡信息,而插入操作隐含着困难的原因在于,插入一个节点可能破坏AVL树的特性(例如,将6插入到图4-29中的AVL树中将会破坏关键字为8的节点处的平衡条件)。如果发生这种情况,那么就要在考虑这一步插人完成之前恢复平衡的性质。事实上,这总可以通过对树进行简单的修正来做到,我们称其为旋转(rotation)。
在插入以后,只有那些从插入点到根节点的路径上的节点的平衡可能被改变,因为只有这些节点的子树可能发生变化。当我们沿着这条路径上行到根并更新平衡信息时,可以发现一个节点,它的新平衡破坏了AVL条件。我们将指出如何在第一个这样的节点(即最深的节点)重新平衡这棵树,并证明这一重新平衡保证整个树满足AVL性质。
我们把必须重新平衡的节点叫作a。由于任意节点最多有两个儿子,因此出现高度不平衡就需要a 点的两棵子树的高度差2 。容易看出,这种不平衡可能出现在下面四种情况中:
1. 对a的左儿子的左子树进行一次插入。
2. 对a的左儿子的右子树进行一次插入。
3. 对a的右儿子的左子树进行一次插入。
4. 对a的右儿子的右子树进行一次插入。
笫一种情况是插入发生在“ 外边” 的情况(即左-左的情况或右- 右的情况),该情况通过对树的一次单旋转(single rotation) 而完成调整。第二种情况是插入发生在“ 内部” 的情形(即左- 右的情况或右- 左的情况),该情况通过稍微复杂些的双旋转(double rotation)来处理。我们将会看到,这些都是对树的基本操作,它们多次用在一些平衡树算法中。
4.5 伸展树
现在我们描述一种相对简单的数据结构,叫作伸展树(splay tree) , 它保证从空树开始连续M次对树的操作最多花费O(M log N)时间。虽然这种保证并不排除任意单次操作花费O(N)时间的可能,而且这样的界也不如每次操作最坏情形的界为O(log N)时那么强,但是实际效果却是一样的:不存在坏的输入序列。一般说来, 当M次操作的序列总的最坏情形运行时间为O(Mf(N))时,我们就说它的摊还(amortized)运行时间为0(/(N))。因此,一棵伸展树每次操作的摊还代价是O(log N)。经过一系列的操作,有的操作可能花费时间多一些,有的可能要少一些。
伸展树基于这样的事实:对于二叉查找树来说,每次操作最坏情形时间O(N) 并不坏, 只要它相对不常发生就行。任何一次访问,即使花费O(N), 仍然可能非常快。三叉查找树的间颖在于,虽然一系列访问整体都是坏的操作有可能发生,但是很罕见。此时,累积的运行时间很重要。具有最坏情形运行时间O(N)但保证对任意M次连续操作最多花费O(Mlog N)运行时间的查找树数据结构确实可以令人满意了,因为不存在坏的操作序列。
如果任意特定操作可以有最坏时间界O(N), 而我们仍然要求一个O(log N)的摊还时间界,那么很清楚,只要一个节点被访问,它就必须被移动。否则,一旦发现一个深层的节点,我们就有可能不断对它进行访问。如果这个节点不改变位置,而每次访问又花费O(N), 那么M次访问将花费O(M·N)的时间。
伸展树的基本想法是,当一个节点被访问后,它就要经过一系列AVL树的旋转被推到根上。注意,如果一个节点很深,那么在其路径上就存在许多也相对较深的节点,通过重新构造可以减少对所有这些节点的进一步访问所花费的时间。因此,如果节点过深,那么我们要求重 新构造应具有平衡这棵树(到某种程度)的作用。除在理论上给出好的时间界外,这种方法还可能有实际的效用,因为在许多应用中当一个节点被访问时,它很可能不久再被访问。研究表明,这种情况的发生比人们预想的要频繁得多。另外,伸展树还不要求保留高度或平衡信息,因此 它在某种程度上节省空间并简化代码(特别是当实现例程经过审慎考虑而被写出的时候)。
4.6 再探树的遍历
由于二叉查找树中对信息进行的排序,因而按照排序的顺序列出所有的项很简单,图4-57中的递归方法进行的就是这项工作。
一个中序遍历的一般方法是首先处理左子树,然后是当前的节点,最后处理右子树。这个算法的有趣部分除它简单的特性外,还在于其总的运行时间是O(N)。这是因为在树的每一个节点处进行的工作是常数时间的。每一个节点访问一次,而在每一个节点进行的工作是检测是否null、建立两个方法调用、并执行prin已n。由于在每个节点的工作花费常数时间以及总共有N个节点,因此运行时间为O(N)。
有时我们需要先处理两棵子树然后才能处理当前节点。例如,为了计算一个节点的高度,首先需要知道它的子树的高度。图4-58中的程序就是计算高度的。由于检查一些特殊的情况总是有益的—一当涉及递归时尤其重要,因此要注意这个例程声明树叶的高度为零,这是正确的。这种一般的遍历顺序叫作后序遍历,我们在前面也见到过。因为在每个节点的工作花费常数时间,所以总的运行时间也是O(N)
我们见过的第三种常用的遍历格式为先序遍历(preorder traversal) 。这里,当前节点在其儿子节点之前处理。这种遍历是有用的。比如,如果要想用其深度标记每一个节点,那么这种遍历就会用到。
所有这些例程有一个共同的想法,即首先处理null的情形,然后才是其余的工作。注意,此处缺少一些附加的变量。这些例程仅仅传递对作为子树的根的节点的引用,并没有声明或是传递任何附加的变最。程序越紧凑,一些愚蠢的错误出现的可能就越少。第四种遍历用得很少,叫作层序遍历(level order traversal) , 我们以前尚未见到过。在层序遍历中,所有深度为d的节点要在深度d + 1 的节点之前进行处理。层序遍历与其他类型的遍历不同的地方在于它不是递归地执行的;它用到队列,而不使用递归所默示的栈。
4.7 B树
迄今为止,我们始终假设可以把整个数据结构存储到计算机的主存中。可是,如果数据更多装不下主存,那么这就意味着必须把数据结构放到磁盘上。此时,因为大 O 模型不再适用,所以导致游戏规则发生了变化。
问题在于,大0分析假设所有的操作耗时都是相等的。然而,现在这种假设就不合适了,特别是涉及磁盘I/0的时候。例如,一台500 - MIPS的机器可能每秒执行5亿条指令。这是相当快的,主要是因为速度主要依赖于电的特性。另 方面,磁盘操作是机械运动,它的速度主 要依赖于转动磁盘和移动磁头的时间。许多磁盘以7200RPM旋转。即1 分钟转7200转;因此,1转占用1/120秒,或即8.3毫秒。平均可以认为磁盘转到一半的时候发现我们要寻找的信息,但这又被移动磁盘磁头的时间抵消,因此我们得到访问时间为8.3毫秒(这是非常宽松的估计;9 -11毫秒的访问时间更为普通)。因此,每秒大约可以进行120 次磁盘访问。若不和处理器的 速度比较,那么这听起来还是相当不错的。可是考虑到处理器的速度,5亿条指令却花费相当 于120次磁盘访问的时间。换旬话说,一次磁盘访问的价值大约是40万条指令。当然,这里每一个数据都是粗略的计算,不过相对速度还是相当清楚的:磁盘访问的代价太高了。不仅如此,处理器的速度还在以比磁盘速度快得多的速度增长(增长相当快的是磁盘容量的大小)。因此,为了节省一次磁盘访问,我们愿意进行大最的计算。几乎在所有的情况下,控制运行时间的都是磁盘访问的次数。于是,如果把磁盘访间次数减少一半,那么运行时间也将减半。
在磁盘上,典型的查找树执行如下:设想要访问佛罗里达州公民的驾驶记录。假设有1千万项,每一个关键字是32字节(代表一个名字),而 一个记录是256个字节。假设这些数据不能都装入主存,而我们 是正在使用系统的20个用户中的一个(因此有1/20 的资源)。这样,在1秒内,我们 可以执行2 500万次指令,或者执行 6次磁盘访问。
不平衡的二叉查找树是一个灾难。在最坏情形下它具有线性的深度,从而 可能需要l千万次磁盘访问。 平均来看,一次成功的查找可能需要1.38 log N次磁盘访问,由于log 10 000 000 = 24 , 因此平均一次查找需要32 次磁盘访问,或5秒的时间。在一棵典型的随机构造的树中,我们预料会有一些节点的深度要深3倍;它们需要大约100 次磁盘访问,或16秒的时间。AVL树多少要好一些。1. 44 log N 的最坏悄形不可能发生,典型的清形 是非常接近于log N。这样,一棵 AVL树平均将使用大约25次磁盘访问,需要的时间是4秒。
我们 想要把磁盘访问次数减小到一个非常小的常数,比如3 或4; 而且我们愿意写一个复杂的程序来做这件事,因为在合理情况下机器指令基本上是不占时间的。由于典型的AVL树接近 到最优的高度,因此应该清楚的是, 二叉查找树是不可行的。使用二叉查找树我们不能行进到低于log N。解法直觉上看是简单的:如果有更多的分支, 那么就有更少的高度。这样,31个节 点的理想二叉树(perlect binary tree)有5层,而31个节点的5叉树则只有3层,如图4-59所示。一棵M叉查找树(M-ary search tree)可以有M路分支。随着分支增加, 树的深度在减少。 一棵 完全二叉树(complete binary tree)的高度大约为log2 N, 而 一棵完全M叉树(complete M -ary tree) 的高度大约是logMN。
我们可以以与建立二叉查找树大致相同的方式建立M叉查找树。在二叉查找树中,需要一 个关键字来决定两个分支到底取用哪个分支;而在M叉查找树中需要Ml个关键字来决定选取哪个分支。为使这种方案在最坏的情形下有效,需要保证M叉查找树以某种方式得到平衡。否则,像二叉查找树,它可能退化成一个链表。实际上,我们甚至想要更加限制性的平衡条件,即 不想要M叉查找树退化到甚至是二叉查找树,因为那时我们又将无法摆脱logN次访问了。
实现这种想法的一种方法是使用B树。这里描述基本的B树气许多的变种和改进都是可 能的,但实现起来多少要复杂些,因为有相当多的情形需要考虑。不过,容易看到,原则上B树保证只有少数的磁盘访问。
阶为M的B树是一棵具有下列特性的树:
1. 数据项存储在树叶上。
2. 非叶节点存储直到M-1 个关键字以指示搜索的方向; 关键字L代表子树i + 1中的最小的关键字。
3. 树的根或者是一片树叶,或者其儿子数在2和M 之间。
4. 除根外,肵有非树叶节点的儿子数在「M/2]和M之间。
5. 所有的树叶都在相同的深度上并有「L/ 2 ]和L之间个数据项