精度问题
计算机精度实在不敢恭维,等于号几乎没有用,所以要引入一个极小量eps(1e-8什么的)
\(a==b \qquad \to \qquad fabs(a-b)
\(a>b \qquad \to \qquad a-b>eps\)
\(a
基础概念
1.点
不知道点是什么的可以走了
一般用坐标表示
struct Point
{
double x,y;
};2.向量
没学过向量的可以翻翻高中数学或自行百度,不想说了
我们也把向量用坐标(x,y)表示
所以一般和点共用一个结构体
如果有强迫症可以
typedef Point Vector;模长:就是向量的长度,记为\(|A|\)
double length(const Vector& v)
{
return sqrt(v.x*v.x+v.y*v.y);
}计算机算解析式极其繁琐,所以计算几何中几乎所有操作都是用向量实现的
3.直线与线段
一般用两个点或一个点和一个向量表示
其实差不多
向量运算
强烈建议大家学一下重载运算符,不会也没关系
点-点=向量
就是\(B-A=\overrightarrow {AB}\)
Vector operator -(const Point& a,const Point& b)
{
return (Vector){a.x-b.x,a.y-b.y};
}点和向量加减
Point operator +(const Point& p,const Vector& v)
{
return (Point){p.x+v.x,p.y+v.y};
}减法同理
向量乘常数
把向量伸长或缩短,或者反向
不要写成int了
Vector operator *(const Vector& a,const double& k)
{
return (Vector){a.x*k,a.y*k};
}向量加减
和向量加减点同理
点积(很重要)
定义:\(A·B=|A||B|cos\)
是个标量(没有方向)
坐标:\(A·B=x_{A} y_{A}+x_{B} y_{B}\)
double operator ^(const Vector& a,const Vector& b)//用^代替,因为叉积用的多
{
return a.x*b.x+a.y*b.y;
}几何意义:A在B所在方向的投影的模长和B的模长的乘积
可以判两个向量是否垂直
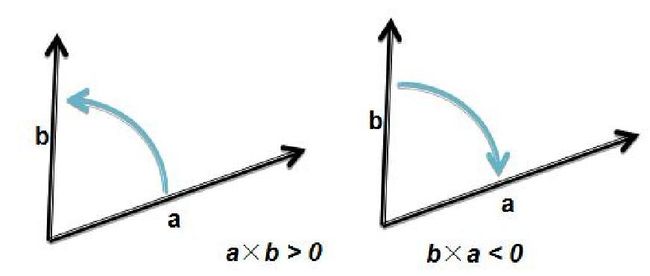
叉积(更重要)
定义:\(A \times B=|A||B|sin\)
本来是向量,但它垂直于平面,你当标量好了
坐标:\(A·B=x_{A} y_{B}-x_{B} y_{A}\)
double operator *(const Vector& a,const Vector& b)
{
return a.x*b.y-a.y*b.x;
}几何意义:A转到B所夹平行四边形的有向面积
有向指
这个用途多的多,可以判断A和B哪个在前,A、B是否共线等。
基础问题
点P是否在线段AB上
\(|PA|+|PB|=|AB|\)
点P是否在直线AB上
\(\overrightarrow {PA} \times \overrightarrow {PB} =0\)
ABC拐向
\(\overrightarrow {AB} \times \overrightarrow {AC} >0\):逆时针拐弯
凸多边形面积
\(S=\frac{1}{2} \sum _{i=1}^{n} P_{i} \times P_{i+1}\)
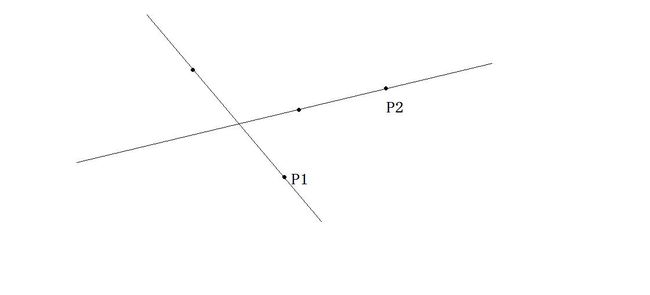
求直线交点
列方程太麻烦,考虑将向量发扬光大
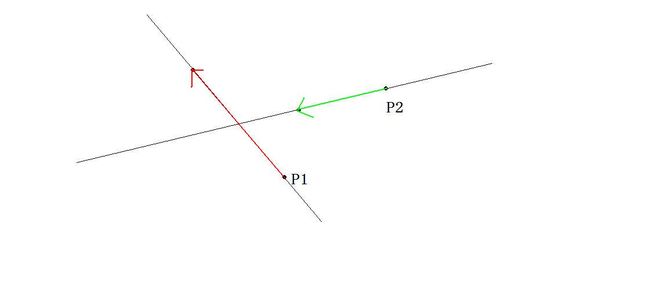
画出向量
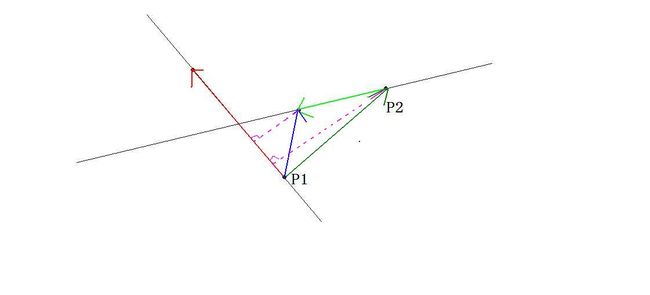
考虑算高
由叉积的几何意义,两条粉色虚线之比为(RE蓝×WA红:AC绿×WA红)
由相似,等于(无色英雄:P2到交点)
即把原谅绿延长再加上P2
算法
凸包
定义:最小的凸多边形覆盖所有点
Granham扫描法
①选出x坐标最小的点,如果相同选y坐标最小(一定在凸包上),将这个点压入栈
②所有点按极角(和最开始的点的连线与x轴的夹角)排序
③跑一遍,一直弹栈直到(s[top-1],s[top],当前点)向左拐
复杂度O(nlogn)
容易被卡精度
不知道叫什么的改进
按x第一关键字,y第二关键字排,跑完后再倒着跑一遍
精度相对较高
模板题
#include
#include
#include
#include
#define eps 1e-8
using namespace std;
struct Point
{
double x,y;
}p[10005];
typedef Point Vector;
bool operator < (const Point& a,const Point& b)
{
return a.x==b.x? a.y1&&(p[st[m]]-p[st[m-1]])*(p[i]-p[st[m-1]])<=0) m--;
st[++m]=i;
}
int k=m;
for (int i=n-1;i>=1;i--)
{
while (m>k&&(p[st[m]]-p[st[m-1]])*(p[i]-p[st[m-1]])<=0) m--;
st[++m]=i;
}
for (int i=1;i 旋转卡壳
关于此算法读音:一共24种
英文叫Rotating calipers,直译“旋转的游标卡尺”(蛤?)
也就是说卡壳指的是游标卡尺。所以卡壳是个名词,那应该读qiǎ ké
这个算法主要用于算一堆点的最长距离
其实也没名字说的那么奥妙
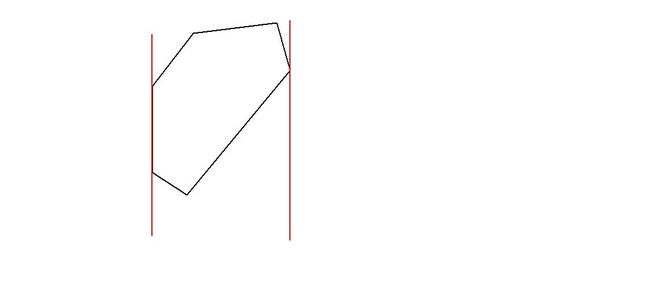
①求出凸包,特判只有2个点的情况
②假想有一组平行直线把凸包夹着
通过算面积可以找出离左边直线也许最远的点,当它比下一个点长时,就停止,用左边两个点到右边的距离更新答案。
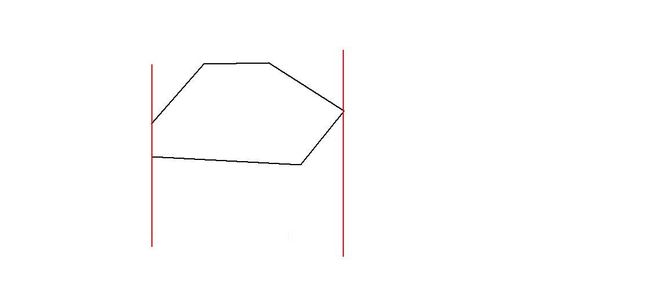
③把直线转一下,和下一条边重合,在原来的基础上把点往后挪,同样找个貌似是最远的点
(mspaint不能自定义旋转,两个可能长得不一样,望理解)
我也不知道为什么反正就是对的
直线最多转一圈,所以是O(n)的
模板
#include
#include
#include
#include
#include
#include
#include
#define MAXN 50005
#define nxt(x) ((x)%top+1)
using namespace std;
inline int read()
{
int ans=0,f=1;
char c=getchar();
while (!isdigit(c))
{
if (c=='-') f=-1;
c=getchar();
}
while (isdigit(c))
ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
return f*ans;
}
struct Point
{
int x,y;
}p[MAXN];
int s[MAXN];
int top=1;
typedef Point Vector;
bool operator <(const Point& a,const Point& b)
{
return a.x==b.x? a.y1&&(p[s[top]]-p[s[top-1]])*(p[i]-p[s[top-1]])<=0)
top--;
s[++top]=i;
}
int k=top;
for (int i=n-1;i>=1;i--)
{
while (top>k&&(p[s[top]]-p[s[top-1]])*(p[i]-p[s[top-1]])<=0)
top--;
s[++top]=i;
}
}
int getmax()
{
int ans=0;
if (top==2)
return dis(p[s[2]]-p[s[1]]);
s[top+1]=s[1];
for (int i=1,j=3;i<=top;i++)
{
while (nxt(j)!=i&&area(p[s[i]],p[s[i+1]],p[s[j]])<=area(p[s[i]],p[s[i+1]],p[s[j+1]]))
j=nxt(j);
ans=max(ans,max(dis(p[s[j]]-p[s[i]]),dis(p[s[j]]-p[s[i+1]])));
}
return ans;
}
int main()
{
n=read();
for (int i=1;i<=n;i++)
p[i].x=read(),p[i].y=read();
gethull();
printf("%d",getmax());
return 0;
}
半平面交
问题:给定一些半平面,求它们的交
细节问题:
1.半平面指在给出的直线一边的平面,具体哪一边看题。由凸多边形定义,它一定是凸多边形
2.交可以是多边形,还可以是直线、射线、线段、点、空集,也可以不封闭。具体看题。
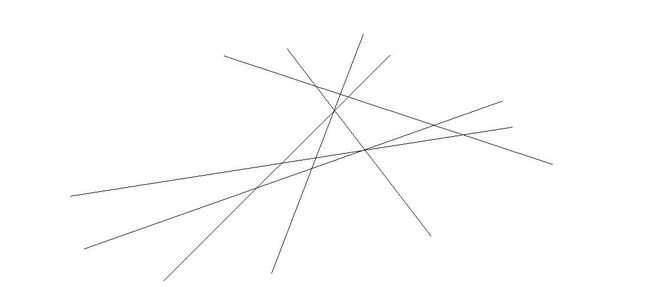
为了方便理解,先放一道题
算法流程:
①所有直线按和x轴夹角排序;如果有相同的,只保留最优的(上面的题是更靠“内”的,写写就知道了)
②维护一个双端队列(因为坐标轴上转了一圈会回来)
跑一遍所有直线
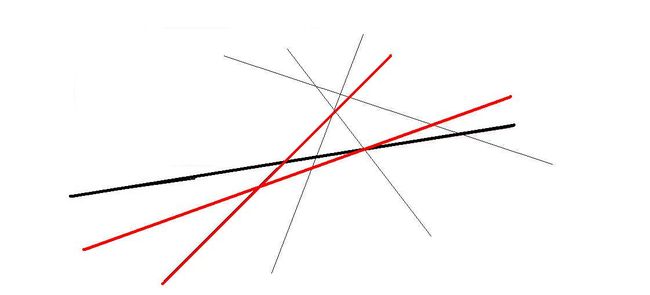
while(当前直线在队首两直线交点外)//“外”是指加入这条直线后前两个半平面的交会变化
弹队首;
while(当前直线在队尾两直线交点外)
弹队尾;
③清除多余直线
while(队尾直线在队首两直线交点外)
弹队首;
while(队首直线在队尾两直线交点外)
弹队尾;
#include
#include
#include
#include
#include
#define MAXN 505
#define MAXM 55
const double eps=1e-8;
using namespace std;
struct Point
{
double x,y;
}p[MAXN];
typedef Point Vector;
double operator *(const Vector& a,const Vector& b)
{
return a.x*b.y-a.y*b.x;
}
Vector operator *(const Vector& a,const double& k)
{
return (Vector){a.x*k,a.y*k};
}
Point operator +(const Point& p,const Vector& v)
{
return (Point){p.x+v.x,p.y+v.y};
}
struct Line
{
Point a,b;
double d;
}l[MAXN];
int sta[MAXN];
int top;
Vector operator -(const Point& a,const Point& b)
{
return (Vector){a.x-b.x,a.y-b.y};
}
Point inter(const Line& x,const Line& y)
{
Point p1=x.a,p2=y.a;
Vector v1=x.b-p1,v2=y.b-p2,u=p2-p1;
Point p=p2+v2*((u*v1)/(v1*v2));
return p;
}
int sign(const double& a)
{
if (fabs(a)>eps)
return a>0? 1:-1;
return 0;
}
bool operator <(const Line& a,const Line& b)
{
if (sign(a.d-b.d)==0)
return sign((a.b-a.a)*(b.b-a.a))>0;
return sign(a.d-b.d)<0;
}
int n,m;
int q[MAXN],head,tail;
bool check(const Line& x,const Line& y,const Line& z)
{
Point p=inter(x,y);
return sign((z.b-z.a)*(p-z.a))<0;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
int mi;
scanf("%d",&mi);
for (int j=1;j<=mi;j++)
scanf("%lf%lf",&p[j].x,&p[j].y);
p[mi+1]=p[1];
for (int j=1;j<=mi;j++)
{
++m;
l[m].a=p[j];
l[m].b=p[j+1];
}
}
n=m;
for (int i=1;i<=n;i++)
l[i].d=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
sort(l+1,l+n+1);
int cnt=0;
for (int i=1;i<=n;i++)
{
if (sign(l[i].d-l[i-1].d)!=0)
++cnt;
l[cnt]=l[i];
}
head=1,tail=0;
q[++tail]=1,q[++tail]=2;
for (int i=3;i<=cnt;i++)
{
while (head2)
for (int i=1;i<=n;i++)
ans+=(p[i]*p[i+1]);
ans=fabs(ans)/2.0;
printf("%.3f",ans);
return 0;
}