1 大O:数步数
数步数 为了统一描述,大O不关注算法所用的时间,只关注其所用的步数。
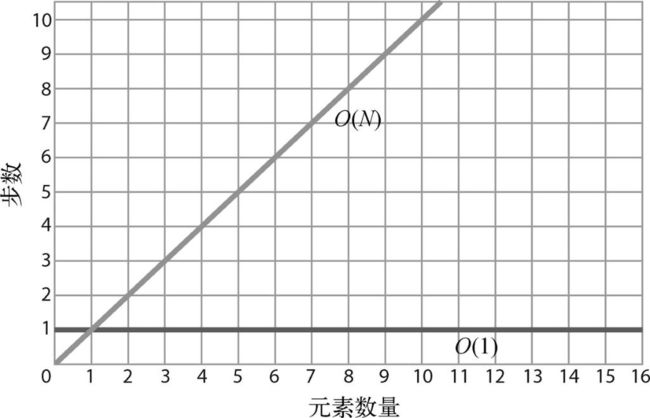
数组不论多大,读取都只需1步。用大O记法来表示,就是:O(1) 很多人将其读作“大O1”,也有些人读成“1数量级”。一般读成“O1”。虽然大O记法有很多种读法,但写法只有一种。
若用大O记法来描述一种处理一个N元素的数组需花N步的算法的效率,很简单,就是O(N)。
2 常数时间与线性时间
大O解答的是这样的问题:当数据增长时,步数如何变化?
O(N)算法所需的步数等于数据量,意思是当数组增加一个元素时,O(N)算法就要增加1步。而O(1)算法无论面对多大的数组,其步数都不变。
O(N)呈现为一条对角线。O(N)也被称为线性时间。
O(1)则为一条水平线,O(1)也被称为常数时间。
因为大O主要关注的是数据量变动时算法的性能变化,不管数据量怎样变化,算法的步数都恒定,所以这也是常数时间,也可以表示为O(1)。
O(1)就是用来表示所有数据增长但步数不变的算法。
3 同一算法,不同场景
线性查找并不总是O(N)的。当要找的元素在数组末尾,那确实是O(N)。但如果它在数组开头,1步就能找到的话,那么技术上来说应该是O(1)。所以概括来说,线性查找的最好情况是O(1),最坏情况是O(N)。大O记法一般都是指最坏情况。
4 第三种算法
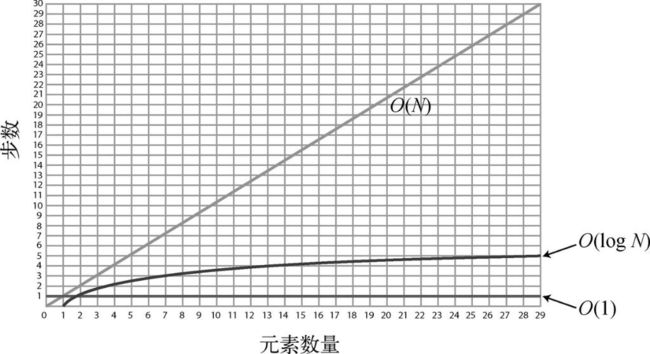
二分查找的大O记法是:O(logN)我将其读作“O log N”。归于此类的算法,它们的时间复杂度都叫作对数时间。
简单来说,O(logN)意味着该算法当数据量翻倍时,步数加1。
5 对数
log即是对数(logarithm)。
对数是指数的反函数
6 解释O(log N)
当我们说O(logN)时,其实指的是O(log2N),不过为了方便就省略了2而已。
二分查找所干的事情。它就是不断地将数组拆成两半,直至范围缩小到只剩你要找的那个元素。
简单来说,O(logN)算法的步数等于二分数据直至元素剩余1个的次数。
每次数据量翻倍时,O(N)算法的步数也跟着翻倍,O(logN)算法却只需加1。
参考:数据结构与算法图解.3