吴裕雄--天生自然神经网络与深度学习实战Python+Keras+TensorFlow：神经网络的理论基础

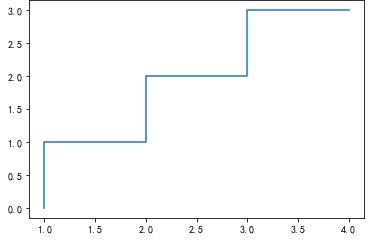
#绘制步调函数图像
import matplotlib.pyplot as plt

x = [1,2,3,4]
y = [0, 1, 2, 3]
plt.step(x, y)
plt.show()

 

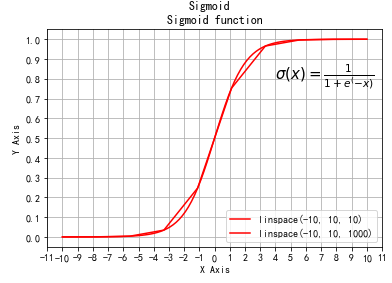
import numpy as np
import pylab as plt
from matplotlib import pylab

#设置simoid函数计算流程
def sigmoid(x):
    return (1 / (1 + np.exp(-x)))

mySamples = []
mySigmoid = []
#设置函数绘制区间
x = plt.linspace(-10, 10, 10)
y = plt.linspace(-10, 10, 100)
#在给定区间内绘制sigmoid函数值点，形成函数曲线
plt.plot(x, sigmoid(x), 'r', label = 'linspace(-10, 10, 10)')
plt.plot(y, sigmoid(y), 'r', label='linspace(-10, 10, 1000)')
plt.grid()
plt.title('Sigmoid function')
plt.suptitle('Sigmoid')
plt.legend(loc='lower right')
#给绘制曲线图像做标注
plt.text(4, 0.8, r'$\sigma(x)=\frac{1}{1+e^(-x)}$', fontsize=15)
plt.gca().xaxis.set_major_locator(plt.MultipleLocator(1))
plt.gca().yaxis.set_major_locator(plt.MultipleLocator(0.1))
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.show()

import numpy as np

W = np.array([
    [0.9, 0.3],
    [0.2, 0.8]
])
I = np.array([1.0, 0.5])
X = W.dot(I)
print(X)

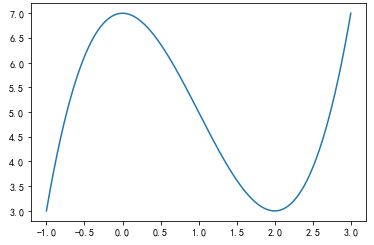
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib qt

function = lambda x: (x ** 3) - 3* (x**2) + 7  #设置要绘制的函数表达式
x = np.linspace(-1, 3, 500) #在区间[1,3]内绘制函数图像
plt.plot(x, function(x))
plt.show()

 

 

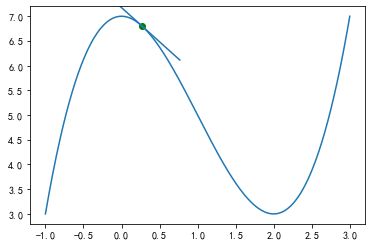
def  deriv(x):
    '''
    计算函数x^3-2x^2+7在任一点处的导函数，其导函数形式为3x^2-6x
    '''
    x_deriv = 3 * (x ** 2) - (6 * x)
    return x_deriv

def  tangent_line(x_0):
    '''
    在给定点x_0处绘制函数切线
    '''
    x = np.linspace(-1, 3, 500) 
    y = function(x)
    y_0 = function(x_0)
    y_tan = deriv(x_0) * (x - x_0) + y_0
    plt.plot(x, y, 'r-')  #绘制函数图像
    plt.plot(x, y_tan, 'b-')  #绘制给定点处的切线
    plt.show()
tangent_line(1.5) #绘制函数在点1.5处的切线

 

 

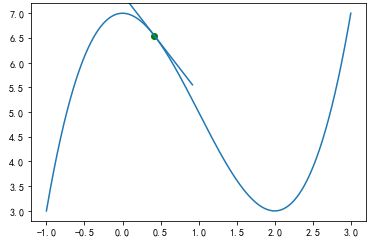
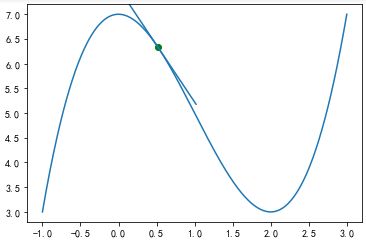
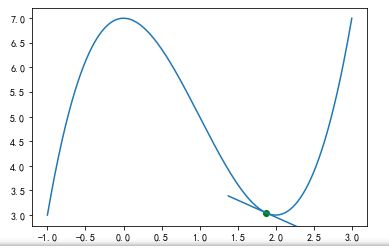
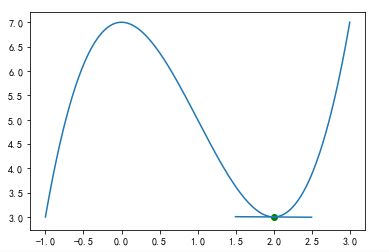
import matplotlib.lines as mlines

def  step(x_new, x_prev, precision, l_r):
    '''
    动态展现梯度下降法寻找函数最低点过程，x_new对应函数起始点，
    x_prev表示函数点调整前的值，precision表示x点调整前和调整后的差异，
    l_r表示x点每次调整幅度的大小
    '''
    x_list, y_list = [x_new], [function(x_new)]
    while abs(x_new - x_prev) > precision:
        x_prev = x_new  #记录调整前x点值
        d_x = -deriv(x_prev) #沿着切线下降的方向调整x的值
        x_new = x_prev + (l_r * d_x)  #获得调整后x的值
        x_list.append(x_new)
        y_list.append(function(x_new))
    for i in range(len(x_list)):
        plt.clf()
        x = np.linspace(-1, 3, 500) 
        y = function(x)
        plt.plot(x, function(x))  #先绘制函数曲线
        plt.scatter(x_list[i], y_list[i], c="g")
        y_i = function(x_list[i])  
        tan = deriv(x_list[i]) #当前点处切线斜率，对应切线方程为y = tan* (x-x_list[i]) + y_i
        tanline_begin = tan*(-0.5) + y_i
        tanline_end = tan*(0.5) + y_i
        ax = plt.gca()
        l = mlines.Line2D([x_list[i] - 0.5, x_list[i] + 0.5], [tanline_begin, tanline_end])
        ax.add_line(l)
        plt.pause(1)
    plt.show()
step(0.1, 0, 0.001, 0.05)