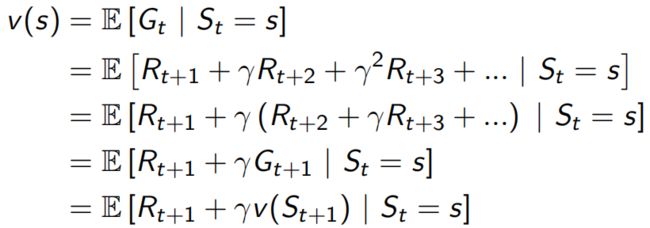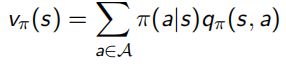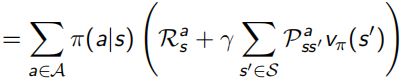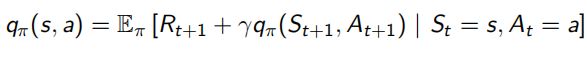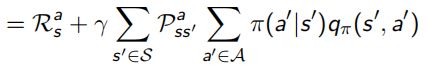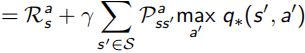本系列强化学习内容来源自对David Silver课程的学习 课程链接http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html
之前接触过RL(Reinforcement Learning) 并且在组会学习轮讲里讲过一次Policy Gradient,但是由于基础概念不清,虽然当时懂了 但随后很快就忘。。虽然现在写这个系列有些晚(没有好好跟上知识潮流o(╥﹏╥)o),但希望能够系统的重新学一遍RL,达到遇到问题能够自动想RL的解决方法的程度。。
目录
1. 基础概念
1.1 强化学习为何重要
1.2 agent和environment
1.3 agent的组成和分类
2. Markov Decision Process(MDP)
2.1 Markov Reward Process(MRP)
2.2 Markov Decision Process(MDP)
2.3 Optimal Policy求最优解
2.4 Partial Observable Markov Decision Process(POMDP)
一、 基础概念
强化学习为何重要?
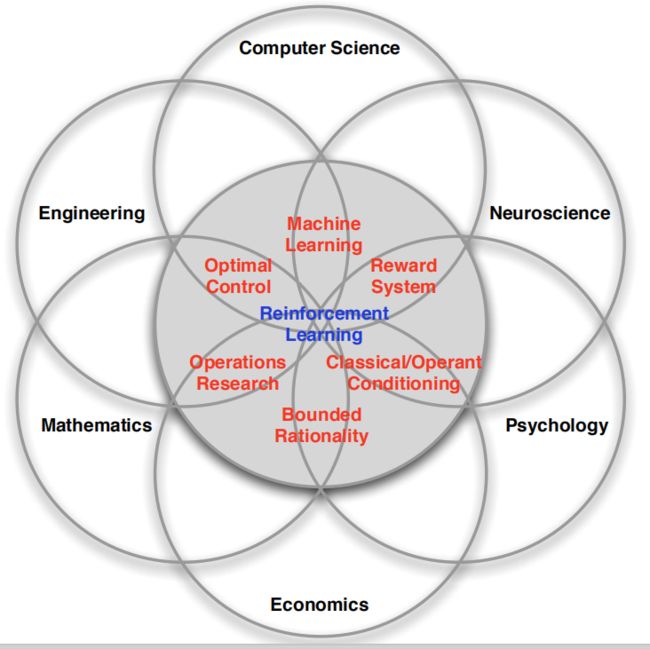
因为它的原理 在所有学科中都有应用(下图左),DeepMind与哈佛大学最新研究也证明,人脑中存在“分布强化学习”,奖励为多巴胺(表示surprise的信号)。并且,RL和监督/无监督学习一起构成机器学习(下图右),它的“supervisor”是一个会延迟反应的cumulative reward(总回报)。
强化学习过程:
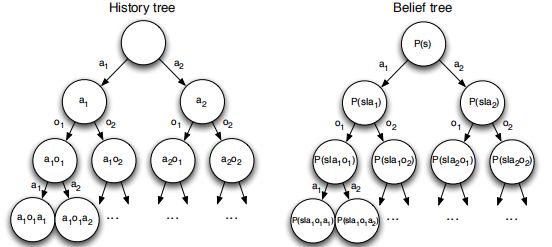
主要包含Agent和Environment两个主体,RL的过程在它们中展开(下图左):某时刻t,Agent观测环境Ot、根据自己所知的回报Rt、产生动作At,Environment接收到At后、时间前进成t+1、环境变换Ot+1、回报更新Rt+1。这个过程序列就叫history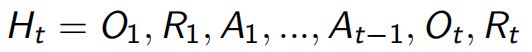 ,某个时刻状态 就叫State(分成Set和Sat)。
,某个时刻状态 就叫State(分成Set和Sat)。
Sat可以通过Ht得出(Sat=f(Ht)),并且如果P[St+1|St] = P[St+1|S1,...,St],即得到了St后可以把之前的history都丢掉 当前状态只与前一状态有关,状态St就是Markov的。
Set不一定可知,如果fully observable可知 则:Ot=Sat=Set,这是一个Markov decision process(MDP),也是课程的大部分内容;如果partial observable部分可知 则:Sat != Set, 这是一个Partial observable MDP(POMDP),此时agent必须要构建自己状态的表达,可以是来自history![]() , 可以是对环境的预测
, 可以是对环境的预测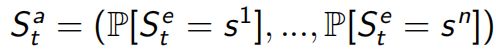 ,可以是RNN
,可以是RNN![]() 。。。
。。。
Agent的组成和分类:
Agent可能包含以下一个或者多个部件:policy,value function,model。
所以agent可以分成多类(上图右),对于policy和value function这两个来说,用policy - Policy Based,用value function - Value Based,都用 - Actor Critic。对于model来说,有model - Model Based,没有model - Model Free。
那么它们各自是什么呢?
policy和value function都可以达到决定在当前state下产生什么行为action的效果。policy(记π)是函数(包括deterministic:相同s相同a — a=π(s), 和stochastic:显示此s下出现某a的可能性 — π(a|s)=P[At = a | St = s])。 value function是每个state的未来回报预测 即![]() ,这样就能选择action使其达到更优的state。
,这样就能选择action使其达到更优的state。
而model是agent对于环境下一步做什么的预测。包含下一步状态的预测P和对于immediate reward的预测R。
这样,agent通过不断和环境的交互,提升自己做决策的能力。squential decision making过程中有两个基本问题,environment如果一开始unknown 则是RL,如果一开始known 则是planning。一个常用的强化学习问题解决思路是,先学习环境如何工作得到一个模型,然后利用这个模型进行规划。
强化学习也是一个不断试错的过程(trial-and-error learning),从而可以将这个学习过程分成exploration(探索更多environment信息)和exploitation(利用已有信息最大化reward)两部分。
也可以分成prediction和control两部分,prediction是预测按照当前policy走会有什么结果,control是更近一层,在多个policy中选取total reward最大的一个最优policy。
二、Markov Decision Process(MDP)
MDP之所以重要,是因为几乎所有RL问题都可以转换为MDP的格式
在学MDP前,最基本的是Markov Process(Chain), (见下图),每一行的概率和为1。
(见下图),每一行的概率和为1。
Markov Reward Process(MRP)
需要注意的是MRP和MDP的区别,MRP由![]() 。
。
回报函数 ,是当前状态所获得的回报的数学期望(类似于取平均值)。前面写过RL中t+1是在agent做出action后发生的,仍旧是当前状态下,即意思是不管在这个状态下做什么action,Rs=Rt+1都一定的。
,是当前状态所获得的回报的数学期望(类似于取平均值)。前面写过RL中t+1是在agent做出action后发生的,仍旧是当前状态下,即意思是不管在这个状态下做什么action,Rs=Rt+1都一定的。
γ是一个未来对现在影响的数学上的表达,γ=0,完全短视不考虑未来,γ=1,undiscount未来的所有状态都考虑。γ的加入主要是因为一是会削弱MP中环的影响,二是模型对未来的估计不一定准确。
所以总的discounted的回报Gt, ,这里是求和的是在t时刻随机采样产生的一系列状态点。
,这里是求和的是在t时刻随机采样产生的一系列状态点。
根据Gt,value function可以换一种写法 ,类似于采样所有s状态下的Gt取平均值。
,类似于采样所有s状态下的Gt取平均值。
后来Bellman看到这个value function表达又做了化简(下图),即可以将value function看做immediate回报Rt+1和下一个状态的价值discount后的和,这就是Bellman Equation贝尔曼方程,可以写成 的格式(v=R+γPv),此时是线性的可以解出
的格式(v=R+γPv),此时是线性的可以解出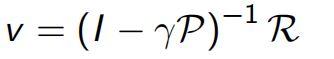 ,求解复杂度O(n3),可以用线性规划和Temporal-Difference Learning等方法解。
,求解复杂度O(n3),可以用线性规划和Temporal-Difference Learning等方法解。
举例如下图的MP过程图中,每个节点就表示当前状态s,里面数字是v(s)。比如v(s)=4.1的节点,求法是0.6*(-2+0.9*10)+0.4*(-2+0.9*1.9)=4.084,并且4.084≈4.1说明此时已经达到self-consistant状态。
Markov Decision Process(MDP)
马尔可夫决策过程相较于MRP多引入了action动作的因素,MDP的格式
并且除了之前的state-value function V(s),还加入了action-value function q(s, a)表示在状态s下采取动作a会得到什么回报:
Bellman同样对这两个value function做了化简,化简后的结果称为Bellman Expectation Equation:
Bellman Expectation Equation推导过程(上下两式子结合起来看):
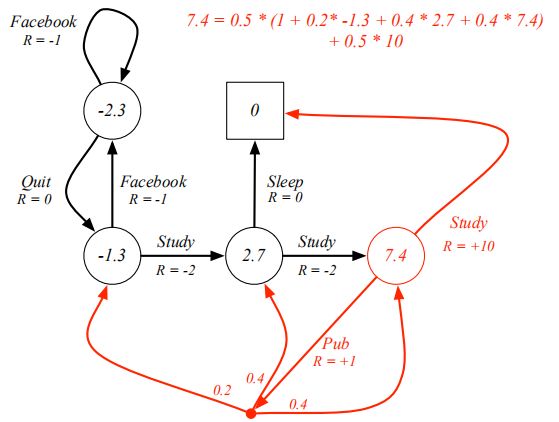
比如在下面这个例子中,7.4这个节点的v(s)更新方法如下 —— 现在已经self-consistant,每个action默认概率相同。
Optimal policy求最优解
通过这些设定,就可以进行最优策略的求解,即control,多个policy中选取最优的一个,可以看做下面的式子。
当最优的action-value function得知后,就可以知道当前状态下应该选哪个action,从而直接求出最优策略。相当于只要知道了action-value function 就什么都知道了:
这里Bellman又出现了,他化简上面对value function求解的式子,得到了一个更明了的表示叫做Bellman Optimality Equation:
意思是使用这个Bellman Optimality Equation,就可以得到state-value和action-value两个函数最优解,从而获得整个问题的最优策略,问题就能解决啦。
可惜的是,由于过程中涉及max,方程变得不可导了。因此求解的方法有value/policy iteration,Q-learning,SARSA等方法,将在之后的文章中介绍。
Partial Observable Markov Decision Process(POMDP)
部分可观测的马尔可夫决策过程,POMDP由
POMDP可以被分解成history tree和belief tree,如下图:
但是更详细的内容课程里也没有介绍,之后感兴趣的话会专门补充的。。。。
总而言之,本文主要介绍了强化学习的基本思路过程,和问题的最优解是怎么寻找的。之后会继续写出寻找问题最优解的具体技术支持。嗯。。一定要坚持写下去啊٩( 'ω' )و ! 学习使我快乐,总结使我收获\(^o^)/,黑黑