一阶导数与Soble算子
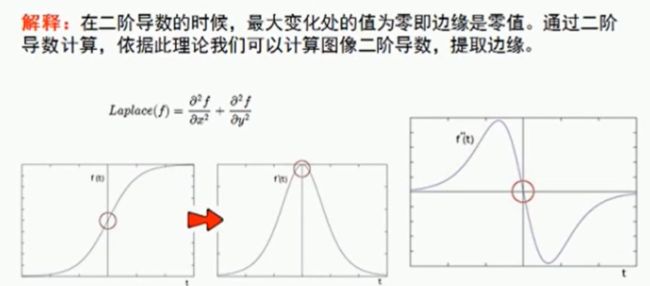
二阶导数与拉普拉斯算子
import cv2 as cv
import numpy as np
# 图像梯度(由x,y方向上的偏导数和偏移构成),有一阶导数(sobel算子)和二阶导数(Laplace算子)
# 用于求解图像边缘,一阶的极大值,二阶的零点
# 一阶偏导在图像中为一阶差分,再变成算子(即权值)与图像像素值乘积相加,二阶同理
def sobel_demo(image):
grad_x = cv.Sobel(image, cv.CV_32F, 1, 0) # 采用Scharr边缘更突出
grad_y = cv.Sobel(image, cv.CV_32F, 0, 1)
gradx = cv.convertScaleAbs(grad_x) # 由于算完的图像有正有负,所以对其取绝对值
grady = cv.convertScaleAbs(grad_y)
# 计算两个图像的权值和,dst = src1*alpha + src2*beta + gamma
gradxy = cv.addWeighted(gradx, 0.5, grady, 0.5, 0)
cv.imshow("gradx", gradx)
cv.imshow("grady", grady)
cv.imshow("gradient", gradxy)
def laplace_demo(image): # 二阶导数,边缘更细
dst = cv.Laplacian(image,cv.CV_32F)
lpls = cv.convertScaleAbs(dst)
cv.imshow("laplace_demo", lpls)
def custom_laplace(image):
# 以下算子与上面的Laplace_demo()是一样的,增强采用np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])
kernel = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]])
dst = cv.filter2D(image, cv.CV_32F, kernel=kernel)
lpls = cv.convertScaleAbs(dst)
cv.imshow("custom_laplace", lpls)
def main():
src = cv.imread("../images/lena.jpg")
cv.imshow("lena",src)
# sobel_demo(src)
laplace_demo(src)
custom_laplace(src)
cv.waitKey(0) # 等有键输入或者1000ms后自动将窗口消除,0表示只用键输入结束窗口
cv.destroyAllWindows() # 关闭所有窗口
if __name__ == '__main__':
main()