树,总共包含4节内容。具体如下:
1.树、二叉树
2.二叉查找树
3.平衡二叉树、红黑树
4.递归树
一、树
1.树的常用概念
根节点(Root)、叶子节点(Leaf)、父节点(Parent)、子节点(Child)、兄弟节点(Siblings),还有节点的高度、深度以及层数,树的高度。
Root: Top node in a tree
Child: Nodes that are next to each other and connected downwards
Parent: Converse notion of child
Siblings: Nodes with the same parent
Descendant: Node reachable by repeated proceeding from parent to child
Ancestor: Node reachable by repeated proceeding from child to parent.
Leaf: Node with no children
Internal node: Node with at least one child
External node: Node with no children
2.概念解释
节点:树中的每个元素称为节点
父子关系:相邻两节点的连线,称为父子关系
根节点:没有父节点的节点
叶子节点:没有子节点的节点
父节点:指向子节点的节点
子节点:被父节点指向的节点
兄弟节点:具有相同父节点的多个节点称为兄弟节点关系
节点的高度:节点到叶子节点的最长路径所包含的边数
节点的深度:根节点到节点的路径所包含的边数
节点的层数:节点的深度+1(根节点的层数是1)
树的高度:等于根节点的高度
二、二叉树
1.概念
①什么是二叉树?
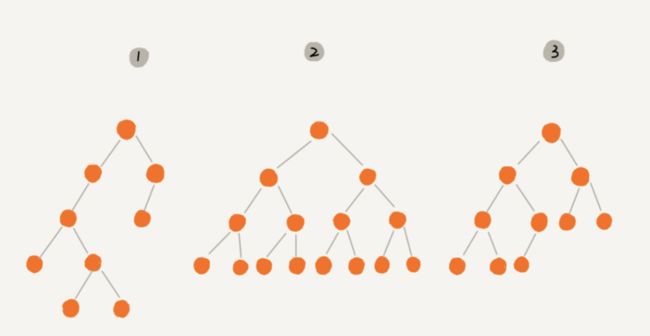
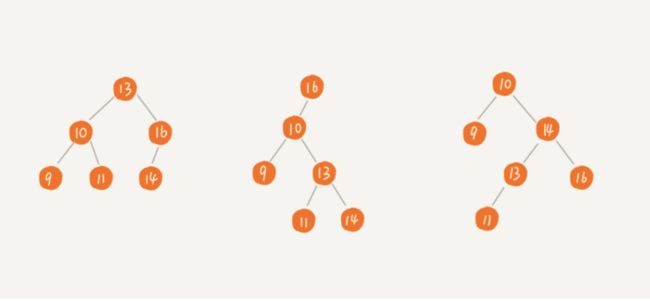
每个节点最多只有2个子节点的树,这两个节点分别是左子节点和右子节点。如下图123
②什么是满二叉树?
有一种二叉树,除了叶子节点外,每个节点都有左右两个子节点,这种二叉树叫做满二叉树。如下图2
③什么是完全二叉树?
有一种二叉树,叶子节点都在最底下两层,最后一层叶子节都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树。如下图3
2.完全二叉树的存储
①链式存储
每个节点由3个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。这种存储方式比较常用,大部分二叉树代码都是通过这种方式实现的。
C语言实现二叉树的创建
/* Includes structure for a node and a newNode() function which
can be used to create a new node in the tree.
It is assumed that the data in nodes will be an integer, though
function can be modified according to the data type, easily.
*/
#include
#include
struct node
{
struct node *leftNode;
int data;
struct node *rightNode;
};
struct node *newNode(int data)
{
struct node *node = (struct node *)malloc(sizeof(struct node));
node->leftNode = NULL;
node->data = data;
node->rightNode = NULL;
return node;
}
int main(void)
{
/* new node can be created here as :-
struct node *nameOfNode = newNode(data);
and tree can be formed by creating further nodes at
nameOfNode->leftNode and so on.
*/
return 0;
}
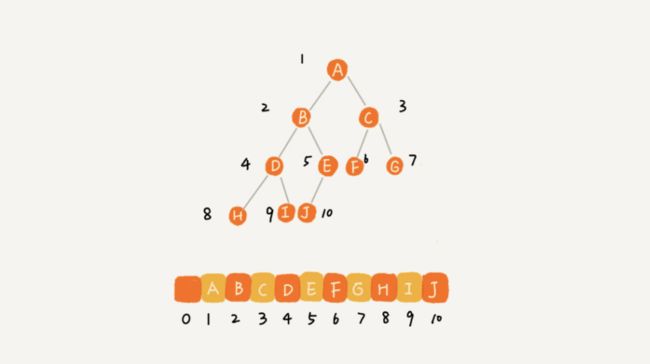
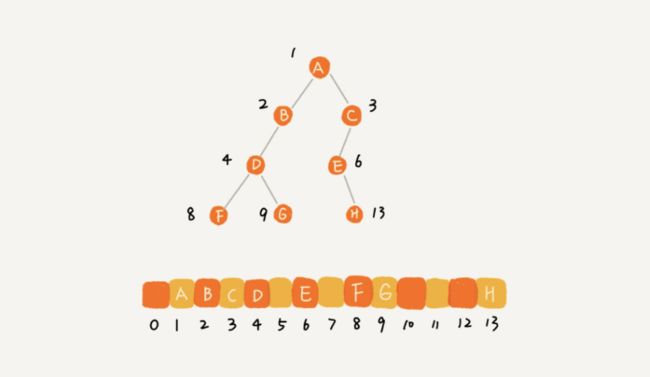
②顺序存储
用数组来存储,对于完全二叉树,如果节点X存储在数组中的下标为i,那么它的左子节点的存储下标为2i,右子节点的下标为2i+1,反过来,下标i/2位置存储的就是该节点的父节点。注意,根节点存储在下标为1的位置。完全二叉树用数组来存储时最省内存的方式。
3.二叉树的遍历
①前序遍历:对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
②中序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它的本身,最后打印它的右子树。
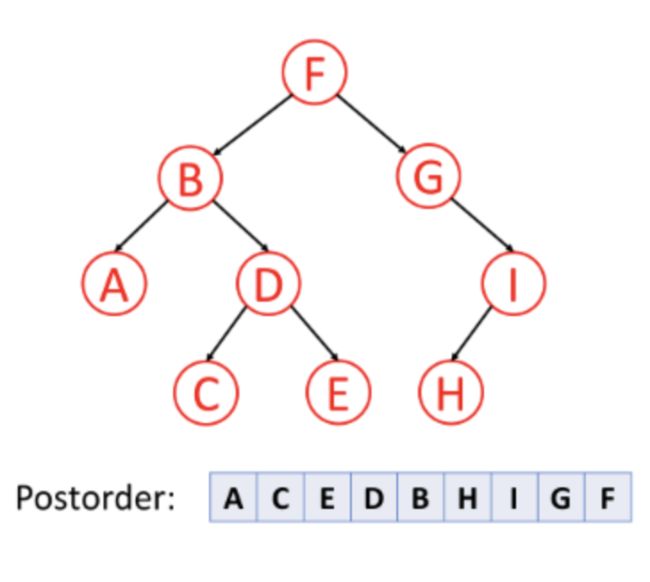
③后序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印它本身。
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
时间复杂度:3种遍历方式中,每个节点最多会被访问2次,所以时间复杂度是O(n)。
C语言二叉树三种遍历的实现
/* Includes the functions for Recursive Traversals
of a Binary Tree. It is assumed that nodes and
tree have been created as per create_node.c
*/
#include
void inOrderTraversal(struct node *node)
{
if(node == NULL) //if tree is empty
return;
inOrderTraversal(node->leftNode);
printf("\t%d\t", node->data);
inOrderTraversal(node->rightNode);
}
void preOrderTraversal(struct node *node)
{
if(node == NULL) //if tree is empty
return;
printf("\t%d\t", node->data);
preOrderTraversal(node->leftNode);
preOrderTraversal(node->rightNode);
}
void postOrderTraversal(struct node *node)
{
if(node == NULL) //if tree is empty
return;
postOrderTraversal(node->leftNode);
postOrderTraversal(node->rightNode);
printf("\t%d\t",node->data);
}
int main(void)
{
/* traversals can be done by simply invoking the
function with a pointer to the root node.
*/
return 0;
}
三种遍历的示范:
值得注意的是,当你删除树中的节点时,删除过程将按照后序遍历的顺序进行。 也就是说,当你删除一个节点时,你将首先删除它的左节点和它的右边的节点,然后再删除节点本身。
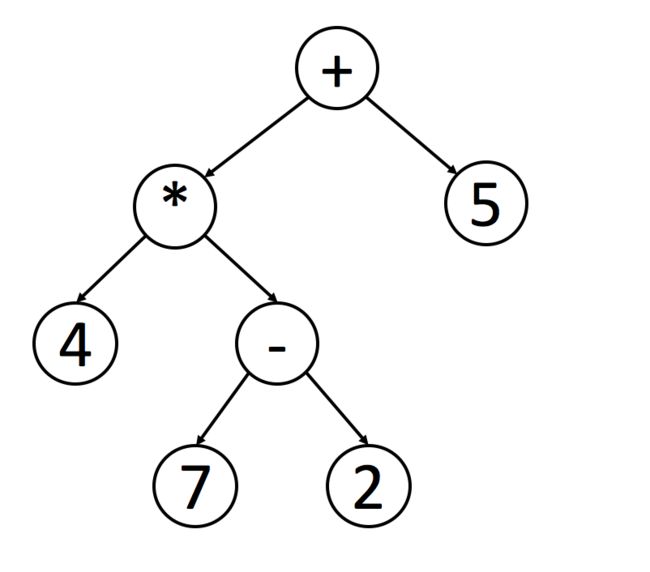
另外,后序在数学表达中被广泛使用。 编写程序来解析后缀表示法更为容易。 这里是一个例子:
您可以使用中序遍历轻松找出原始表达式。 但是程序处理这个表达式时并不容易,因为你必须检查操作的优先级。
如果你想对这棵树进行后序遍历,使用栈来处理表达式会变得更加容易。 每遇到一个操作符,就可以从栈中弹出栈顶的两个元素,计算并将结果返回到栈中。
二叉查找树(binary search tree)
1,二叉查找树最大的特点是:支持动态数据集合的快速插入,删除,查找操作
2,二叉查找树的要求:在树中的任意一个节点,其中左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
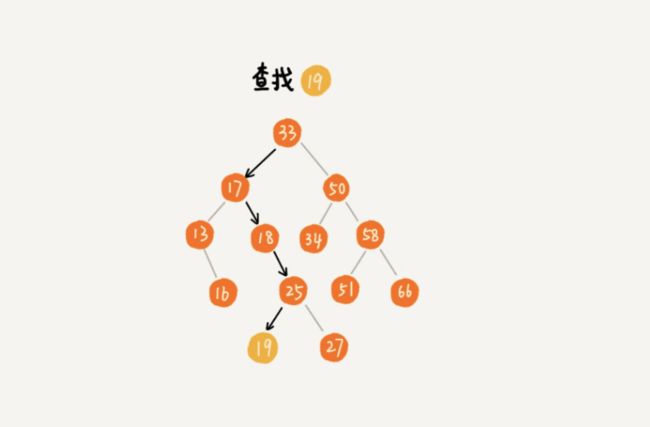
3,二叉查找树的查找操作
先取根节点,如果他等于要查找的数据,就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找
Java语言实现,查找操作
public class BinarySearchTree {
private Node tree;
public Node find(int data) {
Node p = tree;
while (p != null) {
if (data < p.data) p = p.left;
else if (data > p.data) p = p.right;
else return p;
}
return null;
}
public static class Node {
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data = data;
}
}
}
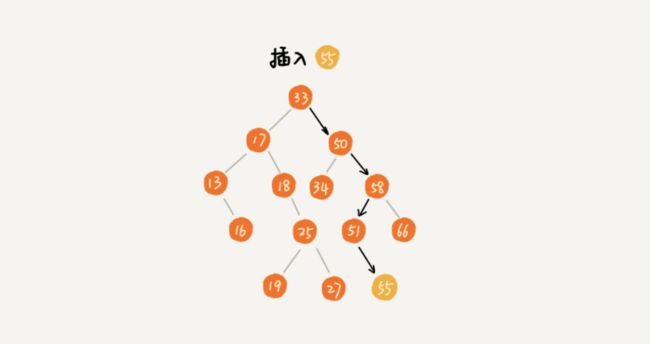
4,二叉查找树的插入操作
二叉查找树的插入过程有些类似查找操作。新插入的数据一般都是在叶子节点上,所以只需要从根节点开始,依次比较要插入的数据和节点的大小关系。
如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插入右子节点的位置;如果不为空,就在递归遍历右子树,查找插入位置。
java语言实现二叉查找树的插入操作
public void insert(int data) {
if (tree == null) {
tree = new Node(data);
return;
}
Node p = tree;
while (p != null) {
if (data > p.data) {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
} else { // data < p.data
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
5,二叉查找树的删除操作
二叉查找树的删除要分三种情况:
①:如果要删除的节点没有子节点,只需要直接将父节点中指向要删除节点的指针置为为null。
②:如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。
③:如果要删除的节点有两个子节点,我们需要找到这个节点的右子节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以就可以应用上面两条规则来删除这个最小节点。
java语言实现,二叉树的删除操作
public void delete(int data) {
Node p = tree; // p指向要删除的节点,初始化指向根节点
Node pp = null; // pp记录的是p的父节点
while (p != null && p.data != data) {
pp = p;
if (data > p.data) p = p.right;
else p = p.left;
}
if (p == null) return; // 没有找到
// 要删除的节点有两个子节点
if (p.left != null && p.right != null) { // 查找右子树中最小节点
Node minP = p.right;
Node minPP = p; // minPP表示minP的父节点
while (minP.left != null) {
minPP = minP;
minP = minP.left;
}
p.data = minP.data; // 将minP的数据替换到p中
p = minP; // 下面就变成了删除minP了
pp = minPP;
}
// 删除节点是叶子节点或者仅有一个子节点
Node child; // p的子节点
if (p.left != null) child = p.left;
else if (p.right != null) child = p.right;
else child = null;
if (pp == null) tree = child; // 删除的是根节点
else if (pp.left == p) pp.left = child;
else pp.right = child;
}
6,二叉查找树的其他操作
除了插入,删除,查找操作之外,二叉查找树中还可以可以支持快速地查找最大节点和最小节点,前驱节点和后继节点。
二叉查找树还有一个重要的特性:中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是O(n),非常高效。因此,二叉查找树也叫二叉排序树。
7,二叉查找树支持重复数据
在实际开发中,是在二叉查找树中存储的对象,我们利用对象的某个字段作为键值(key)来构建二叉查找树,并把对象中的其他字段叫作卫星数据。
针对:如果存储两个对象键值相同的处理方式:
第一种方式:二叉查找树中每个节点不仅会存储一个数据,因此可通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
第二种方式:每个节点仍然只存储一个数据,在查找插入位置的过程中,如果碰到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,即把这个新插入的数据当做大于这个节点的值来处理。
这样当要查找数据时,遇到值相同的节点,不通知查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。
删除操作,也需要先查找到每个要删除的节点,然后在按前面讲的删除操作的方法,依次删除。
8,二叉查找树的时间复杂度分析
二叉查找树的形态多种多样,每种的查找,插入,删除操作的执行效率都不一样。
但,不管操作是插入,删除还是查找,时间复杂度其实都根树的高度正比,即O(height)。
树的高度等于最大层数减一,每层包含的节点个数是2(k-1)。但对于完全二叉树,最后一层节点个数不遵守这个规律。它包含的节点个数在1个到2(L-1)个之间(假设最大层数是L)。
如果将每一层的节点数加起来就是总的节点个数n。则n满足以下关系:
n>=1+2+4+8+……+2^(L-2)+1
n<=1+2+4+8+……+2(L-2)+2(L-1)
得到L的范围是[log2(n+1),log2n +1]。
完全二叉树的层数小于等于log2^n + 1,即完全二叉树的高度小于等于log2^n
所以,极度不平衡的二叉查找树,它的查找性能肯定不能满足我们的需求。我们需要构建一种不管怎么删除,插入数据,在任何时候,都能保持任意节点左右子树都比较平衡的二叉查找树—平衡二叉查找树。
散列表无法替代二分查找树的原因:
1,散列表中的数据是无序存储的,若要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在O(n)的时间复杂度内,输出有序的数据序列。
2,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,在工程中常用的二叉查找树的性能非常稳定,时间复杂度稳定在O(logn。
3,笼统地讲,虽然散列表的查找操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个个常量不一定比logn小,所以实际查找速度可能不一定比O(logn)快。加上哈希函数的耗时,也不一定比平衡二叉查找树的效率高。
4,散列表的构造比二叉查找树要复杂,需要考虑的东西很多,如散列函数的设计,冲突解决办法,扩容,缩容等。而平衡二叉树只需要考虑平衡性这个一个问题,且这个问题的解决方案比较成熟,固定。
同时,为了避免过多的散列冲突,散列表的装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
C语言,完整的二叉查找树
#include
#include
/* A basic unbalanced binary search tree implementation in C, with the following functionalities implemented:
- Insertion
- Deletion
- Search by key value
- Listing of node keys in order of value (from left to right)
*/
// Node, the basic data structure in the tree
typedef struct node{
// left child
struct node* left;
// right child
struct node* right;
// data of the node
int data;
} node;
// The node constructor, which receives the key value input and returns a node pointer
node* newNode(int data){
// creates a slug
node* tmp = (node*)malloc(sizeof(node));
// initializes the slug
tmp->data = data;
tmp->left = NULL;
tmp->right = NULL;
return tmp;
}
// Insertion procedure, which inserts the input key in a new node in the tree
node* insert(node* root, int data){
// If the root of the subtree is null, insert key here
if (root == NULL)
root = newNode(data);
// If it isn't null and the input key is greater than the root key, insert in the right leaf
else if (data > root->data)
root->right = insert(root->right, data);
// If it isn't null and the input key is lower than the root key, insert in the left leaf
else if (data < root->data)
root->left = insert(root->left, data);
// Returns the modified tree
return root;
}
// Utilitary procedure to find the greatest key in the left subtree
node* getMax(node* root){
// If there's no leaf to the right, then this is the maximum key value
if (root->right == NULL)
return root;
else
root->right = getMax(root->right);
}
// Deletion procedure, which searches for the input key in the tree and removes it if present
node* delete(node* root, int data){
// If the root is null, nothing to be done
if (root == NULL)
return root;
// If the input key is greater than the root's, search in the right subtree
else if (data > root->data)
root->right = delete(root->right, data);
// If the input key is lower than the root's, search in the left subtree
else if (data < root->data)
root->left = delete(root->left, data);
// If the input key matches the root's, check the following cases
// termination condition
else if (data == root->data){
// Case 1: the root has no leaves, remove the node
if ((root->left == NULL) && (root->right == NULL)){
free(root);
return NULL;
}
// Case 2: the root has one leaf, make the leaf the new root and remove the old root
else if (root->left == NULL){
node* tmp = root;
root = root->right;
free(tmp);
return root;
}
else if (root->right == NULL){
node* tmp = root;
root = root->left;
free(tmp);
return root;
}
// Case 3: the root has 2 leaves, find the greatest key in the left subtree and switch with the root's
else {
// finds the biggest node in the left branch.
node* tmp = getMax(root->left);
// sets the data of this node equal to the data of the biggest node (lefts)
root->data = tmp->data;
root->left = delete(root->left, tmp->data);
}
}
return root;
}
// Search procedure, which looks for the input key in the tree and returns 1 if it's present or 0 if it's not in the tree
int find(node* root, int data){
// If the root is null, the key's not present
if (root == NULL)
return 0;
// If the input key is greater than the root's, search in the right subtree
else if (data > root->data)
return find(root->right, data);
// If the input key is lower than the root's, search in the left subtree
else if (data < root->data)
return find(root->left, data);
// If the input and the root key match, return 1
else if (data == root->data)
return 1;
}
// Utilitary procedure to measure the height of the binary tree
int height(node* root){
// If the root is null, this is the bottom of the tree (height 0)
if (root == NULL)
return 0;
else{
// Get the height from both left and right subtrees to check which is the greatest
int right_h = height(root->right);
int left_h = height(root->left);
// The final height is the height of the greatest subtree(left or right) plus 1(which is the root's level)
if (right_h > left_h)
return (right_h + 1);
else
return (left_h + 1);
}
}
// Utilitary procedure to free all nodes in a tree
void purge(node* root){
if (root != NULL){
if (root->left != NULL)
purge(root->left);
if (root->right != NULL)
purge(root->right);
free(root);
}
}
// Traversal procedure to list the current keys in the tree in order of value (from the left to the right)
void inOrder(node* root){
if(root != NULL){
inOrder(root->left);
printf("\t[ %d ]\t", root->data);
inOrder(root->right);
}
}
void main(){
// this reference don't change.
// only the tree changes.
node* root = NULL;
int opt = -1;
int data = 0;
// event-loop.
while (opt != 0){
printf("\n\n[1] Insert Node\n[2] Delete Node\n[3] Find a Node\n[4] Get current Height\n[5] Print Tree in Crescent Order\n[0] Quit\n");
scanf("%d",&opt); // reads the choice of the user
// processes the choice
switch(opt){
case 1: printf("Enter the new node's value:\n");
scanf("%d",&data);
root = insert(root,data);
break;
case 2: printf("Enter the value to be removed:\n");
if (root != NULL){
scanf("%d",&data);
root = delete(root,data);
}
else
printf("Tree is already empty!\n");
break;
case 3: printf("Enter the searched value:\n");
scanf("%d",&data);
find(root,data) ? printf("The value is in the tree.\n") : printf("The value is not in the tree.\n");
break;
case 4: printf("Current height of the tree is: %d\n", height(root));
break;
case 5: inOrder(root);
break;
}
}
// deletes the tree from the heap.
purge(root);
}