微信公众号:「Python读数」
如有问题或建议,请公众号留言
Seaborn是基于matplotlib的Python可视化库。 它提供了一个高级界面来绘制有吸引力的统计图形。Seaborn其实是在matplotlib的基础上进行了更高级的API封装,从而使得作图更加容易,不需要经过大量的调整就能使你的图变得精致。
Seaborn的安装
>>>pip install seaborn
安装完Seaborn包后,我们就开始进入接下来的学习啦,首先我们介绍kdeplot的画法。
注:所有代码均是在IPython notebook中实现
kdeplot(核密度估计图)
核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。具体用法如下:
*seaborn.kdeplot(data,data2=None,shade=False,vertical=False,kernel='gau',bw='scott',gridsize=100,cut=3,clip=None,legend=True,cumulative=False,shade_lowest=True,cbar=False, cbar_ax=None, cbar_kws=None, ax=None, *kwargs)
我们通过一些具体的例子来学习一些参数的用法:
首先导入相应的库
%matplotlib inline #IPython notebook中的魔法方法,这样每次运行后可以直接得到图像,不再需要使用plt.show()
import numpy as np #导入numpy包,用于生成数组
import seaborn as sns #习惯上简写成snssns.set()
sns.set()#切换到seaborn的默认运行配置
绘制简单的一维kde图像
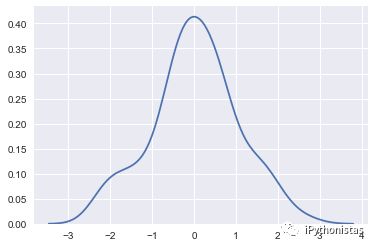
x=np.random.randn(100) #随机生成100个符合正态分布的数sns.kdeplot(x)
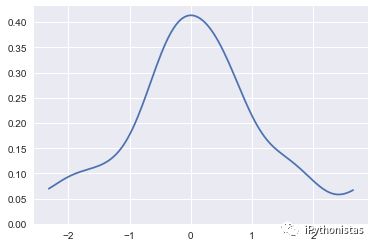
cut:参数表示绘制的时候,切除带宽往数轴极限数值的多少(默认为3)
sns.kdeplot(x,cut=0)
cumulative :是否绘制累积分布
sns.kdeplot(x,cumulative=True)
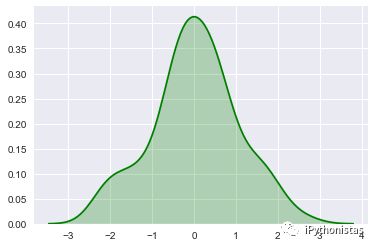
shade:若为True,则在kde曲线下面的区域中进行阴影处理,color控制曲线及阴影的颜色
sns.kdeplot(x,shade=True,color="g")
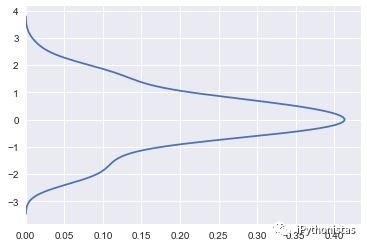
vertical:表示以X轴进行绘制还是以Y轴进行绘制
sns.kdeplot(x,vertical=True)
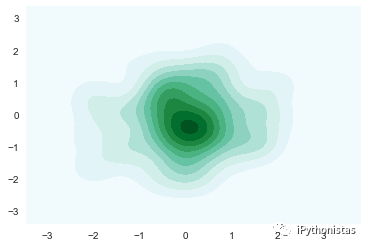
二元kde图像
y=np.random.randn(100)
sns.kdeplot(x,y,shade=True)
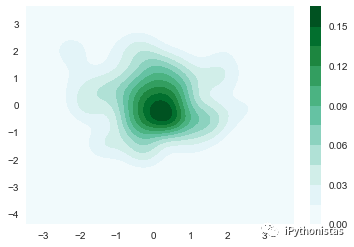
cbar:参数若为True,则会添加一个颜色棒(颜色帮在二元kde图像中才有)
sns.kdeplot(x,y,shade=True,cbar=True)
接下来,我们接着学习功能更为强大的distplot
distplot
displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。具体用法如下:
seaborn.distplot(a, bins=None, hist=True, kde=True, rug=False, fit=None, hist_kws=None, kde_kws=None, rug_kws=None, fit_kws=None, color=None, vertical=False, norm_hist=False, axlabel=None, label=None, ax=None)
先介绍一下直方图(Histograms):
直方图又称质量分布图,它是表示资料变化情况的一种主要工具。用直方图可以解析出资料的规则性,比较直观地看出产品质量特性的分布状态,对于资料分布状况一目了然,便于判断其总体质量分布情况。直方图表示通过沿数据范围形成分箱,然后绘制条以显示落入每个分箱的观测次数的数据分布。
接下来还是通过具体的例子来体验一下distplot的用法:
sns.distplot(x,color="g")
通过hist和kde参数调节是否显示直方图及核密度估计(默认hist,kde均为True)
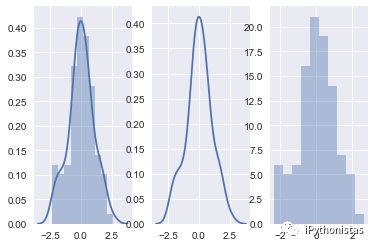
import matplotlib.pyplot as pltfig,axes=plt.subplots(1,3) #创建一个一行三列的画布
sns.distplot(x,ax=axes[0]) #左图
sns.distplot(x,hist=False,ax=axes[1]) #中图
sns.distplot(x,kde=False,ax=axes[2]) #右图
fig,axes=plt.subplots(1,2)
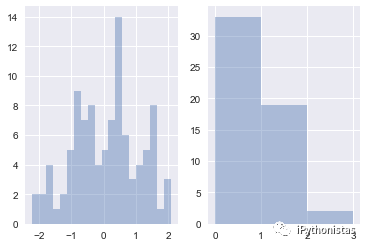
sns.distplot(x,kde=False,bins=20,ax=axes[0]) #左图:分成20个区间
sns.distplot(x,kde=False,bins=[x for x in range(4)],ax=axes[1]) #右图:以0,1,2,3为分割点,形成区间[0,1],[1,2],[2,3],区间外的值不计入。
rag:控制是否生成观测数值的小细条
fig,axes=plt.subplots(1,2)
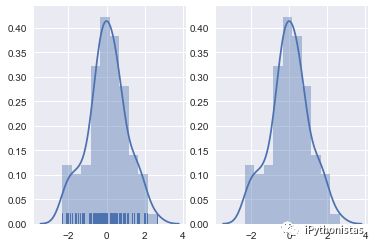
sns.distplot(x,rug=True,ax=axes[0]) #左图
sns.distplot(x,ax=axes[1]) #右图
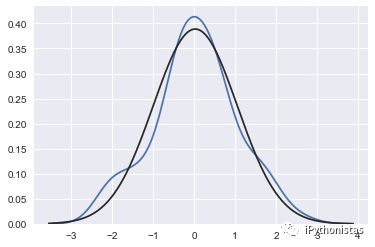
fit:控制拟合的参数分布图形,能够直观地评估它与观察数据的对应关系(黑色线条为确定的分布)
from scipy.stats import *
sns.distplot(x,hist=False,fit=norm) #拟合标准正态分布
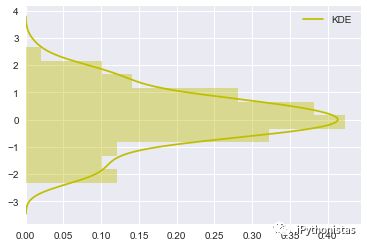
hist_kws, kde_kws, rug_kws, fit_kws参数接收字典类型,可以自行定义更多高级的样式
sns.distplot(x,kde_kws={"label":"KDE"},vertical=True,color="y")
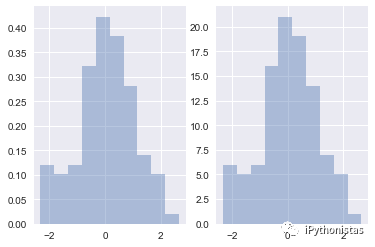
norm_hist:若为True, 则直方图高度显示密度而非计数(含有kde图像中默认为True)
fig,axes=plt.subplots(1,2)
sns.distplot(x,norm_hist=True,kde=False,ax=axes[0]) #左图
sns.distplot(x,kde=False,ax=axes[1]) #右图
还有其他参数就不在此一一介绍了,有兴趣继续深入学习的同学可以查看Seaborn的官方文档。以上内容是我结合官方文档和自己的一点理解写成的,有什么错误大家可以指出来并提提意见,共同交流、进步,也希望我写的这些能够给阅读完本文的你或多或少带来一点帮助!
关注我的公众号「Python读数」,后台回复「py」即可获取Python学习资源礼包,还有Python学习交流群哦!